什麼是貝葉斯思維？ 引言與定理

英國統計學家和哲學家托馬斯·貝葉斯在 1700 年代給出的統計定理仍然是世界各地科學家和分析師的指路明燈。 今天，貝葉斯思想在醫學、科學、技術和其他幾個學科中得到應用，並繼續強烈影響我們的世界觀和由此產生的行動。

托馬斯的貝葉斯想法非常簡單。 根據貝葉斯，假設成立的概率取決於兩個條件：它基於我們已經知道的（先驗知識）的合理程度以及它與新證據的匹配程度。 因此，貝葉斯思維不同於傳統的假設檢驗，因為前者在得出結論之前包括先驗知識。

考慮到初步介紹，讓我們深入了解貝葉斯統計的更多細節。

貝葉斯統計

簡單來說，貝葉斯統計將概率應用於統計問題，以根據新數據的證據更新先前的信念。 概率表示對特定事件的相信程度。

相信程度可以基於基於個人假設或先前實驗結果的關於事件的先前知識。 貝葉斯統計使用貝葉斯定理來計算概率。 反過來，貝葉斯定理描述了基於新證據和與事件相關的先驗信息的事件的條件概率。

考慮到這一點，在深入理解貝葉斯定理之前，讓我們複習一下條件概率的基本概念。

條件概率

條件概率可以定義為基於先前事件或結果發生的事件或結果的可能性。 它是通過將先前事件的概率乘以後續或條件事件的概率來計算的。

讓我們看一個例子來更好地理解這個概念。

• 事件A是計劃外出野餐。 這家人有 80% 的機會去野餐。
• 事件B是一家人出去野餐的那天會下雨。 天氣預報說野餐當天有 60% 的概率會下雨。
• 因此，家庭去野餐並且下雨的概率（P）計算如下：

P（野餐和雨）= P（雨|野餐）P（野餐）= (0.60) * (0.80) = 0.48

在上面的例子中，條件概率著眼於兩個事件 A 和 B 的相互關係，即家人去野餐並且同一天也下雨的概率。

因此，條件概率與無條件概率不同，因為後者指的是事件發生的可能性，無論是否發生任何其他事件或事件或是否存在任何其他條件。

條件概率的公式

條件概率的公式來自概率乘法規則：

P (A 和 B) 或 P (AUB) = P ( B 給定 A) 或 P (B | A) * P (A)

上式中，P（A和B）是聯合概率，指的是兩個或多個事件同時發生的可能性。 它也寫成 P(A,B)。

下面是如何從乘法規則推導出條件概率方程：

第一步：寫下乘法規則。

P (A 和 B) = P (B | A) * P (A)

第 2 步：將等式兩邊除以 P (A)。

P (A 和 B) / P (A) = P (B | A) * P (A) / P (A)

第三步：取消等式右邊的P(A)。

P (A 和 B) / P (A) = P (B | A)

第 4 步：重寫方程。

P (A 和 B) = P (B | A) / P (A)

因此，條件概率的公式如下：

P (A 和 B) = P (B | A) / P (A)

貝葉斯定理

使用貝葉斯定理，我們可以根據新的相關證據更新我們的信念和信念。 例如，如果我們試圖計算某個人患癌症的概率，我們通常會假設它是患癌症的人口百分比。 但是，如果我們引入額外的證據，例如所討論的人是一個經常吸煙的人，我們可以更新我們的看法（以及因此概率），因為如果一個人是吸煙者，患癌症的概率會更高。 因此，我們利用我們的先驗知識和額外的證據來改進我們的估計。

貝葉斯定理的公式

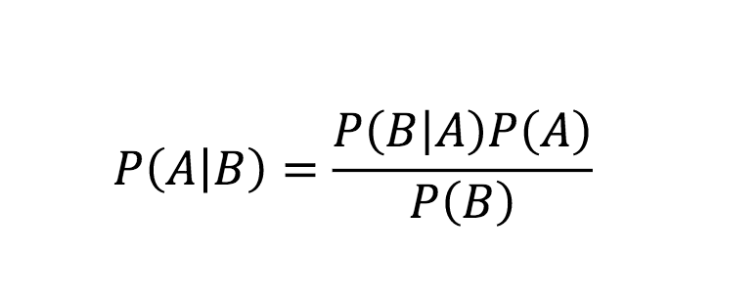
資源

上述等式是貝葉斯規則。 現在，讓我們看看貝葉斯定理方程的逐步推導。

第 1 步：考慮兩個事件，A 和 B。A 是我們要計算其概率的事件，B 是與 A 相關的附加證據。

第二步：寫出事件 A 和 B 的聯合概率和條件概率之間的關係。

P (A,B) = P (A | B) * P(B) = P (B,A) = P (B | A) * P(A)

第三步：設置兩個條件概率項相等。

P (A | B) * P(B) = P (B | A) * P(A)

第 4 步：將等式兩邊除以 P (B)。

P (A | B) * P(B) / P (B) = P (B | A) * P(A) / P (B)

步驟 5：取消等式左側的 P (B)。

P (A | B) = P (B | A) * P(A) / P (B)

因此，我們得到貝葉斯定理的公式如下：

P (A | B) = P (B | A) * P(A) / P (B)

理解貝葉斯定理方程中的項

P (A | B) = P (B | A) * P(A) / P (B)

• P (A | B)稱為後驗概率或我們試圖估計的概率。 基於前面的例子，後驗概率將是這個人患有癌症的概率，假設這個人是一個經常吸煙的人。
• P (B | A)被稱為似然性，指的是在給定我們初始假設的情況下檢測到額外證據的概率。 在上面的例子中，可能性是這個人是吸煙者的概率，假設這個人患有癌症。
• P (A)是先驗概率或我們假設的概率，沒有任何額外的證據或信息。 在上面的例子中，先驗概率是患癌症的概率。
• P (B)是觀察證據的邊際可能性或總概率。 在上述示例的上下文中，邊際可能性是吸煙者的概率。

一個簡單的例子來理解貝葉斯定理

使用前面示例中的一些假設數字，我們將看到應用貝葉斯定理的效果。

假設得癌症的概率是0.06，即6%的人得癌症。 現在，假設成為吸煙者的概率是 0.20 或 20% 的人是吸煙者，30% 的癌症患者是吸煙者。 因此，P（吸煙者 | 癌症）= 0.30。

最初，患癌症的概率僅為 0.06（之前）。 但是使用新的證據，我們可以計算出 P (Cancer | Smoker) = P ((Smoker | Cancer) * P (Cancer)) / P (Smoker) = (0.30*0.06) / (0.20) = 0.09。

從世界頂級大學在線學習數據科學課程。 獲得行政 PG 課程、高級證書課程或碩士課程，以加快您的職業生涯。

前進之路：掌握數據科學或機器學習職業的統計概念

upGrad 的高等教育技術學習平台以其豐富的課程和沈浸式學習體驗影響了全球超過 500,000 名在職專業人士。 upGrad 的行業相關課程在 85 多個國家/地區擁有 40,000 多名學習者，保證能在您選擇的領域推動您的職業發展。

數據科學理學碩士課程為期 18 個月，傳授統計、預測分析、機器學習、大數據分析、數據可視化等方面的關鍵技能。

節目亮點：

• 利物浦約翰摩爾斯大學碩士學位和班加羅爾 IIIT 執行 PGP
• 500 多個小時的內容、60 多個案例研究和項目、20 多個現場會議、14 多種編程語言和工具
• 行業網絡、疑難解答會議和學習支持

機器學習和深度學習高級證書課程是一門為期 6 個月的嚴格課程，提供同行交流機會、實踐項目、行業指導和 360 度職業幫助。

節目亮點：

• 來自 IIIT 班加羅爾的聲望認可
• 240 多個小時的內容，5 個以上的案例研究和項目，24 多個現場會議，涵蓋 12 種編程語言、工具和庫
• 1:8 小組輔導課程和 1:1 行業專家輔導課程

結論

貝葉斯思維支撐著人類思維、探究和信念的幾個領域，儘管我們大多數人都沒有意識到這一點。 從癌症篩查和全球變暖到貨幣政策和風險評估和保險，貝葉斯思維是基礎。 即使是著名的英國數學家艾倫·圖靈也被認為在第二次世界大戰期間採用貝葉斯方法破解了德國的謎密碼。

註冊 upGrad並進一步了解關鍵統計概念等等！