數據結構中的樹：每個數據科學家都應該知道的 8 種樹

介紹

在計算領域，數據結構是指數據在磁盤上的排列方式，便於存儲和顯示。 它們屬於數據科學領域，預計該領域將成為 2021 年有利可圖的職業選擇。基於對未來幾年的預測，大規模深度學習模型和下一代智能設備將為未來這個部門。

因此，獲得數據結構的知識對於在技術進步中找到合適的職業至關重要。 根據 2021 年數據科學行業的預測，美國和印度將在其 2,50,000 多家公司中僱傭大約 50,000 名數據科學家和 300,000 名數據分析師。 [1]

數據結構用於設計信息分配、管理和檢索的路徑。 數據結構對於起草和提高整體處理數據的效率尤其必要。 他們通過對數據進行分組和組織來管理數據，以有效地促進信息交換。

數據結構中的樹

“樹”是一種 ADT（抽像數據類型），其數據分配遵循分層模式。 本質上，樹是通過邊連接的多個節點的集合。 這些“樹”形成了類似於樹的數據結構設計，其中“根”節點通向“父”節點，最終通向“子”節點。 連接是用稱為“邊緣”的線進行的。

“葉子”節點是沒有其他子節點源自它們的端點。 由於其排列的非線性特性，數據結構中的樹起著至關重要的作用。 這可以在搜索期間實現更快的響應時間，並在整個設計階段提供便利。

數據結構中的樹類型

下面深入解釋數據結構中的各種類型的樹：

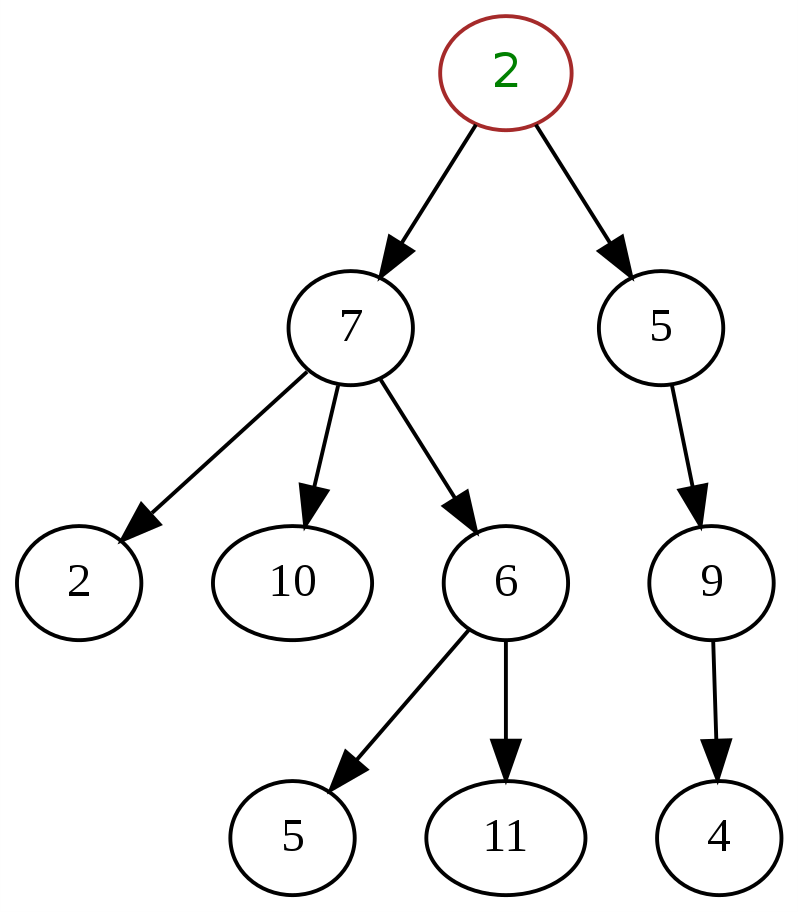
1. 一般樹

一般樹的特點是對節點可以擁有的子節點數量沒有任何規範或限制。 任何具有層次結構的樹都可以歸類為一般樹。 一個節點可以有多個子節點，並且樹的方向可以有任何類型的組合。 節點可以是任何度數，從 0 到 n。

以下是數據結構中通用樹的經典示例，頂部的“2”是根節點。

資源

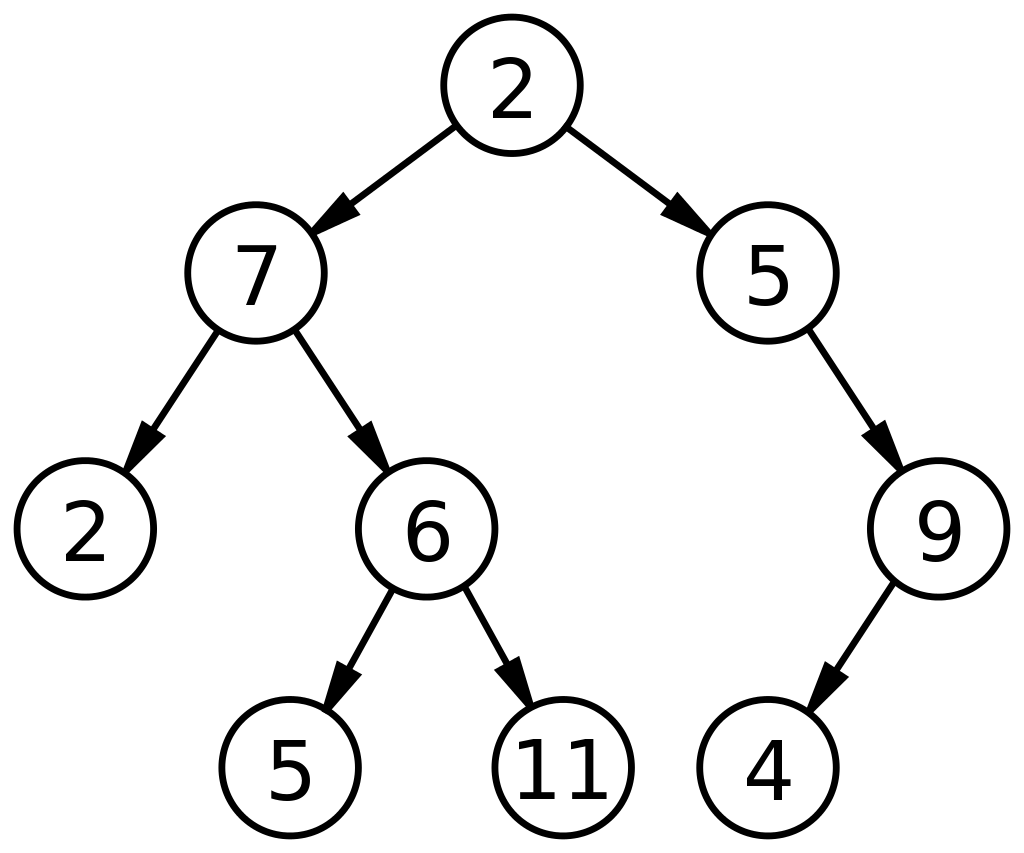
2. 二叉樹

正如“二進制”一詞所定義的那樣，這意味著兩個數字，二叉樹由可以具有 2 個子節點的節點組成。 二叉樹中的任何節點最多可以有 0、1 或 2 個節點。 數據結構中的二叉樹是功能強大的 ADT，可以進一步細分為多種類型。 它們主要用於數據結構中，有兩個目的：

1. 用於訪問節點並標記它們，如二叉搜索樹中所觀察到的。
2. 用於通過分叉結構表示數據。

下面是數據結構中二叉樹的基本圖：

資源

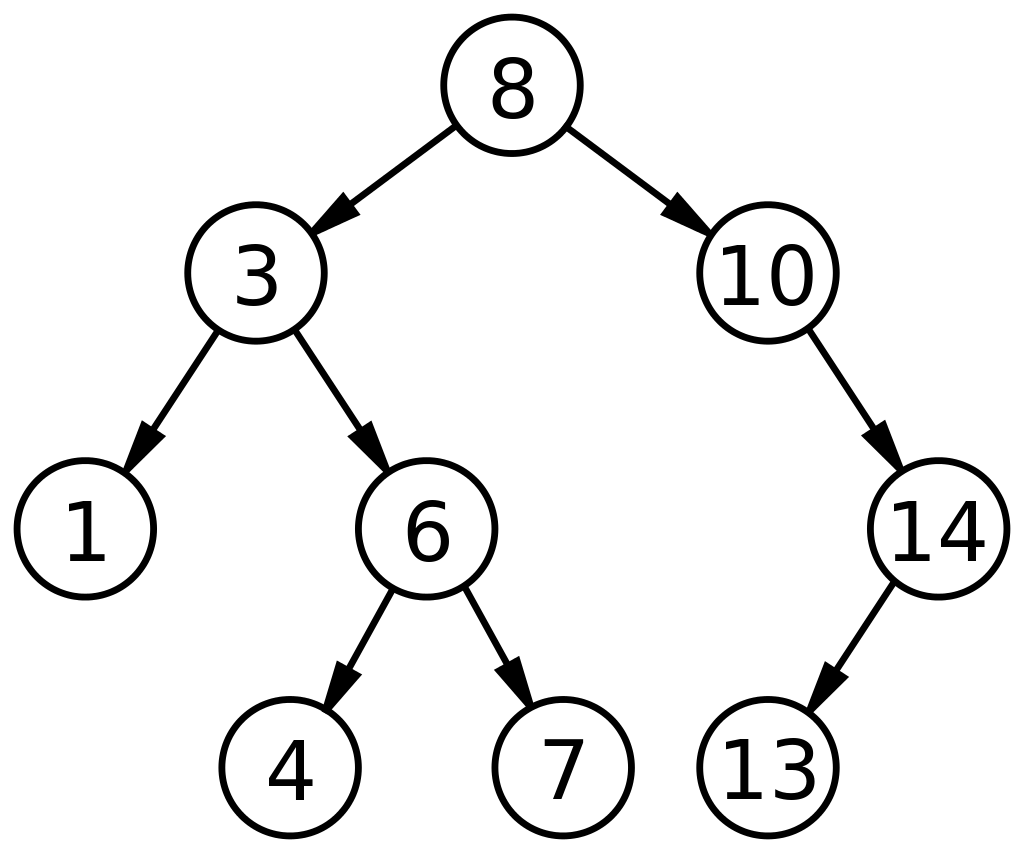
3. 二叉搜索樹

二叉搜索樹 (BST) 是二叉樹的一種獨特子類型，其排列方式有助於更快地搜索/查找或添加/刪除數據。 BST 由基於三個字段的節點表示定義：數據、其左孩子和右孩子。 BST 的控制因素是：

1. 左側的每個節點（左子節點）的值都必須小於其父節點。
2. 右側的每個節點（右子節點）的值都必須高於其父節點。

這種佈置將搜索時間減少到線性搜索的一半，如在數組中發現的那樣。 因此，與其他 ADT 相比，數據結構中的二叉搜索樹廣泛適用於搜索和排序。

資源

儘管 BT 和 BST 本質上都是數據結構中的樹，但不要被它們名稱的相似性所迷惑。 在 upGrad 上詳細了解二叉樹和二叉搜索樹之間的區別。

4.AVL樹

AVL 樹的名字來源於它的發明者：Adelson-Velsky 和 ​​Landis。 AVL 樹的特點是具有自平衡特性。 其根節點的兩個子樹的高度限制為小於兩個。 當高度差增加到 1 以上時，子節點會重新平衡。

AVL 樹是高度平衡的，這種重新平衡通過單次或雙次旋轉發生。 平衡因子是左子樹和右子樹的高度之差，取值為-1、0、1。

5. 紅黑樹

這種類型類似於 AVL 樹，因為紅黑樹也是高度平衡的。 它們的不同之處在於它不需要超過兩次旋轉來平衡它們。 它們包含一個額外的位，用於定義節點的紅色或黑色，以確保在刪除和插入期間樹是平衡的。 在更改期間也會重新繪製紅黑色編碼，但幾乎沒有額外的內存成本。

6.張開樹

二叉搜索樹的另一個子類型，展開樹，具有執行旋轉操作以調整最近節點的獨特屬性。 最近訪問的節點通過旋轉排列為根節點。 它是一棵平衡的樹，但不是高度平衡的樹。

“展開”的動作是在初始二叉樹搜索之後執行的，因為樹的旋轉是以特定的方式執行的。 每次操作後，樹都會旋轉以平衡自身，並將搜索到的元素作為根節點排列在頂部。

7. 陷阱

數據結構中的“Treaps”是樹和堆的組合。 在 BST 中，左孩子的值必須小於根節點，而右孩子的值必須高於根節點。 在堆數據結構中，根節點的值最小，其子節點（左右）具有較大的值。

因此，treap 以鍵（類似於 BST）和優先級（如堆）的形式保存值。 優先級最高的節點首先插入到二叉搜索樹中，優先級數是獨立的隨機數。 它們維護一組動態的有序鍵，並允許在它們的鍵中進行二進制搜索。

8. B樹

作為數據結構中的一種自平衡樹，B-Tree 對數據進行排序以允許在對數時間內進行搜索、順序訪問、刪除和插入。 與二叉樹不同，B 樹允許其節點有兩個以上的子節點。 它們與讀取和寫入更大數據塊的數據庫和文件系統兼容。

數據結構中的 B 樹用於較大的存儲系統，例如磁盤。 所有的葉子都沒有任何信息，它們出現在同一層次內。 B 樹的內部節點可以具有由范圍限制的可變大小的子節點。

這些是數據結構中的樹，由設計數據流的程序員實現。 了解它們的獨特特徵和應用對於您成為數據科學家的旅程至關重要。 另一種提高自己技能的方法是通過各種需要了解數據結構中的樹和其他形式的 ADT 知識的項目進行練習。

為了將您的知識應用於 DS 項目，以下博客鏈接為初學者提供了 13 個有趣的數據結構項目想法和主題 [2021] 。

結論

學習數據結構中的樹之類的概念可能會很棘手，而有志於編程的人需要專家指導來自學。 要了解有關數據結構中樹的更多信息，請查看upGrad的在線課程。 軟件開發執行 PG 計劃 – IIIT-B 和 upGrad 的 DevOps 專業化 DevOps 可以幫助您建立自己的程序員職業生涯。

由於數據結構的熟練程度是編碼過程不可或缺的一部分，因此它可以幫助學生成為專家級程序員和軟件開發人員。 在未來的幾十年裡，程序員和數據科學家必將受到需求。

我們在印度有 5 億互聯網用戶，產生和消費大量數據，需要雇傭數千名數據科學家來滿足需求。 [2]這些數據科學家需要適當的教育和相關的技術專長，才能在該領域尋找工作。

由upGrad和 IIIT-Bangalore 策劃的軟件開發執行 PG 計劃 - 全棧開發專業化，可以幫助您提高個人資料並獲得更好的程序員就業機會。