負二項式回歸入門:分步指南
已發表: 2022-04-17負二項式回歸技術用於對計數變量進行建模。 該方法與多元回歸方法幾乎相似。 但是,在負二項式回歸的情況下,因變量(即 Y)遵循負二項式分佈存在差異。 因此,變量的值可以是非負整數,例如 0、1、2。
該方法也是泊松回歸的擴展,它在假設均值等於方差時放寬了。 二項式回歸的傳統模型之一,定義為“NB2”,是基於泊松伽馬的混合分佈。
泊松回歸的方法是通過添加一個伽馬噪聲變量來推廣的。 這個變量的值是平均值,還有一個比例參數是“v”。
以下是負二項式回歸的一些示例:
- 學校管理人員進行了一項研究,以研究兩所學校的高中生的出勤行為。 可能影響出勤行為的因素可能包括大三學生缺課的天數。 此外,他們註冊的計劃。
- 來自一項健康相關研究的研究人員對過去 12 個月內有多少老年人到訪醫院進行了研究。 該研究基於個人特徵和老年人購買的健康計劃。
負二項式回歸示例
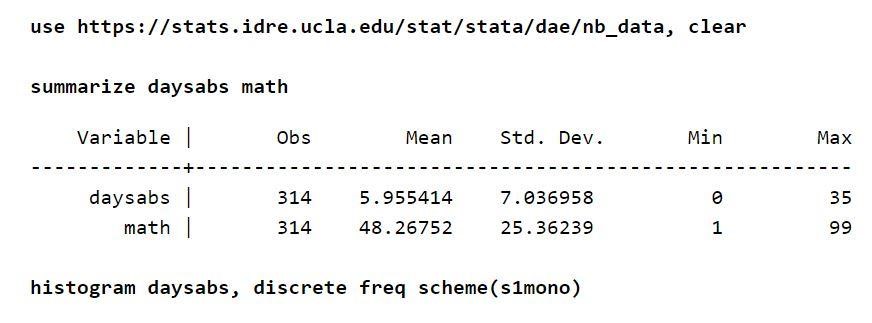
假設有大約 314 名高中學生的出勤表。 數據取自兩所城市學校,並存儲在名為 nb_data.dta 的文件中。 此示例中有趣的響應變量是缺席天數,即“daysabs”。 存在一個變量“數學”,它定義了每個學生的數學分數。 還有另一個變量是“prog”。 該變量表示學生註冊的課程。
資源

每個變量都有大約 314 個觀測值。 因此,變量之間的分佈也是合理的。 此外,考慮到結果變量,無條件均值低於方差。
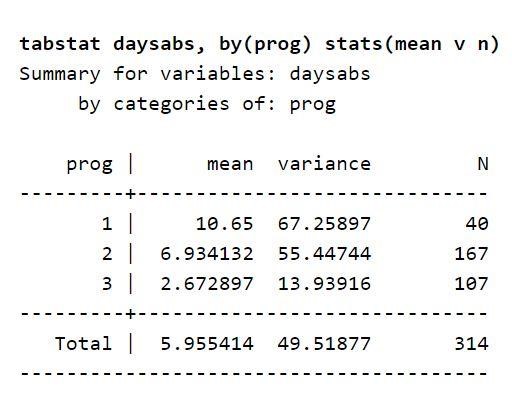
現在,關注數據集中考慮的變量描述。 一個表格列出了學生在每種課程類型中的平均缺勤天數。 這表明變量類型程序可以預測學生缺課的天數。 您也可以使用它來預測結果變量。 這是因為結果變量的平均值因變量 prog 而異。 此外,方差的值高於變量 prog 的每個級別中的值。 這些值稱為方差和均值。 現有差異表明存在過度分散,因此使用負二項式模型是合適的。
資源
研究人員可以為此類研究考慮多種分析方法。 這些方法如下所述。 用戶可用於分析回歸模型的一些分析方法是:
1. 負二項式回歸
當存在過度分散的數據時,將使用負二項式回歸方法。 這意味著條件方差的值高於或超過條件均值的值。 該方法被認為是從泊松回歸方法推廣而來的。 這是因為這兩種方法的均值結構相同。 但是,負二項式回歸中有一個附加參數用於對過度離散進行建模。 當條件分佈與結果變量過度分散時,置信區間被認為比激情回歸更窄。
2.泊松回歸
泊松回歸的方法用於計數數據的建模。 許多擴展可用於對泊松回歸中的計數變量進行建模。
3.OLS回歸
計數變量的結果有時會進行對數變換,然後通過 OLS 回歸方法進行分析。 但是,有時存在與 OLS 回歸方法相關的問題。 這些問題可能是由於通過考慮零值的對數生成任何未定義值而導致的數據丟失。 此外,它可能是由於缺乏對分散數據的建模而產生的。
4.零膨脹模型
這些類型的模型試圖解釋模型中所有多餘的零。
使用負二項式回歸分析
命令“nbreg”用於估計負二項式回歸模型。 變量“prog”之前有一個“i”。 “i”的存在表明該變量是類型因子,即分類變量。 這些應作為指標變量包含在模型中。

- 模型的輸出以迭代日誌開始。 它從泊松模型的擬合開始,然後是零模型,然後是負二項式模型。 該方法使用最大似然估計並不斷迭代,直到最終對數的值發生變化。 對數的可能性用於模型的比較。
- 下一個信息在頭文件中。
- 標題下方有負二項式回歸係數的信息。 為每個變量生成係數以及 p 值、z 分數等誤差。 所有係數的置信區間也為 95%。 “數學”變量的係數為 -0.006,表示它具有統計顯著性。 結果意味著,如果變量“math”增加一個單位,則缺席天數的預期日誌計數將減少 0.006 的值。 此外,指示變量 2. prog 的值是兩組(組 2 和參考組)之間日誌計數的預期差異。
- 對日誌傳輸過度分散的參數估計已完成,然後以未轉換的值顯示。 在泊松模型中,該值為零。
- 係數表下方有一個比率檢驗似然信息。 通過使用“margins”命令可以進一步理解該模型。
在 Python 中進行負二項式回歸分析的過程
執行回歸過程所需的包需要從 Python 中導入。 下面列出了這些軟件包:
- 將 statsmodels.api 導入為 sm
- 將 matplotlib.pyplot 導入為 plt
- 將 numpy 導入為 np
- 從 patsy 導入 dmatrices
- 將熊貓導入為 pd
負二項式回歸的注意事項
在應用負二項式回歸分析方法時,應考慮一些事項。 這些包括:

- 如果存在小樣本,則不推薦使用負二項回歸方法。
- 有時存在過多的零點,這可能是過度分散的原因。 由於添加數據生成的過程,可能會生成這些零。 如果出現此類情況,建議使用零膨脹模型的方法。
- 如果數據生成過程不考慮任何零點,那麼在這種情況下,建議使用零截斷模型的方法。
- 有一個與計數數據相關的曝光變量。 該變量表示事件可能發生的時間。 這個變量是必須納入負二項式回歸模型的。 這是通過 exp() 的選項來完成的。
- 結果變量不能是負二項式回歸分析模型中的任何負值。 此外,曝光變量的值不能為 0。
- 命令“glm”也可用於運行負二項式回歸分析方法。 這可以通過日誌的鏈接以及二項式系列來完成。
- 獲取殘差需要命令“glm”。 這是為了檢查負二項式回歸模型中是否還有其他假設。
- 存在偽 R 平方的各種度量。 但是,每個度量都提供類似於 OLS 回歸中 R 平方提供的信息的信息。
結論
文章討論了負二項式回歸這個話題。 我們已經看到,它幾乎類似於多元回歸的方法,是泊松分佈的一種廣義形式。 該方法有多種應用。 該技術也可以通過 python 編程語言或 R 應用。
一些案例研究也展示了它在衰老等研究中的應用。 此外,可用於計數數據的經典回歸模型是泊松回歸、負二項式回歸和幾何回歸。 這些方法屬於線性模型家族,幾乎包含在所有統計軟件包中,例如 R 系統。
如果您想在機器學習方面表現出色並想探索數據領域,那麼您可以查看 upGrad 提供的機器學習和人工智能中的 Executive PG Program 課程。 因此,如果您是一名夢想成為機器學習專家的工作專業人士,請來獲得在專家手下接受培訓的經驗。 更多細節可以通過我們的網站獲得。 如有任何疑問,我們的團隊可以及時為您提供幫助。