你應該知道的 7 個 Python 中最常用的機器學習算法

機器學習是人工智能 (AI) 的一個分支，它處理用於任何數據的計算機算法。 它專注於從輸入的數據中自動學習，並通過每次改進先前的預測來為我們提供結果。

Python 中使用的頂級機器學習算法

以下是 Python 中使用的一些頂級機器學習算法，以及代碼片段顯示了它們的實現和分類邊界的可視化。

1. 線性回歸

線性回歸是最常用的監督機器學習技術之一。 顧名思義，此回歸嘗試使用線性方程對兩個變量之間的關係進行建模，並將該線擬合到觀察到的數據。 該技術用於估計真實的連續值，例如總銷售額或房屋成本。

最佳擬合線也稱為回歸線。 它由以下等式給出：

Y = a*X + b

其中 Y 是因變量，a 是斜率，X 是自變量，b 是截距值。 係數 a 和 b 是通過最小化各個數據點與回歸線方程之間的距離差的平方得出的。

# 用於簡單回歸的合成數據集

從 sklearn.datasets 導入 make_regression

plt.figure()

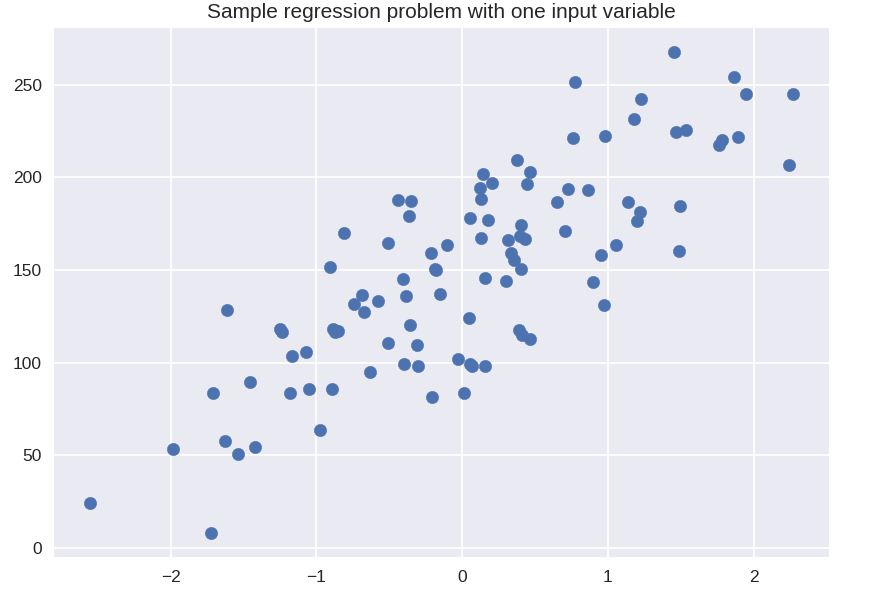
plt.title('一個輸入變量的樣本回歸問題')

X_R1，y_R1 = make_regression（n_samples = 100，n_features = 1，n_informative = 1，偏差 = 150.0，噪聲 = 30，random_state = 0）

plt.scatter(X_R1, y_R1, 標記 = 'o', s = 50)

plt.show()

從 sklearn.linear_model 導入線性回歸

X_train，X_test，y_train，y_test = train_test_split（X_R1，y_R1，

隨機狀態 = 0)

linreg = LinearRegression().fit(X_train, y_train)

print('線性模型係數 (w): {}'.format(linreg.coef_))

print('線性模型截距(b): {:.3f}'z.format(linreg.intercept_))

print('R-squared score (training): {:.3f}'.format(linreg.score(X_train, y_train)))

print('R-squared score (test): {:.3f}'.format(linreg.score(X_test, y_test)))

輸出

線性模型係數（w）：[45.71]

線性模型截距（b）：148.446

R平方分數（訓練）：0.679

R平方分數（測試）：0.492

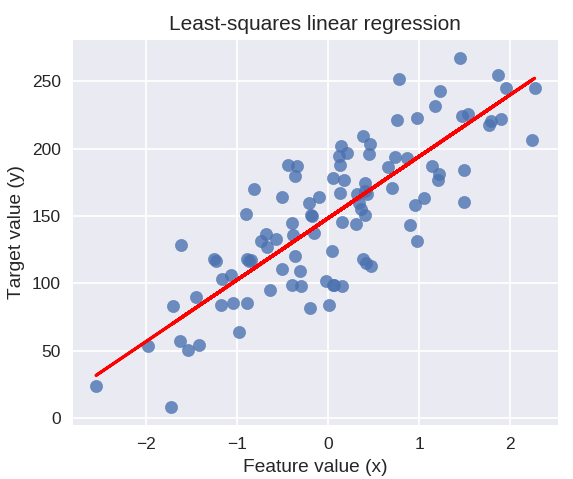
以下代碼將在我們的數據點圖上繪製擬合回歸線。

plt.figure(figsize = (5, 4))

plt.scatter(X_R1, y_R1, marker = 'o', s = 50, alpha = 0.8)

plt.plot(X_R1, linreg.coef_ * X_R1 + linreg.intercept_, 'r-')

plt.title('最小二乘線性回歸')

plt.xlabel('特徵值(x)')

plt.ylabel('目標值(y)')

plt.show()

準備用於探索分類技術的通用數據集

以下數據將用於展示 Python 機器學習中最常用的各種分類算法。

UCI 蘑菇數據集存儲在蘑菇.csv 中。

%matplotlib 筆記本

將熊貓導入為 pd

將 numpy 導入為 np

將 matplotlib.pyplot 導入為 plt

從 sklearn.decomposition 導入 PCA

從 sklearn.model_selection 導入 train_test_split

df = pd.read_csv('readonly/mushrooms.csv')

df2 = pd.get_dummies(df)

df3 = df2.sample(frac = 0.08)

X = df3.iloc[:, 2:]

y = df3.iloc[:, 1]

pca = PCA（n_components = 2）.fit_transform（X）

X_train，X_test，y_train，y_test = train_test_split（pca，y，random_state = 0）

plt.figure(dpi = 120)

plt.scatter(pca[y.values == 0, 0], pca[y.values == 0, 1], alpha = 0.5, label = 'Edible', s = 2)

plt.scatter(pca[y.values == 1, 0], pca[y.values == 1, 1], alpha = 0.5, label = 'Poisonous', s = 2)

plt.legend()

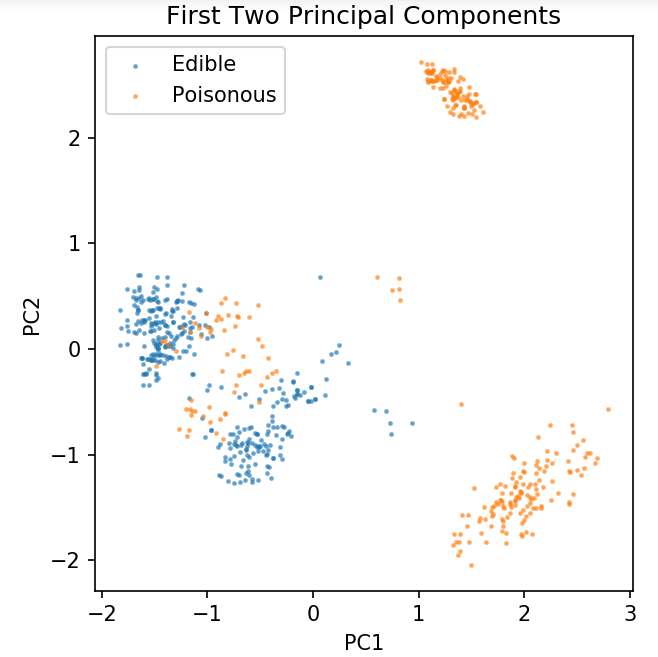
plt.title('蘑菇數據集\n前兩個主成分')

plt.xlabel('PC1')

plt.ylabel('PC2')

plt.gca().set_aspect('等於')

我們將使用下面定義的函數來獲取我們將在蘑菇數據集上使用的不同分類器的決策邊界。

def plot_mushroom_boundary（X，y，fitted_model）：

plt.figure(figsize = (9.8, 5), dpi = 100)

對於 i，枚舉中的 plot_type（['Decision Boundary'，'Decision Probabilities']）：

plt.subplot( 1, 2, i + 1 )

mesh_step_size = 0.01 # 網格中的步長

x_min, x_max = X[:, 0].min() – .1, X[:, 0].max() + .1

y_min, y_max = X[:, 1].min() – .1, X[:, 1].max() + .1

xx，yy = np.meshgrid（np.arange（x_min，x_max，mesh_step_size），np.arange（y_min，y_max，mesh_step_size））

如果我 == 0：

Z = 擬合模型預測（np.c_[xx.ravel(), yy.ravel()] ）

別的：

嘗試：

Z = 擬合模型.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]

除了：

plt.text(0.4, 0.5, '概率不可用', 水平對齊 = '中心', 垂直對齊 = '中心', 變換 = plt.gca().transAxes, fontsize = 12)

plt.axis('關閉')

休息

Z = Z.reshape(xx.shape)

plt.scatter(X[y.values == 0, 0], X[y.values == 0, 1], alpha = 0.4, label = 'Edible', s = 5)

plt.scatter(X[y.values == 1, 0], X[y.values == 1, 1], alpha = 0.4, label = 'Posionous', s = 5)

plt.imshow（Z，插值='最近'，cmap ='RdYlBu_r'，alpha = 0.15，範圍=（x_min，x_max，y_min，y_max），原點='下'）

plt.title(plot_type +'\n'+str(fitted_model).split('(')[0]+'測試精度：'+str(np.round(fitted_model.score(X,y),5)) )

plt.gca().set_aspect('等於');

plt.tight_layout()

plt.subplots_adjust（頂部 = 0.9，底部 = 0.08，wspace = 0.02）

2. 邏輯回歸

與線性回歸不同，邏輯回歸處理離散值的估計（0/1 二進制值、真/假、是/否）。 這種技術也稱為 logit 回歸。 這是因為它通過使用 logit 函數來訓練給定數據來預測事件的概率。 它的值始終介於 0 和 1 之間（因為它正在計算概率）。

結果的對數機率構造為預測變量的線性組合，如下所示：

機率 = p / (1 – p) = 事件發生的概率或事件不發生的概率

ln( 賠率 ) = ln( p / (1 – p) )

logit( p ) = ln( p / (1 – p) ) = b0 + b1X1 + b2X2 + b3X3 + … + bkXk

其中 p 是特徵存在的概率。

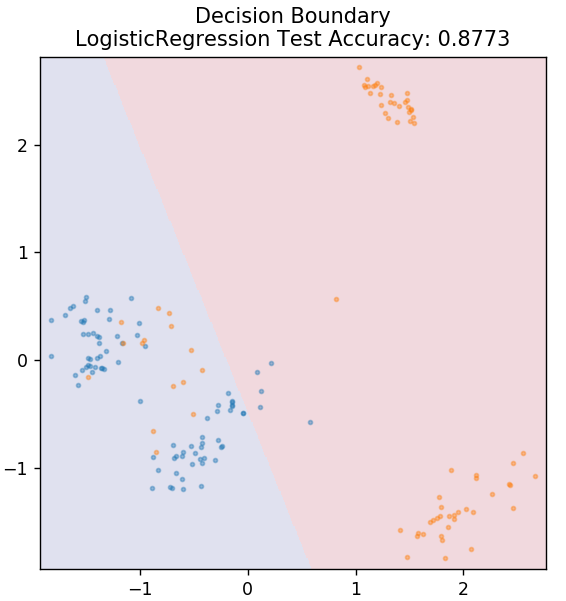
從 sklearn.linear_model 導入 LogisticRegression

模型 = 邏輯回歸（）

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

從世界頂級大學在線獲得人工智能認證——碩士、高級管理人員研究生課程和 ML 和 AI 高級證書課程，以加快您的職業生涯。

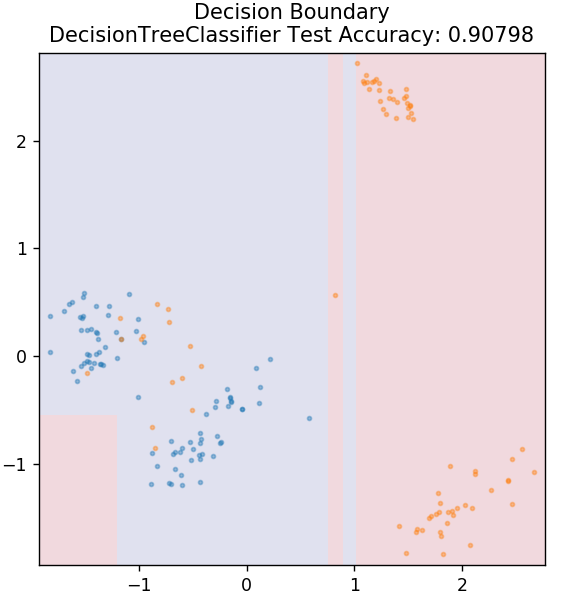
3. 決策樹

這是一種非常流行的算法，可用於對數據的連續變量和離散變量進行分類。 在每一步，數據都會根據一些拆分屬性/條件拆分為多個同質集。

從 sklearn.tree 導入 DecisionTreeClassifier

模型 = 決策樹分類器（最大深度 = 3）

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

4. 支持向量機

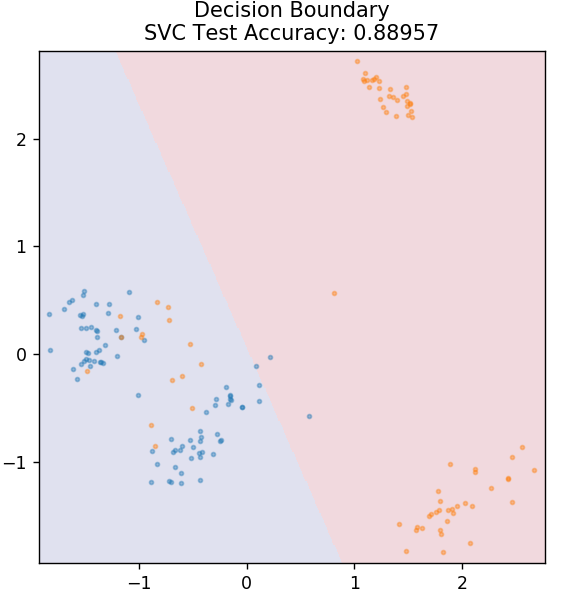
SVM 是支持向量機的縮寫。 這裡的基本思想是通過使用超平面進行分離來對數據點進行分類。 目標是找出在類或類別的數據點之間具有最大距離（或邊距）的超平面。

我們選擇平面的方式是為了在未來以最高的置信度對未知點進行分類。 支持向量機的使用非常著名，因為它們提供了高精度，同時佔用的計算能力非常少。 SVM 也可用於回歸問題。

從 sklearn.svm 導入 SVC

模型= SVC（內核='線性'）

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

結帳： GitHub 上的 Python 項目

5.樸素貝葉斯

顧名思義，樸素貝葉斯算法是一種基於貝葉斯定理的監督學習算法。 貝葉斯定理使用條件概率根據給定的知識為您提供事件的概率。

在哪裡，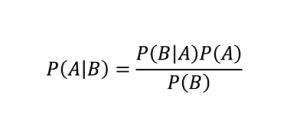

P (A | B)：假設事件 B 已經發生，事件 A 發生的條件概率。 （也稱為後驗概率）

P(A)：事件 A 的概率。

P(B)：事件 B 的概率。

P (B | A)：假設事件 A 已經發生，事件 B 發生的條件概率。

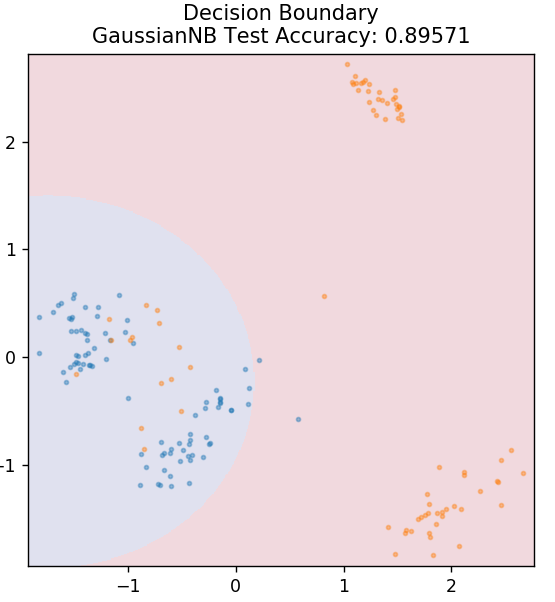
你問為什麼這個算法被命名為 Naive？ 這是因為它假設所有事件的發生都是相互獨立的。 所以每個特徵分別定義了一個數據點所屬的類，它們之間沒有任何依賴關係。 樸素貝葉斯是文本分類的最佳選擇。 即使是少量的訓練數據，它也能很好地工作。

從 sklearn.naive_bayes 導入 GaussianNB

模型 = GaussianNB()

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

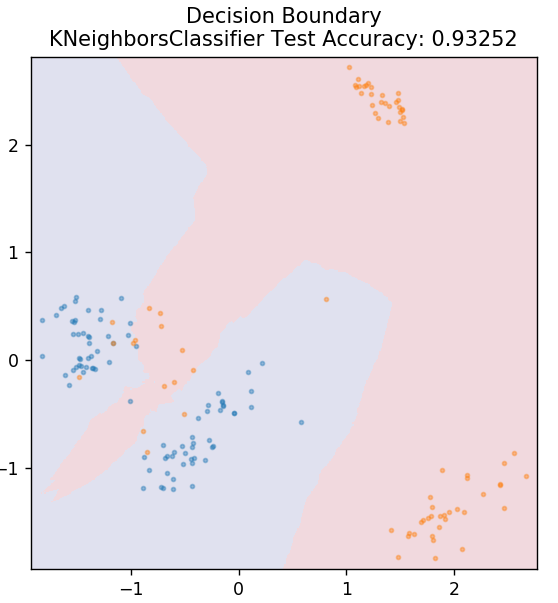
5.KNN

KNN 代表 K-最近鄰。 它是一種使用非常廣泛的監督學習算法，它根據測試數據與之前分類的訓練數據的相似性對測試數據進行分類。 KNN 在訓練期間不會對所有數據點進行分類。 相反，它只存儲數據集，當它獲得任何新數據時，它會根據它們的相似性對這些數據點進行分類。 它通過計算該數據點的 K 個最近鄰居（此處為n_neighbors ）的歐幾里德距離來實現。

從 sklearn.neighbors 導入 KNeighborsClassifier

模型 = KNeighborsClassifier（n_neighbors = 20）

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

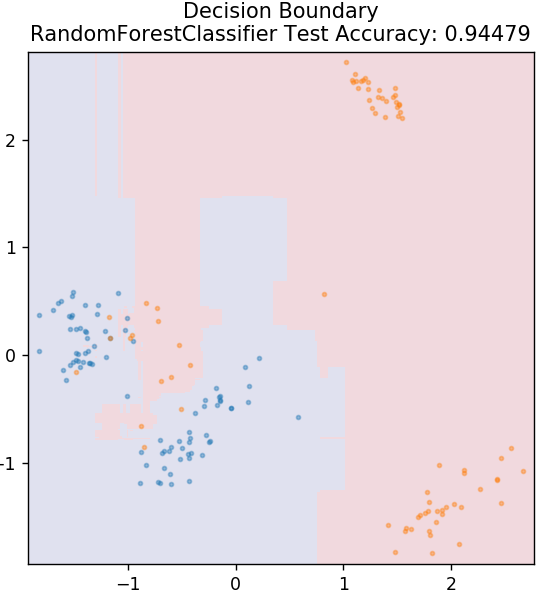
6. 隨機森林

隨機森林是一種非常簡單且多樣化的機器學習算法，它使用監督學習技術。 正如您可以從名稱中猜到的那樣，隨機森林由大量決策樹組成，充當一個整體。 每個決策樹都會計算出數據點的輸出類別，並選擇多數類別作為模型的最終輸出。 這裡的想法是，處理相同數據的更多樹往往比單個樹的結果更準確。

從 sklearn.ensemble 導入 RandomForestClassifier

模型 = RandomForestClassifier()

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

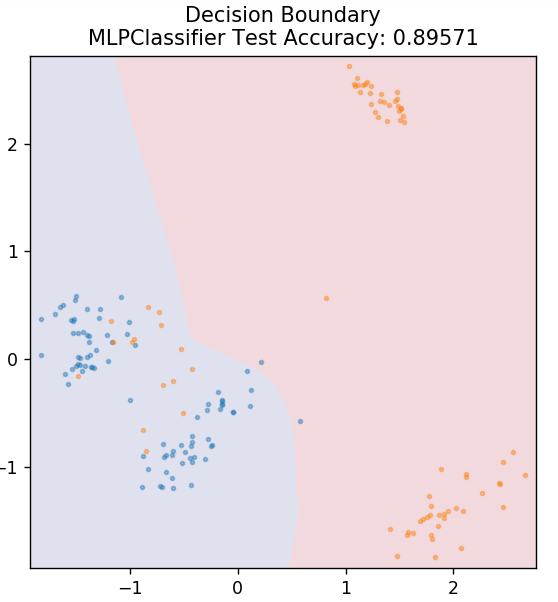
7. 多層感知器

多層感知器（或 MLP）是一種非常迷人的算法，屬於深度學習的分支。 更具體地說，它屬於前饋人工神經網絡 (ANN) 類。 MLP 形成一個由至少三層的多個感知器組成的網絡：輸入層、輸出層和隱藏層。 MLP 能夠區分非線性可分的數據。

隱藏層中的每個神經元都使用激活函數進入下一層。 在這裡，反向傳播算法用於實際調整參數，從而訓練神經網絡。 它主要用於簡單的回歸問題。

從 sklearn.neural_network 導入 MLPClassifier

模型 = MLPClassifier()

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

另請閱讀： Python 項目理念和主題

結論

我們可以得出結論，不同的機器學習算法會產生不同的決策邊界，因此不同的準確性會導致對同一數據集進行分類。

一般來說，沒有辦法將任何算法聲明為所有類型數據的最佳算法。 機器學習需要對各種算法進行嚴格的試驗和錯誤，以確定分別對每個數據集最有效的方法。 ML 算法的列表顯然不會到此結束。 在 Python 的 Scikit-Learn 庫中還有大量其他技術等待探索。 繼續使用所有這些訓練您的數據集，玩得開心！

如果您有興趣了解有關決策樹、機器學習的更多信息，請查看 IIIT-B 和 upGrad 的機器學習和人工智能執行 PG 計劃，該計劃專為工作專業人士設計，提供 450 多個小時的嚴格培訓、30 多個案例研究和任務、IIIT-B 校友身份、5 個以上實用的實踐頂點項目和頂級公司的工作協助。