概率密度函數簡介【公式、性質、應用、實例】

概率密度函數 (PDF) 是統計中的表達式，表示離散隨機變量的概率分佈。 簡單來說，概率分佈可以定義為隨機變量（如股票或 ETF）的結果的可能性。 離散變量與可以確定準確值的連續隨機變量相反。

例如，股票市場中的股票價值在離散隨機變量中只有兩個小數點（例如，65.76），而不是具有任意小數點的連續變量（例如：65.7685434567）。

概率密度函數是一種統計工具，用於確定離散隨機變量結果的可能性。 在圖表上繪製時，PDF 看起來與鍾形曲線相同，其中曲線下的面積代表結果的概率。

當投影為圖形模型時，曲線下的面積表示離散隨機變量的值將落入的範圍。 因此，曲線下的總面積等於變量結果的概率。

概率密度函數可以確定隨機變量落在特定值範圍內的可能性。

通常，概率密度函數分析與股票市場中特定基金相關的風險和潛在收入。

被視為概率密度函數的函數要滿足的條件

與可以具有無限個值的連續變量相比，可以準確測量離散變量的值。 任何函數都應滿足以下兩個條件才能成為概率密度函數：

• 隨機變量的每個可能值的 f(x) 值應為正（非負）。
• 曲線總面積的積分值（隨機變量所有可能值的積分）應為 1。

概率密度函數和概率分佈函數的區別

隨機變量可以有很多值。 對隨機變量可能具有的每個可能值的描述稱為其概率分佈。

概率分佈給出了一組結果及其相關概率。 表示連續概率分佈的統計函數稱為概率密度函數。

還有另一種表示離散概率分佈的統計工具，稱為概率質量函數。 這詳細說明了所有可能的結果及其可能性概率。

概率密度函數的表達式

如果隨機變量是離散的，則其概率分佈稱為概率質量函數，如果是連續變量，則其概率分佈稱為概率密度函數。

當所討論的隨機變量具有一系列可能值時，使用 PDF。 它們的概率分佈用於確定準確值。

讓隨機變量用X表示。隨機變量X的概率密度函數f可以表示為

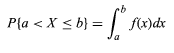
• 隨機變量的值介於 a 和 b 之間。
• 如果 X 表示從範圍（區間）r 和 s 中選擇特定數的概率，則概率密度函數可以表示為

f ( x ) = 1/( s − r ) 對於r < x < s和f ( x ) = 0 對於x < r或x > s 。

• PDF F 表示為：

F ( x ) = P { X ≤ x }

稱為 X 的分佈函數或累積分佈函數。

考慮到隨機變量 X 有一個概率分佈函數f ( x )，那麼 f 和 F 之間的關係可以建立為

F ′(. x ) = f ( x )

離散隨機變量的分佈函數不同於其概率分佈函數。 兩者的關係可以表示如下：

隨機變量的期望表示為，

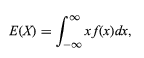
因此，在組合理論的幫助下，可以統一處理所有離散和隨機變量。

概率密度函數公式

連續隨機變量 X 在某個固定值 x 上的概率始終為 0。在這種情況下，不能使用 P(X = x)。 應確定位於值範圍 (a,b) 之間的 X 值。 為了確定相同，使用以下公式。

概率密度函數的性質

例如，取值在 (a,b) 範圍內的連續隨機變量將通過計算曲線下面積和以 (a) 作為其下限和 (b) 作為其繪製的 X 軸的面積來估計上限。 上述的概率密度函數表示為：

對於所有可能的值，概率密度函數都是正的（非負的）。 這意味著對於每個 x，f(x)≥ 0。 密度曲線和 X 軸（水平軸）之間的面積等於 1。

這也可以表示為：

密度函數曲線在給定範圍內是連續的，它是針對一系列連續值或變量域明確定義的。

加入來自世界頂級大學的在線機器學習課程——碩士、高級管理人員研究生課程和 ML 和 AI 高級證書課程，以加快您的職業生涯。

概率密度函數的應用

• 概率密度函數用於大氣 NO 濃度水平的年度建模。
• 柴油發動機燃燒建模。
• 在統計學中，概率密度函數用於確定隨機變量結果的可能性。

概率密度函數示例

• 示例 1

以下是如何使用概率密度函數 (PDF) 來確定投資者在股票市場中的潛在風險的示例：

首先，PDF 是根據歷史信息生成的圖形工具。

PDF 最常見的形式是中性投影，其中風險等於各種可能性的回報。 風險承擔能力較低的投資者只會獲得有限的利潤，因此他們處於鍾形曲線的左側。 相反，具有高風險承擔能力的投資者可能會獲得更高的收益率，因此落在曲線的右側。

大多數投資者處於平均風險承擔能力之下，因此他們佔據了曲線的中間。

這有助於根據收到的數據分析投資者的類別。 這有助於股票市場經紀人確定他們的目標客戶類別以銷售他們的產品。

• 示例 2

概率密度函數的基本應用之一是高斯隨機變量，也稱為正態隨機變量。

在這兩種情況下，該圖都給出了概率密度函數的鐘形曲線。

密度可以表示為

上述密度方程的圖表如下所示。

曲線下的面積代表高斯隨機變量的實際值。

結論

概率密度函數在機器學習中起著至關重要的作用。 對於著眼於機器學習和人工智能職業的學生，我們強烈建議註冊 upGrad 的機器學習 IIT 高級證書課程。 該計劃是定制的，旨在使高級工作專業人員能夠使用雲計算技術部署機器學習模型。

該課程由 IIT Madras 的教師和行業專家設計，以使學習過程更加相關和實用。 該計劃提供來自印度令人垂涎的排名第一的工程學院的全球認可認證以及 upGrad 的 360 度就業支持。

更重要的是，您有大量機會與 upGrad 的 40,000 多名付費學習者合作開展大型項目。

前往我們的網站開始您的學習之旅！