機器學習中的多元回歸簡介：完整指南

今天的技術是數據驅動的，這已經不是什麼秘密了。 數據可能只是數字的彙編，但可以對其進行有意義的處理，以提取生產力和資源，使企業長期保持競爭力和可持續發展。 碰巧的是，數據分析是從原始信息中得出準確估計的答案。

數據分析是一種涉及統計和邏輯思想的技術，用於審查、處理數據並將其轉換為可用形式。 數據分析得出的解決方案用於企業做出重要決策。 數據科學與數據分析一起用於高精度預測未來結果。 這是一個使用科學技術和算法從數據池中獲取可行信息的過程。

數據專業人員面臨的一個常見問題是如何確定響應變量（用 Y 表示）和解釋變量（用 Xi 表示）之間是否存在統計關係。

這個問題的答案是回歸分析。 讓我們更詳細地了解這一點。

什麼是回歸分析？

回歸分析是遵循受控或監督機器學習算法的數據分析中的流行方法之一。 它是一種識別和建立數據變量之間關係的有效技術。

回歸分析涉及使用數學策略對可行變量進行分類，以對這些分類變量得出高度準確的結論。

什麼是多元回歸？

多變量是一種分析多個數據變量的受控或監督機器學習算法。 它是多元回歸的延續，涉及一個因變量和許多自變量。 根據自變量的數量預測輸出。

多元回歸計算出一個公式，該公式解釋了變量中存在的因素對其他因素變化的同時響應。 它們用於研究各個領域的數據。 例如，在房地產中，多元回歸用於根據位置、房間數量和可用設施等幾個因素來預測房屋的價格。

多元回歸中的成本函數

當模型的結果偏離觀察到的數據時，成本函數會為樣本分配成本。 成本函數方程是預測值與實際值之差的平方除以數據集長度的兩倍。

這是一個例子：

結果：

資源

如何使用多元回歸分析？

多元回歸分析涉及的過程包括特徵選擇、特徵工程、特徵歸一化、選擇損失函數、假設分析和創建回歸模型。

1. 特徵的選擇：這是多元回歸中最重要的一步。 也稱為變量選擇，此過程涉及選擇可行的變量以建立有效的模型。
2. 特徵歸一化：這涉及特徵縮放以保持流線型分佈和數據比率。 這有助於更好的數據分析。 可以根據需要更改所有特徵的值。
3. 選擇損失函數和假設：損失函數用於預測錯誤。 當假設預測與實際數字發生變化時，損失函數就會發揮作用。 在這裡，假設表示從特徵或變量預測的值。
4. 固定假設參數：假設的參數是固定的或設置為使其最小化損失函數並增強更好的預測。
5. 減少損失函數：通過生成專門用於數據集損失最小化的算法來最小化損失函數，這反過來又有助於改變假設參數。 梯度下降是最常用的損失最小化算法。 一旦損失最小化完成，該算法也可以用於其他操作。
6. 分析假設函數：需要分析假設的函數，因為它對於預測值至關重要。 在分析函數之後，然後在測試數據上對其進行測試。

現在讓我們看看可以使用多元回歸的兩種方式。

1. 多元線性回歸

多元線性回歸類似於簡單線性回歸，只是在多元線性回歸中，多個自變量對因變量有貢獻，因此在計算中使用了多個係數。

• 它用於推導多個隨機變量之間的數學關係。 它解釋了有多少多個自變量與一個因變量相關聯。
• 多個自變量的詳細信息用於準確預測它們對結果變量的影響。
• 多元線性回歸模型以線性形式（直線形式）生成每個數據點的最佳近似關係。
• 多元線性回歸模型的方程為：

yi​=β0​+β1​xi1​+β2​xi2​+…+βp​xip​+

對於 i=n 觀察，其中：

資源

什麼時候可以使用線性回歸？

線性回歸模型只有在有兩個連續變量且一個依賴另一個獨立的情況下才可以使用。

自變量用作確定因變量的值或結果的參數。

2. 多元邏輯回歸

邏輯回歸是一種用於基於多個自變量預測二元結果的算法。 二元結果有兩種可能性，或者場景發生（用 1 表示）或者它沒有發生（用 0 表示）。

在處理二元數據時使用邏輯回歸，即結果（或因變量）是二分法的數據。

邏輯回歸可以用在什麼地方？

邏輯回歸主要用於處理分類問題。 例如，確定電子郵件是否為垃圾郵件以及特定交易是否是惡意的。 在數據分析中，它用於做出有計劃的決策，以最大限度地減少損失並增加利潤。

當存在一個因變量和多個結果時，使用多變量邏輯回歸。 它與邏輯回歸的不同之處在於有兩個以上的可能結果。

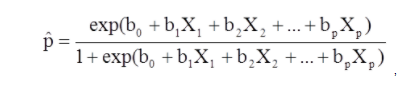
X1 到 Xp 是不同的自變量。

b0 到 bp 是回歸係數

多元邏輯回歸模型也可以寫成不同的形式。 在下面的表格中，結果是結果出現概率的預期對數，

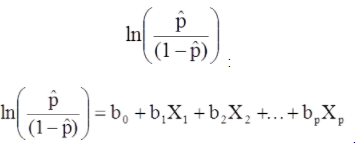
多元邏輯回歸模型也可以寫成不同的形式。 在下面的表格中，結果是結果出現概率的預期對數。

上式右邊類似於線性回歸方程，但求出回歸係數的方法不同。

多元回歸模型中的假設

• 因變量和自變量具有線性關係。
• 自變量之間沒有很強的相關性。
• yi 的觀察值是從總體中隨機且單獨地選擇的。

多元邏輯回歸模型中的假設

• 因變量是名義變量或有序變量。 名義變量有兩個或多個類別，沒有任何有意義的組織。 序數變量也可以有兩個或多個類別，但它們具有結構並且可以排序。
• 可以有單個或多個自變量，可以是有序的、連續的或名義的。 連續變量是在特定範圍內可以具有無限值的變量。
• 因變量是互斥且窮舉的。
• 自變量之間沒有很強的相關性。

多元回歸的優點

1. 多元回歸幫助我們研究數據集中多個變量之間的關係。
2. 因變量和自變量之間的相關性有助於預測結果。
3. 它是機器學習中最方便、最流行的算法之一。

多元回歸的缺點

• 多元技術的複雜性需要復雜的數學計算。
• 解釋多元回歸模型的輸出並不容易，因為損失和錯誤輸出存在不一致。
• 多元回歸模型不能應用於較小的數據集； 它們旨在在涉及更大的數據集時產生準確的輸出。

如果您想了解有關多元回歸和其他復雜數據科學主題的更多信息，upGrad 正是您的解決方案。 我們來自利物浦約翰摩爾斯大學的為期 18 個月的數據科學理學碩士課程涵蓋 500 多個嚴格的學習時間、25 節輔導課程（以 1:8 的方式舉行）和 20 多個現場課程。 upGrad 還提供 1:1 教學協助和 360° 職業指導支持，幫助學生轉變職業生涯。 學習者可以在全球平台上與超過 40,000 名付費學習者一起利用對等學習，並在六個職能專業領域開展合作項目，以最大限度地提高他們的學習體驗。