機器學習中的梯度下降：它是如何工作的？

介紹

機器學習最關鍵的部分之一是優化其算法。 機器學習中幾乎所有的算法都有一個優化算法作為算法的核心。 眾所周知，優化是任何算法的最終目標，即使是處理現實生活中的事件或處理市場上基於技術的產品時也是如此。

目前有很多優化算法用於人臉識別、自動駕駛汽車、基於市場的分析等多種應用中。同樣，在機器學習中，此類優化算法也發揮著重要作用。 一種如此廣泛使用的優化算法是我們將在本文中介紹的梯度下降算法。

什麼是梯度下降？

在機器學習中，梯度下降算法是最常用的算法之一，但它卻讓大多數新手感到困惑。 在數學上，梯度下降是一種一階迭代優化算法，用於找到可微函數的局部最小值。 簡單來說，這種梯度下降算法用於找到函數參數（或係數）的值，這些參數用於盡可能低地最小化成本函數。 成本函數用於量化構建的機器學習模型的預測值與實際值之間的誤差。

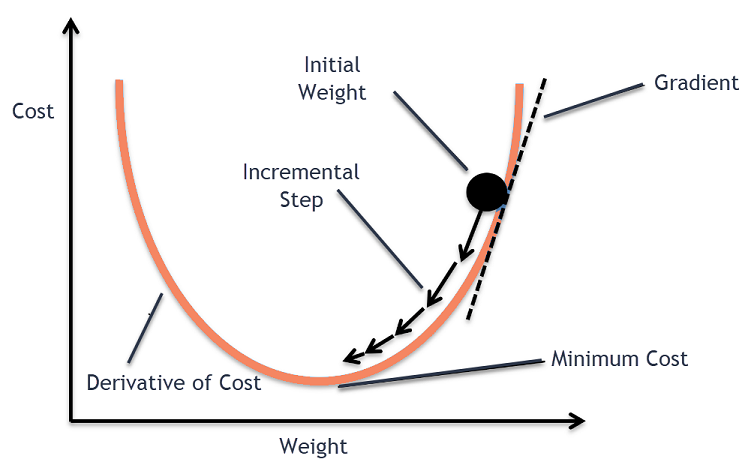
梯度下降直覺

考慮一個大碗，你通常會用它來盛水果或吃麥片。 這個碗將是成本函數（f）。

現在，碗表面任何部分的隨機坐標將是成本函數係數的當前值。 碗的底部是最好的係數集，它是函數的最小值。

在這裡，目標是每次迭代計算係數的不同值，評估成本並選擇具有更好成本函數值（較低值）的係數。 在多次迭代中，會發現碗的底部具有最小化成本函數的最佳係數。

以這種方式，梯度下降算法起作用以產生最小的成本。

加入來自世界頂級大學的在線機器學習課程——碩士、高管研究生課程和 ML 和 AI 高級證書課程，以加快您的職業生涯。

梯度下降程序

這個梯度下降過程從最初為成本函數的係數分配值開始。 這可以是接近 0 的值或小的隨機值。

係數 = 0.0

接下來，通過將其應用於成本函數併計算成本來獲得係數的成本。

成本 = f（係數）

然後，計算成本函數的導數。 成本函數的這種導數是通過微積分的數學概念獲得的。 它為我們提供了函數在計算其導數的給定點的斜率。 這個斜率需要知道在下一次迭代中係數將向哪個方向移動以獲得較低的成本值。 這是通過觀察計算的導數的符號來完成的。

delta = 導數（成本）

一旦我們從計算的導數中知道哪個方向是下坡，我們需要更新係數值。 為此，一個參數稱為學習參數，使用 alpha (α)。 這用於控制係數在每次更新時可以改變的程度。

係數 = 係數 - (alpha * delta)

資源

以這種方式，重複此過程，直到係數的成本等於 0.0 或足夠接近於零。 這是梯度下降算法的過程。

梯度下降算法的類型

在現代，現代機器學習和深度學習算法中使用了三種基本類型的梯度下降。 這三種類型之間的主要區別在於其計算成本和效率。 根據使用的數據量、時間複雜度和準確性，以下是三種類型。

1. 批量梯度下降
2. 隨機梯度下降
3. 小批量梯度下降

批量梯度下降

這是梯度下降算法的第一個也是基本版本，其中一次使用整個數據集來計算成本函數及其梯度。 由於整個數據集一次性更新，因此這種類型的梯度計算可能非常緩慢，並且對於那些超出設備內存容量的數據集是不可能的。

因此，這種批量梯度下降算法僅用於較小的數據集，並且當訓練示例的數量很大時，批量梯度下降不是首選。 相反，使用隨機和小批量梯度下降算法。

隨機梯度下降

這是另一種梯度下降算法，其中每次迭代只處理一個訓練示例。 在此，第一步是隨機化整個訓練數據集。 然後，僅使用一個訓練樣本來更新係數。 這與批量梯度下降形成對比，其中僅在評估所有訓練示例時才更新參數（係數）。

隨機梯度下降 (SGD) 的優點是這種類型的頻繁更新提供了詳細的改進率。 然而，在某些情況下，這可能會在計算上變得昂貴，因為它每次迭代只處理一個示例，這可能導致迭代次數非常大。

小批量梯度下降

這是一種最近開發的算法，比批處理和隨機梯度下降算法都快。 它是最優選的，因為它是前面提到的兩種算法的組合。 在這種情況下，它將訓練集分成幾個小批次，並在計算該批次的梯度後對每個批次執行更新（如在 SGD 中）。

通常，批量大小在 30 到 500 之間變化，但沒有任何固定大小，因為它們因不同的應用程序而異。 因此，即使有一個巨大的訓練數據集，這個算法也會在“b”個小批量中處理它。 因此，它適用於迭代次數較少的大型數據集。

如果 'm' 是訓練示例的數量，那麼如果 b==m，Mini Batch Gradient Descent 將類似於 Batch Gradient Descent 算法。

機器學習中梯度下降的變體

有了梯度下降的這個基礎，已經開發了其他幾種算法。 其中一些總結如下。

香草梯度下降

這是梯度下降技術的最簡單形式之一。 香草這個名字意味著純淨或沒有任何摻假。 在這種情況下，通過計算成本函數的梯度，朝著最小值的方向邁出一小步。 與上述算法類似，更新規則由下式給出，

係數 = 係數 - (alpha * delta)

動量梯度下降

在這種情況下，算法使得我們在採取下一步之前知道前面的步驟。 這是通過引入一個新術語來完成的，該術語是先前更新的乘積和稱為動量的常數。 在此，權重更新規則由下式給出，

更新 = 阿爾法 * 德爾塔

速度 = previous_update * 動量

係數 = 係數 + 速度 - 更新

阿達格拉德

ADAGRAD 一詞代表自適應梯度算法。 顧名思義，它使用自適應技術來更新權重。 該算法更適合稀疏數據。 這種優化會根據訓練期間參數更新的頻率改變其學習率。 例如，具有較高梯度的參數具有較慢的學習率，因此我們最終不會超過最小值。 同樣，較低的梯度具有更快的學習率，可以更快地得到訓練。

亞當

另一種源於梯度下降算法的自適應優化算法是 ADAM，它代表自適應矩估計。 它是 ADAGRAD 和 SGD 與 Momentum 算法的組合。 它是從 ADAGRAD 算法構建的，並且有進一步的缺點。 簡單來說，ADAM = ADAGRAD + Momentum。

這樣一來，世界上已經開發和正在開發的梯度下降算法的其他幾種變體，例如AMSGrad、ADAMax。

結論

在本文中，我們看到了機器學習中最常用的優化算法之一背後的算法，即梯度下降算法及其已開發的類型和變體。

upGrad 提供機器學習和人工智能的執行 PG 計劃和機器學習和人工智能的理學碩士，可以指導您建立職業生涯。 這些課程將解釋機器學習的必要性以及收集該領域知識的進一步步驟，涵蓋從機器學習中的梯度下降等各種概念。