高斯樸素貝葉斯:你需要知道什麼?
已發表: 2021-02-22目錄
高斯樸素貝葉斯
樸素貝葉斯是一種用於許多分類功能的概率機器學習算法,它基於貝葉斯定理。 高斯樸素貝葉斯是樸素貝葉斯的擴展。 雖然其他函數用於估計數據分佈,但高斯或正態分佈是最容易實現的,因為您需要計算訓練數據的均值和標準差。
什麼是樸素貝葉斯算法?
樸素貝葉斯是一種概率機器學習算法,可用於多種分類任務。 樸素貝葉斯的典型應用是文檔分類、過濾垃圾郵件、預測等。 該算法基於 Thomas Bayes 的發現,因此得名。
之所以使用“Naive”這個名稱,是因為該算法在其模型中包含了彼此獨立的特徵。 對一個特徵值的任何修改都不會直接影響算法的任何其他特徵的值。 樸素貝葉斯算法的主要優點是它是一種簡單而強大的算法。
它基於概率模型,可以輕鬆地對算法進行編碼,並且可以實時快速進行預測。 因此,該算法是解決實際問題的典型選擇,因為它可以調整為立即響應用戶請求。 但在我們深入研究樸素貝葉斯和高斯樸素貝葉斯之前,我們必須知道條件概率是什麼意思。
條件概率解釋
我們可以通過一個例子更好地理解條件概率。 當你拋硬幣時,領先或落後的概率為 50%。 同樣,當你擲骰子時,得到 4 的概率是 1/6 或 0.16。
如果我們拿一副牌,假設它是黑桃,得到一張 Q 的概率是多少? 由於已經設置了必須是黑桃的條件,因此分母或選擇集變為 13。黑桃中只有一個皇后,因此選擇黑桃皇后的概率變為 1/13= 0.07。

事件 A 給定事件 B 的條件概率是指在事件 B 已經發生的情況下,事件 A 發生的概率。 在數學上,給定 B 的 A 的條件概率可以表示為 P[A|B] = P[A AND B] / P[B]。
讓我們考慮一個稍微複雜的例子。 以一所共有 100 名學生的學校為例。 這個人群可以分為 4 類——學生、教師、男性和女性。 考慮下面給出的表格:
| 女性 | 男性 | 全部的 | |
| 老師 | 8 | 12 | 20 |
| 學生 | 32 | 48 | 80 |
| 全部的 | 40 | 50 | 100 |
在這裡,在給定他是男人的條件下,學校的某個居民是老師的條件概率是多少。
要計算這一點,您必須過濾 60 名男性的子群體並向下鑽取到 12 名男教師。
所以,期望的條件概率 P[Teacher | 男] = 12/60 = 0.2
P(教師|男)= P(教師∩男)/P(男)= 12/60 = 0.2
這可以表示為教師(A)和男性(B)除以男性(B)。 同理,B給定A的條件概率也可以計算出來。 我們用於樸素貝葉斯的規則可以從以下符號中得出:
P (A | B) = P (A ∩ B) / P(B)
P (B | A) = P (A ∩ B) / P(A)
貝葉斯法則
在貝葉斯規則中,我們從可以從訓練數據集中找到的 P (X | Y) 找到 P (Y | X)。 為此,您只需將上述公式中的 A 和 B 替換為 X 和 Y。 對於觀察,X 是已知變量,Y 是未知變量。 對於數據集的每一行,假設 X 已經發生,您必須計算 Y 的概率。

但是,如果 Y 中的類別超過 2 個,會發生什麼情況? 我們必須計算每個 Y 類的概率以找出獲勝的類。
通過貝葉斯規則,我們從 P (X | Y) 找到 P (Y | X)
從訓練數據中得知:P(X | Y) = P(X ∩ Y) / P(Y)
P(證據|結果)
未知 – 對測試數據進行預測:P (Y | X) = P (X ∩ Y) / P(X)
P(結果|證據)
貝葉斯法則 = P (Y | X) = P (X | Y) * P (Y) / P (X)
樸素貝葉斯
貝葉斯規則提供了給定條件 X 的 Y 概率公式。但在現實世界中,可能存在多個 X 變量。 當你有獨立的特徵時,貝葉斯規則可以擴展到樸素貝葉斯規則。 X 是相互獨立的。 樸素貝葉斯公式比貝葉斯公式更強大
高斯樸素貝葉斯
到目前為止,我們已經看到 X 屬於類別,但是當 X 是連續變量時如何計算概率? 如果我們假設 X 遵循特定分佈,則可以使用該分佈的概率密度函數來計算似然概率。
如果我們假設 X 服從高斯或正態分佈,我們必須代入正態分佈的概率密度並將其命名為高斯樸素貝葉斯。 要計算此公式,您需要 X 的均值和方差。
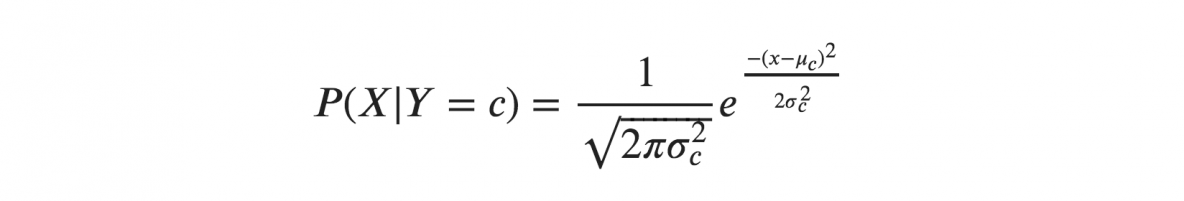
在上述公式中,sigma 和 mu 是為給定的 Y 類 c 計算的連續變量 X 的方差和均值。
高斯樸素貝葉斯的表示
上面的公式通過頻率計算了每個類的輸入值的概率。 我們可以計算整個分佈中每個類別的 x 的均值和標準差。
這意味著除了每個類的概率,我們還必須存儲該類的每個輸入變量的均值和標準差。
平均值(x)= 1/n * 總和(x)
其中 n 表示實例數,x 是數據中輸入變量的值。
標準差(x) = sqrt(1/n * sum(xi-mean(x)^2 ))
這裡計算每個 x 的平均值和 x 的平均值的平方根,其中 n 是實例數,sum() 是求和函數,sqrt() 是平方根函數,xi 是特定的 x 值.

使用高斯樸素貝葉斯模型進行預測
高斯概率密度函數可用於通過用變量的新輸入值替換參數來進行預測,因此,高斯函數將給出新輸入值概率的估計值。
樸素貝葉斯分類器
樸素貝葉斯分類器假設一個特徵的值獨立於任何其他特徵的值。 樸素貝葉斯分類器需要訓練數據來估計分類所需的參數。 由於設計和應用簡單,樸素貝葉斯分類器可以適用於許多現實生活場景。
結論
高斯樸素貝葉斯分類器是一種快速簡單的分類器技術,無需太多努力就能很好地工作,而且準確度很高。
如果您有興趣了解更多關於人工智能、機器學習的信息,請查看 IIIT-B 和 upGrad 的機器學習和人工智能 PG 文憑,該文憑專為在職專業人士設計,提供 450 多個小時的嚴格培訓、30 多個案例研究和作業, IIIT-B 校友身份、5 個以上實用的實踐頂點項目和頂級公司的工作協助。
從世界頂級大學學習ML 課程。 獲得碩士、Executive PGP 或高級證書課程以加快您的職業生涯。
什麼是樸素貝葉斯算法?
樸素貝葉斯是一種經典的機器學習算法。 樸素貝葉斯起源於統計學,是一種簡單而強大的算法。 樸素貝葉斯是基於應用條件概率分析的分類器家族。 在該分析中,使用構成事件的每個單獨事件的概率來計算事件的條件概率。 樸素貝葉斯分類器在實踐中經常被發現非常有效,尤其是當特徵集的維數很大時。
樸素貝葉斯算法有哪些應用?
樸素貝葉斯用於文本分類、文檔分類和文檔索引。 在樸素貝葉斯中,每個可能的特徵在預處理階段沒有分配任何權重,而權重隨後在訓練和識別階段分配。 樸素貝葉斯算法的基本假設是特徵是獨立的。
什麼是高斯樸素貝葉斯算法?
高斯樸素貝葉斯是一種基於應用貝葉斯定理和強獨立假設的概率分類算法。 在分類的上下文中,獨立性是指特徵的一個值的存在不會影響另一個值的存在(與概率論中的獨立性不同)。 樸素是指使用對象的特徵相互獨立的假設。 在機器學習的背景下,樸素貝葉斯分類器以具有高度表達性、可擴展性和相當準確的特點而著稱,但它們的性能隨著訓練集的增長而迅速惡化。 許多特徵有助於樸素貝葉斯分類器的成功。 最值得注意的是,它們不需要對分類模型的參數進行任何調整,它們可以很好地適應訓練數據集的大小,並且可以輕鬆處理連續特徵。
