機器學習中的鍊式法則導數：解釋

機器學習已經發展成為近年來最受關注和研究的領域之一，並且有充分的理由。 機器學習的新模型和應用每天都在被發現，全球的研究人員都在為下一件大事而努力。

因此，來自不同背景的專業人士越來越有興趣轉向機器學習並成為這場正在進行的革命的一部分。 如果您是這樣的機器學習愛好者，希望邁出第一步，那麼讓我們告訴您，首先要了解數學和統計學的基礎知識。

與機器學習高度相關的數學中一個重要的主題是導數。 根據您對微積分的基本了解，您會記得任何函數的導數都是該函數的瞬時變化率。 在這篇博客中，我們將深入研究衍生品並探索鍊式法則。 當我們改變方程中的一些自變量時，我們將看到特定函數的輸出如何變化。 借助鍊式規則導數的知識，您將能夠區分在機器學習中肯定會遇到的更複雜的函數。

從世界頂級大學在線獲得機器學習認證——碩士、高管研究生課程和 ML 和 AI 高級證書課程，以加快您的職業生涯。

了解鍊式法則導數

鍊式法則本質上是一個數學公式，可以幫助您計算複合函數的導數。 複合函數是由兩個或多個函數組成的函數。 所以，如果f和g是兩個函數，那麼鍊式法則將幫助我們找到復合函數的導數，例如fog或go f。

考慮到復合函數霧，鍊式法則導數如下所示：

上面的規則也可以寫成：

其中函數F是f 和 g的組合，形式為 f(g(x))。

現在，假設我們有三個變量，其中第三個變量 (z) 取決於第二個變量 (y)，而第二個變量又取決於第一個變量 (x)。 在這種情況下，鍊式規則導數看起來像這樣：

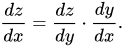在深度學習方面，這也是經常用來解決反向傳播問題的公式。 現在，由於我們提到 z 依賴於 y 和 y 依賴於 x，我們可以寫成 z = f(y) 和 y = g(x)。 這種替換將以以下方式修改我們的微分方程：

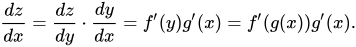現在，讓我們看一些鍊式法則導數的例子，以更好地理解它們背後的數學原理。

鍊式規則導數的例子和應用

讓我們從維基百科中舉一個著名的例子來更好地理解鍊式規則導數。 假設你從天上自由落體。 您在秋季遇到的大氣壓力會不斷變化。 這是一個繪製大氣壓力隨海拔高度變化的圖表：

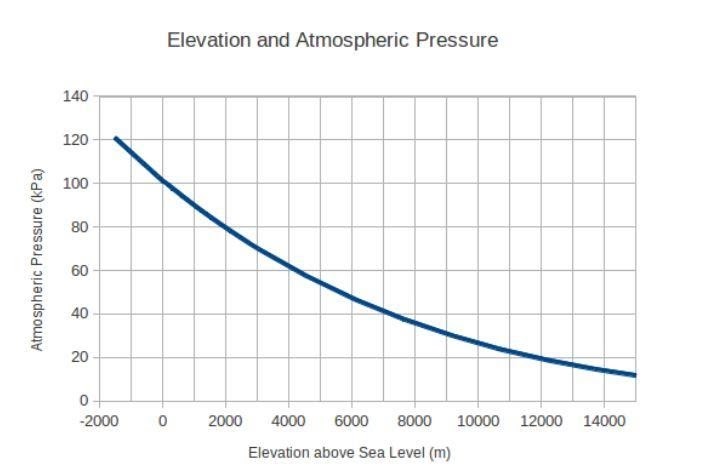
假設你的墜落始於海拔 4000 米。 最初，您的速度為零，由於重力，加速度值為每秒 9.8 米。

現在，讓我們將這種情況與之前的鍊式法則方法進行比較。 在本例中，我們將使用變量“t”來表示時間而不是 x。

然後，變量 y = g(t) 表示自秋季開始以來行進的距離，可以如下給出：

g(t) = 0.5*9.8t^2

並且，海平面的高度可以由變量“h”給出，它等於 400-g(t)。

假設，基於一個模型，我們還可以將任意高度h處的大氣壓函數寫為：

f(h) = 101325 e−0.0001h

現在，您可以根據它們的因變量區分這兩個方程，以獲得以下結果：

g′(t) = -9.8t,

在這裡，g'(t) 告訴您在任何時間t的速度值。

f′(h) = -10.1325e-0.0001h

這裡，f'(h) 是大氣壓相對於高度 h 的變化率。 現在，問題是我們能否將這兩個方程結合起來，得出大氣壓隨時間的變化率？ 讓我們看看使用鍊式法則：

我們得到的最後一個方程為我們提供了大氣壓力相對於自秋天以來經過的時間的變化率。 在機器學習方面，神經網絡不斷需要關於神經元預測誤差的權重更新。 鍊式法則有助於調整這些權重並使機器學習模型更接近正確的輸出。

結論

如您所見，鍊式法則有很多用途。 尤其是在機器學習或深度學習方面，鍊式法則在更新神經元的權重和提高模型的整體效率方面有很大的用處。

現在您已經了解了鍊式法則的基礎知識，請繼續嘗試自己解決一些問題。 查找一些複合函數並嘗試找到它們的導數。 你練習得越多，你的概念就會越清晰，你就越容易訓練你的機器學習模型！ 也就是說，如果您是機器學習愛好者，但在努力邁出該領域的第一步，那麼 upGrad 將為您提供支持！

我們的機器學習和人工智能執行 PG 計劃與 IIIT-Bangalore 合作提供，為您提供六種行業相關專業的選擇。 該課程從底層開始，將您帶到頂點，同時為您提供來自行業專家的一對一支持、強大的同齡學生群體以及 360 度的職業支持。