二叉樹與二叉搜索樹:二叉樹和二叉搜索樹之間的區別
已發表: 2021-01-21目錄
介紹
排序是按系統順序排列數據以便更有效地分析數據的過程。 識別特定記錄的過程稱為搜索。 如果數據按特定順序正確排序,則搜索將成為一項簡單而有效的任務。 本文處理最重要的非線性數據結構之一,即樹。
樹主要用於通過展示元素之間的層次關係來表示數據。 例如,目錄、家譜。 從技術上講,一棵樹可以定義為一個或多個節點的有限集“T”,使得一個節點被指定為樹的根,而其他節點被劃分為 n>=0 不相交集 T1、T2、T3, T4…… Tn 和被稱為該根節點的子樹或子節點。
什麼是二叉樹?
二叉樹是一種非線性數據結構,其中一個節點可以有 0、1 或 2 個節點。 二叉樹中的每個節點都稱為父節點或子節點。 二叉樹的最高節點稱為根節點。 每個父節點最多可以有 2 個子節點,即左子節點和右子節點。
二叉樹中的節點具有三個字段:
- 數據元素——它存儲節點要存儲的數據值。
- 指向左子節點的指針——它存儲對左子節點的引用(或地址)。
- 指向右子節點的指針——它存儲對右子節點的引用。
這樣,幾個節點組合在一起就構成了一個二叉樹。
二叉樹可以表示為:
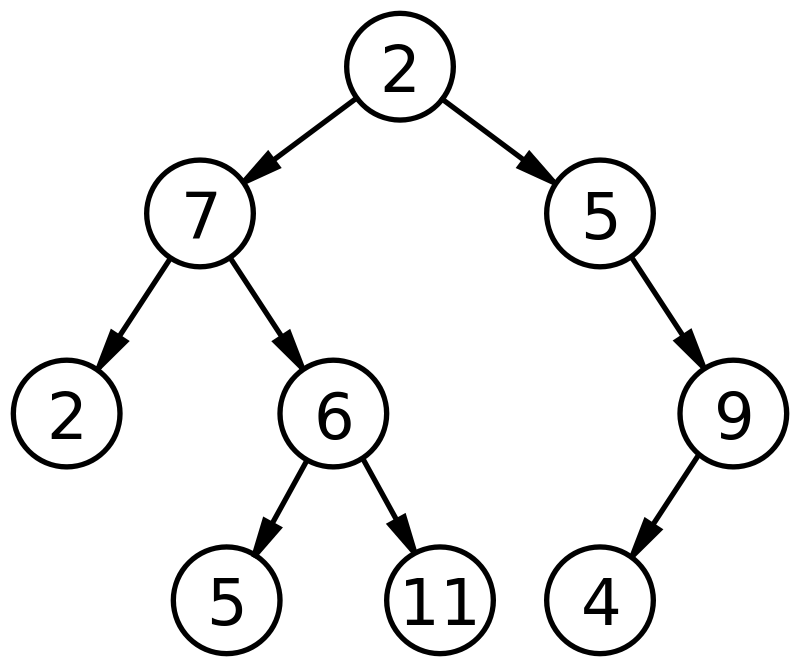
資源
從上圖中,根節點 2 有兩個子節點(或子節點),7 和 5。7 稱為左子節點,5 稱為右子節點。 這樣,每個子節點都充當其他幾個節點的父節點,共同代表二叉樹。
查看:二叉樹的類型
二叉樹中使用的術語
節點:樹中終止點的基本表示。
根節點:二叉樹的最頂層節點。
父節點:如果一個節點通過邊連接到另一個節點,則稱為父節點。 在二叉樹中,一個父節點最多可以有 2 個子節點。
子節點:如果一個節點有一個前任,它被稱為子節點。
葉節點:沒有任何子節點的節點稱為葉節點。
節點深度:它是從根節點到要測量深度的特定節點的距離。
樹的高度:它是從根節點到葉節點的最長距離。
這些是二叉樹的一些基本術語。 有了對二叉樹的基本了解,讓我們繼續討論二叉樹的進步,即二叉搜索樹。
另請閱讀:二分搜索算法:函數、收益、時間和空間複雜性
什麼是二叉搜索樹
顧名思義,二叉搜索樹或 BST 是用於排序、檢索和搜索數據的樹。 它也是一種非線性數據結構,其中節點按特定順序排列。 因此,它也被稱為“有序二叉樹”。 它具有以下屬性:
- 節點的左子樹的節點僅小於該節點的鍵。
- 節點的右子樹具有僅大於該節點的鍵的節點。
- 每個節點都有不同的鍵,並且在二叉搜索樹中不允許重複。
- 左右子樹也必須是二叉搜索樹。
讓我們可視化這個概念,以清楚地了解二叉搜索樹。
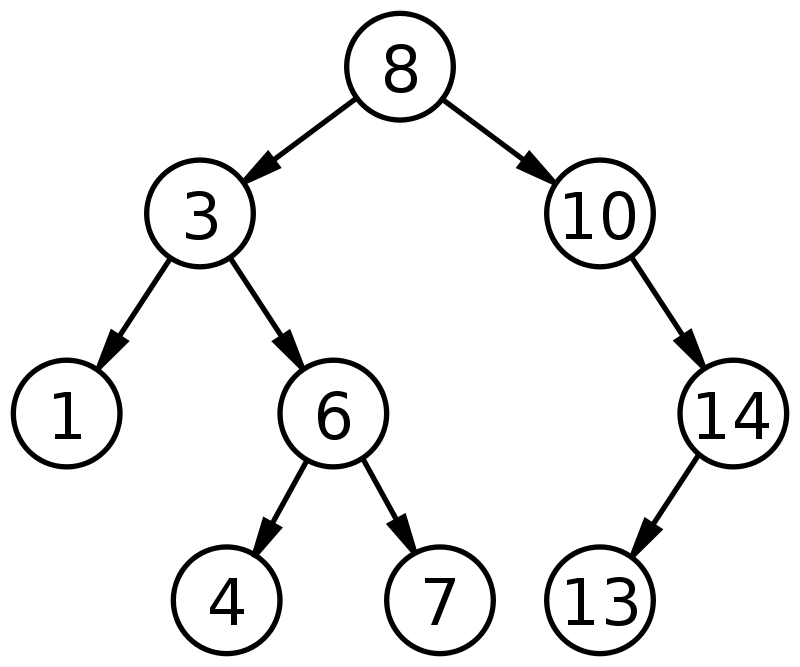
資源
在上圖中,我們看到根節點的值為 8。進一步觀察,觀察到左子樹中的所有值都小於根節點的值,並且右子樹中的所有值都有大於根節點的值。 此外,值得注意的是,二叉搜索樹中的每個值都是唯一的,並且沒有重複項。 因此,驗證了上述二叉搜索樹的性質。

在另一個例子中,我們看到雖然左子樹和右子樹是二叉搜索樹,但在整個樹中具有唯一值。 左子樹的葉節點的值為 12,大於根節點的值為 12。因此,這不滿足 BST 的性質,因此它不是二叉搜索樹。
BST 中的搜索操作 –
考慮具有下面給出的值的二叉搜索樹。 讓我們了解如何執行搜索操作以從二叉搜索樹中得到 9。
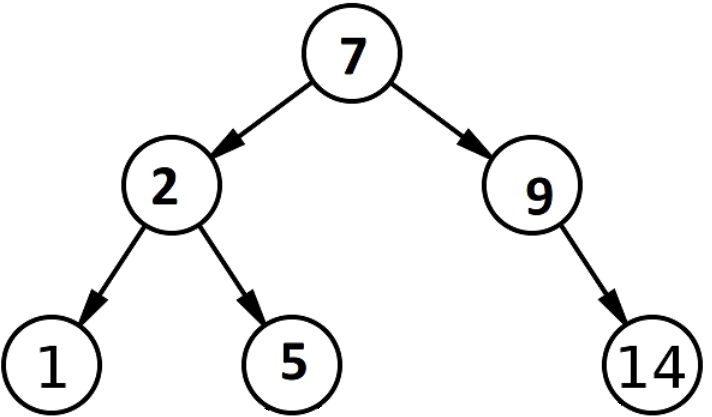
資源
為了執行二分查找,我們首先將所有整數排列在一個有序數組中。 這稱為搜索空間。 該搜索空間應由兩個指針組成,稱為開始指針和結束指針。 上面給出的二叉搜索樹的數組表示為:
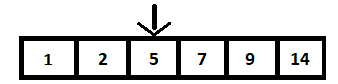
第一步是計算數組的中間值,並將其與要搜索的值(在我們的例子中為 9)進行比較。 這是通過計算 n/2 來完成的,其中 n 是數組 (BST) 中的元素總數,為 6。因此,第 3 個元素是中間元素,即 5。
現在中間元素與 9 比較,因為它不等於(更大),所以搜索操作將在右邊的數組上執行。 這樣,搜索操作就減少了一半,如下圖:
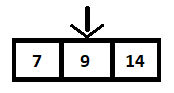
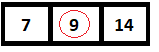
下一步,計算中間元素,發現是9,與我們要搜索的元素相匹配。
二叉樹與二叉搜索樹 -
現在我們對二叉樹和二叉搜索樹都有基本的了解,讓我們快速總結一下它們之間的一些區別。
| 比較基礎 | 二叉樹 | 二叉搜索樹 |
| 定義 | 二叉樹是一種非線性數據結構,其中一個節點可以有 0、1 或 2 個節點。 單獨地,每個節點由左指針、右指針和數據元素組成。 | 二叉搜索樹是具有結構化節點組織的有組織的二叉樹。 每個子樹也必須具有該特定結構。 |
| 結構 | 樹中的節點沒有必要的組織結構。 | 特定節點的左子樹的值應小於該節點,右子樹的值應大於該節點。 |
| 執行的操作 | 可以進行的操作有刪除、插入和遍歷 | 由於這些是排序的二叉樹,它們用於快速高效的二叉搜索、插入和刪除。 |
| 類型 | 有幾種類型。 最常見的是完全二叉樹、完全二叉樹、擴展二叉樹 | 最受歡迎的是 AVL 樹、Splay 樹、探戈樹、T 型樹。 |
結論
因此,我們推斷,儘管二叉樹和二叉搜索樹都具有具有節點集合的共同層次結構,但它們在應用上存在一些差異。 二叉樹是具有簡單規則的基本結構,即沒有父節點必須有超過 2 個子節點,而二叉搜索樹是二叉樹的變體,遵循特定的節點組織順序。
如果您想了解二叉樹與二叉搜索樹,請查看 IIIT-B 和 upGrad 的數據科學 PG 文憑,該文憑專為在職專業人士而設,提供 10 多個案例研究和項目、實用的實踐研討會、行業指導專家,與行業導師一對一,400 多個小時的學習和頂級公司的工作協助。
從世界頂級大學在線學習數據科學課程。 獲得行政 PG 課程、高級證書課程或碩士課程,以加快您的職業生涯。
我們如何遍歷二叉搜索樹?
不像數組、鍊錶、堆棧和隊列等線性數據結構,我們只能以一種方式遍歷數據結構,二叉搜索樹讓我們可以自由地以多種方式遍歷它。 最流行的樹遍歷如下:在中序遍歷中,我們首先遍歷樹的左節點,然後是樹的根節點,最後是樹的右節點。 我們在所有子樹中也遵循相同的方式。 在前序遍歷中,我們首先遍歷樹的根節點,然後分別遍歷左右節點。 我們在所有子樹中也遵循相同的方式。 在後序遍歷中,我們首先分別遍歷樹的左右節點,最後遍歷樹的根節點。 我們在所有子樹中也遵循相同的方式。
BST 的優點和缺點是什麼?
以下是二叉搜索樹的優點和缺點。 優點是 - 插入、刪除和查找等操作可以在 O(log n) 時間內執行,其中 n 是節點數。 BST 中的所有元素都已排序,因此我們可以通過簡單地使用中序遍歷輕鬆地遍歷 BST。 BST 可以有效地用於設計內存分配器以加快內存塊的搜索過程。 二叉搜索樹的最大缺點是我們必須始終使用平衡的 BST,例如 AVL 和紅黑樹,因為如果我們不使用平衡的 BST,我們的樹操作將不會在對數時間內執行。
區分完全二叉樹和完全二叉樹。
完全二叉樹是所有節點的子節點都在 0 到 2 之間的二叉樹。換句話說,除了葉節點之外,所有節點都至少有 2 個子節點的二叉樹稱為完全二叉樹。 另一方面,完全二叉樹是一棵二叉樹,其中每個節點都被完全填滿(正好是兩個子節點),並且葉子節點盡可能位於左側。
