貝葉斯統計和模型：解釋

貝葉斯技術是一種用於數據分析和參數估計的統計方法。 這種方法基於貝葉斯定理。

貝葉斯統計遵循一個獨特的原則，其中它有助於使用統計模型確定觀察到和未觀察到的參數的聯合概率分佈。 在這種情況下，統計知識對於解決分析問題至關重要。

自從托馬斯·貝葉斯在 1770 年代引入貝葉斯定理以來，它一直是統計學中不可或缺的工具。 貝葉斯模型是頻率論模型的經典替代品，因為最近的統計創新幫助突破了許多行業的里程碑，包括醫學研究、理解網絡搜索和處理自然語言（自然語言處理）。

例如，阿爾茨海默氏症是一種眾所周知的疾病，隨著年齡的增長會帶來漸進的風險。 然而，借助貝葉斯定理，醫生可以估計一個人未來患阿爾茨海默氏症的概率。 它也適用於一個人在晚年容易患上的癌症和其他與年齡有關的疾病。

頻繁統計與貝葉斯統計

頻繁統計與貝葉斯統計一直是初學者的爭議話題和噩夢，兩者都難以在兩者之間進行選擇。 在 20 世紀初，貝葉斯統計經歷了不信任和接受問題。 然而，隨著時間的推移，人們意識到貝葉斯模型的適用性及其產生的準確解決方案。

以下是常見的統計數據以及與之相關的複雜性：

頻繁統計

它是統計學界廣泛使用的推理方法。 它分析是否發生了事件（作為假設提及）。 它還估計了在實驗期間發生的事件的概率。 重複實驗直到達到預期的結果。

它們的分佈樣本是實際大小的，實驗理論上可以無限次重複。 這是一個示例，顯示瞭如何使用頻繁的統計數據來研究拋硬幣。

• 拋硬幣一次正面朝上的可能性是 0.5 (1/2)。
• 磁頭數表示實際獲得的潛在客戶數。
• 實際正面數量與預期正面數量之間的差異將隨著投擲次數的增加而增加。

所以在這裡，結果取決於實驗重複的次數。 這是頻繁統計的一個主要缺點。

與它的設計和解釋技術相關的其他缺陷在 20 世紀變得明顯，當時頻繁的統計數據應用於數值模型達到了頂峰。

頻繁統計的局限性

頻繁統計的三大缺陷如下：

1. 變量 p 值

在具有定義端點的實驗中，針對具有固定大小的樣本測量的 p 值會隨著端點和样本大小的任何變化而變化。 它導致單個數據的兩個 p 值不正確。

2. 置信區間不一致

CI（置信區間）完全取決於樣本量。 它使停止潛力無關緊要。

3. CI 的估計值

置信區間不是概率分佈，它們的參數值只是估計值，而不是實際值。

以上三個原因催生了將概率應用於統計問題的貝葉斯方法。

貝葉斯統計的誕生

托馬斯·貝葉斯牧師在 1763 年撰寫的論文中首次提出了貝葉斯統計方法。這種方法由理查德·普賴斯（Richard Price）發表，作為一種基於過去預測未來事件的逆概率策略。

該方法基於下面解釋的貝葉斯定理：

貝葉斯定理

Renyi 的概率公理檢查條件概率，其中事件A和事件B發生的可能性是依賴的或有條件的。 基本條件概率可以寫成：

事件 B 發生的概率取決於事件 A。

上述等式是貝葉斯規則的基礎，貝葉斯定理的數學表達式表明：

這裡，∩表示交集。

貝葉斯規則可以寫成：

貝葉斯規則是貝葉斯統計的基礎，其中統計模型中特定參數的可用信息與收集的數據進行比較和更新。

背景知識表示為先驗分佈，然後將其與觀察或收集的數據作為似然函數進行比較和研究，以找出後驗分佈。

這種後驗分佈用於對未來事件進行預測。

貝葉斯方法的應用取決於以下參數：

1. 定義先驗模型和數據模型
2. 做出相關推論
3. 審查和簡化模型

什麼是貝葉斯神經網絡？

貝葉斯神經網絡 (BNN) 是您在使用統計方法擴展標準網絡並更改後驗推理以跟踪過度擬合時創建的網絡。 由於它是貝葉斯方法，因此存在與神經網絡參數相關的概率分佈。

它們用於解決沒有可用數據自由流動的複雜問題。 貝葉斯神經網絡有助於控制分子生物學和醫學診斷等領域的過度擬合。

人們可以考慮問題答案的整個分佈，而不僅僅是使用貝葉斯神經網絡的一種可能性。 它們幫助您確定模型選擇/比較並解決涉及正則化的問題。

貝葉斯統計提供了數學工具來合理化和更新有關新數據或科學證據的主觀知識。 與頻繁統計方法不同，它的功能基於概率取決於在相同條件下重複事件的頻率的假設。

簡而言之，貝葉斯技術是個人假設和觀點的延伸。 貝葉斯模型使其更有效的關鍵方面是它理解個人根據他們收到的信息類型的不同意見。

然而，隨著新證據和數據的出現，個體有一個收斂點，即貝葉斯推理。 這種合理的更新是貝葉斯統計的特點，使其在分析問題上更加有效。

這裡，當事件發生沒有希望時應用概率 0，當確定事件會發生時應用概率 1。 介於 0 和 1 之間的概率為其他潛在結果提供了空間。

現在應用貝葉斯規則來實現貝葉斯推理，從而從模型中獲得更好的推理。

您如何應用貝葉斯規則來獲得貝葉斯推理？

考慮方程：

P(θ|D) = P(D|θ.)P(θ) / P(D)

P(θ) 表示先驗分佈，

P(θ|D) 表示後驗信念，

P(D) 代表證據，

P(D|θ) 表示可能性。

貝葉斯推理的主要目標是提供一種合理且數學上準確的方法，用於將信念與證據混合以獲得更新的後驗信念。 當生成新數據時，後驗信念可以用作先驗信念。 因此，貝葉斯推理有助於在貝葉斯規則的幫助下不斷更新信念。

考慮相同的拋硬幣示例，貝葉斯模型通過新的拋硬幣將過程從之前的信念更新為後置信念。 貝葉斯方法給出以下概率。

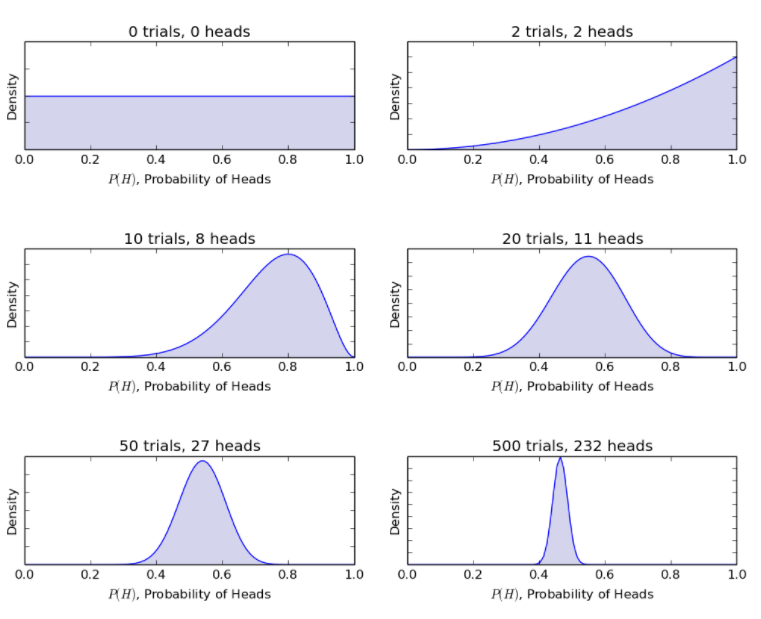
資源

因此，貝葉斯模型允許將具有有限信息的不確定場景合理化為具有大量數據的更明確的場景。

貝葉斯模型和頻率模型之間的顯著差異

頻繁統計

貝葉斯統計

目標被認為是一個點估計，而 CI

目標被認為是後驗分佈

該程序從觀察開始

該過程從先驗分佈開始

每當進行新的觀察時，頻率論方法都會重新計算現有模型。

每當進行新的觀察時，後驗分佈（意識形態/假設）都會更新

示例：均值估計、t 檢驗和 ANOVA。

示例：估計高密度區間的均值和重疊的後驗分佈。

貝葉斯統計的優勢

• 它提供了一種有機而簡單的方法，將預先設想的信息與具有科學證據的堅實框架相結合。 有關參數的過去信息可用於形成先驗分佈以供將來調查。 推論符合貝葉斯定理。
• 貝葉斯模型的推論在邏輯上和數學上是準確的，而不是粗略的假設。 無論樣本大小如何，準確度都保持不變。
• 貝葉斯統計遵循似然原理。 當兩個不同的樣本對於一個信念 θ 有一個共同的似然函數時，關於這個信念的所有推論應該是相似的。 經典統計技術不遵循似然原則。
• 貝葉斯分析的解決方案很容易解釋。
• 它為分層模型和不完整數據問題等各種模型提供了有利的平台。 借助其他數值技術，可以虛擬跟踪所有參數模型的計算。

貝葉斯模型在歷史上的成功應用

貝葉斯方法在二戰期間有很多成功的應用。 下面列出了其中的一些：

• 俄羅斯統計學家Andrey Kolmogorov成​​功地使用貝葉斯方法提高了俄羅斯火砲的效率。
• 貝葉斯模型被用來破解德國 U 型船的密碼。
• 出生於法國的美國數學家伯納德·考普曼（Bernard Koopman）借助貝葉斯模型攔截無線電傳輸，幫助盟軍確定了德國 U 型船的位置。

如果您想了解有關貝葉斯統計的更多信息，請參閱 upGrad 的機器學習和雲高級認證，通過現實生活中的行業項目和案例研究來了解基本概念。 為期 12 個月的課程由 IIT Madras 提供，支持自主學習。

聯繫我們了解更多詳情。