機器學習中的貝葉斯定理:簡介、如何應用和示例
已發表: 2021-02-04目錄
簡介:什麼是貝葉斯定理?
貝葉斯定理以英國數學家托馬斯·貝葉斯的名字命名,他在決策理論(涉及概率的數學領域)廣泛工作。 貝葉斯定理也廣泛用於機器學習,它是一種簡單、有效的方法來準確地預測類別。 計算條件概率的貝葉斯方法用於涉及分類任務的機器學習應用程序。
貝葉斯定理的簡化版本,稱為樸素貝葉斯分類,用於減少計算時間和成本。 在本文中,我們將帶您了解這些概念並討論貝葉斯定理在機器學習中的應用。
加入來自世界頂級大學的在線機器學習課程——碩士、高級管理人員研究生課程和 ML 和 AI 高級證書課程,以加快您的職業生涯。
為什麼在機器學習中使用貝葉斯定理?
貝葉斯定理是一種確定條件概率的方法,即在另一個事件已經發生的情況下,一個事件發生的概率。 因為條件概率包括額外的條件——換句話說,更多的數據——它可以促成更準確的結果。
因此,條件概率是確定機器學習中準確預測和概率的必要條件。 鑑於該領域在各個領域變得越來越普遍,了解貝葉斯定理等算法和方法在機器學習中的作用非常重要。
在我們進入定理本身之前,讓我們通過一個例子來理解一些術語。 假設書店經理有關於他的顧客年齡和收入的信息。 他想知道圖書銷售如何分佈在三個年齡段的客戶中:青年(18-35 歲)、中年(35-60 歲)和老年人(60 歲以上)。

讓我們將我們的數據稱為 X。在貝葉斯術語中,X 稱為證據。 我們有一些假設 H,其中我們有一些屬於某個 C 類的 X。
我們的目標是確定給定 X 的假設 H 的條件概率,即 P(H | X)。
簡單來說,通過確定 P(H | X),我們得到 X 屬於 C 類的概率,給定 X。X 具有年齡和收入的屬性——例如,26 歲,收入為 2000 美元。 H 是我們的假設,即客戶會購買這本書。
密切關注以下四個術語:
- 證據——如前所述,P(X) 被稱為證據。 在這種情況下,這只是客戶年滿 26 歲並賺取 2000 美元的概率。
- 先驗概率——P(H),稱為先驗概率,是我們假設的簡單概率——即客戶將購買一本書。 基於年齡和收入的任何額外輸入都不會提供此概率。 由於計算是用較少的信息完成的,因此結果不太準確。
- 後驗概率– P(H | X) 被稱為後驗概率。 這裡,P(H | X) 是給定 X 的顧客購買一本書 (H) 的概率(他 26 歲,收入 2000 美元)。
- 似然性——P(X | H) 是似然概率。 在這種情況下,假設我們知道客戶會購買這本書,似然概率是客戶年齡為 26 歲且收入為 2000 美元的概率。
鑑於這些,貝葉斯定理指出:
P(H | X) = [ P(X | H) * P(H) ] / P(X)
注意定理中上述四個項的出現——後驗概率、似然概率、先驗概率和證據。
閱讀:樸素貝葉斯解釋
如何在機器學習中應用貝葉斯定理
樸素貝葉斯分類器是貝葉斯定理的簡化版本,被用作分類算法,以準確和快速地將數據分類為各種類別。
讓我們看看如何將樸素貝葉斯分類器用作分類算法。
- 考慮一個一般的例子:X 是一個由“n”個屬性組成的向量,即 X = {x1, x2, x3, ..., xn}。
- 假設我們有“m”類 {C1, C2, ..., Cm}。 我們的分類器必須預測 X 屬於某個類別。 提供最高後驗概率的類將被選為最佳類。 所以在數學上,分類器將預測類別 Ci iff P(Ci | X) > P(Cj | X)。 應用貝葉斯定理:
P(Ci | X) = [ P(X | Ci) * P(Ci) ] / P(X)
- P(X) 與條件無關,對於每個類都是常數。 所以為了最大化 P(Ci | X),我們必須最大化 [P(X | Ci) * P(Ci)]。 考慮到每個類別的可能性相同,我們有 P(C1) = P(C2) = P(C3) ... = P(Cn)。 所以最終,我們只需要最大化 P(X | Ci)。
- 由於典型的大型數據集可能具有多個屬性,因此對每個屬性執行 P(X | Ci) 操作的計算成本很高。 這就是類條件獨立性的用武之地,以簡化問題並降低計算成本。 通過類條件獨立性,我們的意思是我們認為屬性的值有條件地相互獨立。 這就是樸素貝葉斯分類。
P(Xi | C) = P(x1 | C) * P(x2 | C) *… * P(xn | C)
現在很容易計算較小的概率。 這裡需要注意一件重要的事情:由於 xk 屬於每個屬性,我們還需要檢查我們正在處理的屬性是categorical還是Continuous 。
- 如果我們有一個分類屬性,事情就更簡單了。 我們可以只計算由屬性 k 的值 xk 組成的類 Ci 的實例數,然後將其除以類 Ci 的實例數。
- 如果我們有一個連續屬性,考慮到我們有一個正態分佈函數,我們應用以下公式,均值 ? 和標準差?:
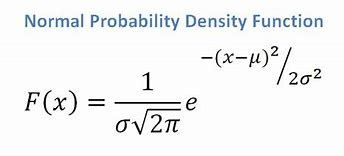

資源
最終,我們將有 P(x | Ci) = F(xk, ?k, ?k)。
- 現在,我們有了對每個類 Ci 使用貝葉斯定理所需的所有值。 我們預測的類將是實現最高概率 P(X | Ci) * P(Ci) 的類。
示例:對書店的客戶進行預測性分類
我們有來自書店的以下數據集:
| 年齡 | 收入 | 學生 | 信用評級 | 買書 |
| 青年 | 高的 | 不 | 公平的 | 不 |
| 青年 | 高的 | 不 | 優秀 | 不 |
| 中年 | 高的 | 不 | 公平的 | 是的 |
| 高級的 | 中等的 | 不 | 公平的 | 是的 |
| 高級的 | 低的 | 是的 | 公平的 | 是的 |
| 高級的 | 低的 | 是的 | 優秀 | 不 |
| 中年 | 低的 | 是的 | 優秀 | 是的 |
| 青年 | 中等的 | 不 | 公平的 | 不 |
| 青年 | 低的 | 是的 | 公平的 | 是的 |
| 高級的 | 中等的 | 是的 | 公平的 | 是的 |
| 青年 | 中等的 | 是的 | 優秀 | 是的 |
| 中年 | 中等的 | 不 | 優秀 | 是的 |
| 中年 | 高的 | 是的 | 公平的 | 是的 |
| 高級的 | 中等的 | 不 | 優秀 | 不 |
我們有年齡、收入、學生和信用等級等屬性。 我們的類 buys_book 有兩個結果:Yes 或 No。
我們的目標是根據以下屬性進行分類:
X = {年齡 = 青年,學生 = 是,收入 = 中等,credit_rating = 一般}。
如前所述,為了最大化 P(Ci | X),我們需要在 i = 1 和 i = 2 時最大化 [ P(X | Ci) * P(Ci) ]。
因此,P(buys_book = yes) = 9/14 = 0.643
P(buys_book = no) = 5/14 = 0.357
P(年齡=青年|購買書=是)= 2/9 = 0.222
P(年齡 = 青年 | 購買書 = 否) =3/5 = 0.600
P(收入 = 中等 | 購買書 = 是)= 4/9 = 0.444
P(收入 = 中等 | 購買書 = 否)= 2/5 = 0.400
P(學生 = 是 | 購買書 = 是)= 6/9 = 0.667
P(學生 = 是 | 購買書 = 否)= 1/5 = 0.200
P(credit_rating = fair | buys_book = yes) = 6/9 = 0.667
P(credit_rating = fair | buys_book = no) = 2/5 = 0.400
使用上面計算的概率,我們有
P(X | buys_book = 是) = 0.222 x 0.444 x 0.667 x 0.667 = 0.044
相似地,
P(X | buys_book = no) = 0.600 x 0.400 x 0.200 x 0.400 = 0.019
Ci 哪個類提供最大 P(X|Ci)*P(Ci)? 我們計算:
P(X | buys_book = 是)* P(buys_book = 是) = 0.044 x 0.643 = 0.028
P(X | buys_book = no)* P(buys_book = no) = 0.019 x 0.357 = 0.007

比較以上兩者,由於 0.028 > 0.007,樸素貝葉斯分類器預測具有上述屬性的客戶會購買一本書。
結帳:機器學習項目的想法和主題
貝葉斯分類器是一個好方法嗎?
機器學習中基於貝葉斯定理的算法提供了與其他算法相當的結果,貝葉斯分類器通常被認為是簡單的高精度方法。 但是,應注意貝葉斯分類器特別適用於類條件獨立性假設有效的情況,而不是適用於所有情況。 另一個實際問題是獲取所有概率數據可能並不總是可行的。
結論
貝葉斯定理在機器學習中有許多應用,特別是在基於分類的問題中。 在機器學習中應用這一系列算法需要熟悉諸如先驗概率和後驗概率等術語。 在本文中,我們討論了貝葉斯定理的基礎知識,它在機器學習問題中的應用,並通過一個分類示例進行了工作。
由於貝葉斯定理是機器學習中基於分類的算法的重要組成部分,因此您可以了解有關upGrad 機器學習和 NLP 高級證書課程的更多信息。 本課程的設計考慮到對機器學習感興趣的各種學生,提供 1-1 指導等等。
為什麼我們在機器學習中使用貝葉斯定理?
貝葉斯定理是一種計算條件概率的方法,即如果另一個事件之前發生過,則另一個事件發生的可能性。 條件概率可以通過包含額外條件(換句話說,更多數據)來產生更準確的結果。 為了在機器學習中獲得正確的估計和概率,需要條件概率。 鑑於該領域在廣泛領域的日益普及,理解貝葉斯定理等算法和方法在機器學習中的重要性至關重要。
貝葉斯分類器是一個不錯的選擇嗎?
在機器學習中,基於貝葉斯定理的算法產生的結果與其他方法相當,貝葉斯分類器被廣泛認為是簡單的高精度方法。 但是,重要的是要記住,貝葉斯分類器最好在類條件獨立的條件正確時使用,而不是在所有情況下。 另一個考慮是獲得所有可能性數據可能並不總是可能的。
貝葉斯定理如何實際應用?
貝葉斯定理根據與之相關或可能相關的新證據來計算發生的可能性。 該方法還可用於查看假設的新信息如何影響事件的可能性,假設新信息是真實的。 以從一副 52 張牌中選出的一張牌為例。 這張牌成為國王的概率是 4 除以 52,即 1/13,或大約 7.69%。 請記住,套牌包含四張國王。 假設顯示所選卡是面卡。 因為一副牌中有 12 張面牌,所以選擇的牌是 K 的概率是 4 除以 12,即大約 33.3%。
