什么是贝叶斯思维？ 引言与定理

英国统计学家和哲学家托马斯·贝叶斯在 1700 年代给出的统计定理仍然是世界各地科学家和分析师的指路明灯。 今天，贝叶斯思想在医学、科学、技术和其他几个学科中得到应用，并继续强烈影响我们的世界观和由此产生的行动。

托马斯的贝叶斯想法非常简单。 根据贝叶斯，假设成立的概率取决于两个条件：它基于我们已经知道的（先验知识）的合理程度以及它与新证据的匹配程度。 因此，贝叶斯思维不同于传统的假设检验，因为前者在得出结论之前包括先验知识。

考虑到初步介绍，让我们深入了解贝叶斯统计的更多细节。

贝叶斯统计

简单来说，贝叶斯统计将概率应用于统计问题，以根据新数据的证据更新先前的信念。 概率表示对特定事件的相信程度。

相信程度可以基于基于个人假设或先前实验结果的关于事件的先前知识。 贝叶斯统计使用贝叶斯定理来计算概率。 反过来，贝叶斯定理描述了基于新证据和与事件相关的先验信息的事件的条件概率。

考虑到这一点，在深入理解贝叶斯定理之前，让我们复习一下条件概率的基本概念。

条件概率

条件概率可以定义为基于先前事件或结果发生的事件或结果的可能性。 它是通过将先前事件的概率乘以后续或条件事件的概率来计算的。

让我们看一个例子来更好地理解这个概念。

• 事件A是计划外出野餐。 这家人有 80% 的机会去野餐。
• 事件B是一家人出去野餐的那天会下雨。 天气预报说野餐当天有 60% 的概率会下雨。
• 因此，家庭去野餐并且下雨的概率（P）计算如下：

P（野餐和雨）= P（雨|野餐）P（野餐）= (0.60) * (0.80) = 0.48

在上面的例子中，条件概率着眼于两个事件 A 和 B 的相互关系，即家人去野餐并且同一天也下雨的概率。

因此，条件概率与无条件概率不同，因为后者指的是事件发生的可能性，无论是否发生任何其他事件或事件或是否存在任何其他条件。

条件概率的公式

条件概率的公式来自概率乘法规则：

P (A 和 B) 或 P (AUB) = P ( B 给定 A) 或 P (B | A) * P (A)

上式中，P（A和B）是联合概率，指的是两个或多个事件同时发生的可能性。 它也写成 P(A,B)。

下面是如何从乘法规则推导出条件概率方程：

第一步：写下乘法规则。

P (A 和 B) = P (B | A) * P (A)

第 2 步：将等式两边除以 P (A)。

P (A 和 B) / P (A) = P (B | A) * P (A) / P (A)

第三步：取消等式右边的P(A)。

P (A 和 B) / P (A) = P (B | A)

第 4 步：重写方程。

P (A 和 B) = P (B | A) / P (A)

因此，条件概率的公式如下：

P (A 和 B) = P (B | A) / P (A)

贝叶斯定理

使用贝叶斯定理，我们可以根据新的相关证据更新我们的信念和信念。 例如，如果我们试图计算某个人患癌症的概率，我们通常会假设它是患癌症的人口百分比。 但是，如果我们引入额外的证据，例如所讨论的人是一个经常吸烟的人，我们可以更新我们的看法（以及因此概率），因为如果一个人是吸烟者，患癌症的概率会更高。 因此，我们利用我们的先验知识和额外的证据来改进我们的估计。

贝叶斯定理的公式

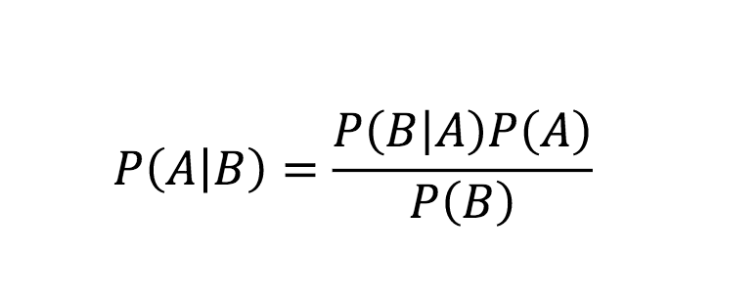
资源

上述等式是贝叶斯规则。 现在，让我们看看贝叶斯定理方程的逐步推导。

第 1 步：考虑两个事件，A 和 B。A 是我们要计算其概率的事件，B 是与 A 相关的附加证据。

第二步：写出事件 A 和 B 的联合概率和条件概率之间的关系。

P (A,B) = P (A | B) * P(B) = P (B,A) = P (B | A) * P(A)

第三步：设置两个条件概率项相等。

P (A | B) * P(B) = P (B | A) * P(A)

第 4 步：将等式两边除以 P (B)。

P (A | B) * P(B) / P (B) = P (B | A) * P(A) / P (B)

步骤 5：取消等式左侧的 P (B)。

P (A | B) = P (B | A) * P(A) / P (B)

因此，我们得到贝叶斯定理的公式如下：

P (A | B) = P (B | A) * P(A) / P (B)

理解贝叶斯定理方程中的项

P (A | B) = P (B | A) * P(A) / P (B)

• P (A | B)称为后验概率或我们试图估计的概率。 基于前面的例子，后验概率将是这个人患有癌症的概率，假设这个人是一个经常吸烟的人。
• P (B | A)被称为似然性，指的是在给定我们初始假设的情况下检测到额外证据的概率。 在上面的例子中，可能性是这个人是吸烟者的概率，假设这个人患有癌症。
• P (A)是先验概率或我们假设的概率，没有任何额外的证据或信息。 在上面的例子中，先验概率是患癌症的概率。
• P (B)是观察证据的边际可能性或总概率。 在上述示例的上下文中，边际可能性是吸烟者的概率。

一个简单的例子来理解贝叶斯定理

使用前面示例中的一些假设数字，我们将看到应用贝叶斯定理的效果。

假设得癌症的概率是0.06，即6%的人得癌症。 现在，假设成为吸烟者的概率是 0.20 或 20% 的人是吸烟者，30% 的癌症患者是吸烟者。 因此，P（吸烟者 | 癌症）= 0.30。

最初，患癌症的概率仅为 0.06（之前）。 但是使用新的证据，我们可以计算出 P (Cancer | Smoker) = P ((Smoker | Cancer) * P (Cancer)) / P (Smoker) = (0.30*0.06) / (0.20) = 0.09。

从世界顶级大学在线学习数据科学课程。 获得行政 PG 课程、高级证书课程或硕士课程，以加快您的职业生涯。

前进之路：掌握数据科学或机器学习职业的统计概念

upGrad 的高等教育技术学习平台以其丰富的课程和沉浸式学习体验影响了全球超过 500,000 名在职专业人士。 upGrad 的行业相关课程在 85 多个国家/地区拥有 40,000 多名学习者，保证能在您选择的领域推动您的职业发展。

数据科学理学硕士课程为期 18 个月，传授统计、预测分析、机器学习、大数据分析、数据可视化等方面的关键技能。

节目亮点：

• 利物浦约翰摩尔斯大学硕士学位和班加罗尔 IIIT 执行 PGP
• 500 多个小时的内容、60 多个案例研究和项目、20 多个现场会议、14 多种编程语言和工具
• 行业网络、疑难解答会议和学习支持

机器学习和深度学习高级证书课程是一门为期 6 个月的严格课程，提供同行交流机会、实践项目、行业指导和 360 度职业帮助。

节目亮点：

• 来自 IIIT 班加罗尔的声望认可
• 240 多个小时的内容，5 个以上的案例研究和项目，24 多个现场会议，涵盖 12 种编程语言、工具和库
• 1:8 小组辅导课程和 1:1 行业专家辅导课程

结论

贝叶斯思维支撑着人类思维、探究和信念的几个领域，尽管我们大多数人都没有意识到这一点。 从癌症筛查和全球变暖到货币政策和风险评估和保险，贝叶斯思维是基础。 即使是著名的英国数学家艾伦·图灵也被认为在第二次世界大战期间采用贝叶斯方法破解了德国的谜密码。

注册 upGrad并进一步了解关键统计概念等等！