数据结构中的树：每个数据科学家都应该知道的 8 种树

介绍

在计算领域，数据结构是指数据在磁盘上的排列方式，便于存储和显示。 它们属于数据科学领域，预计该领域将成为 2021 年有利可图的职业选择。基于对未来几年的预测，大规模深度学习模型和下一代智能设备将为未来这个部门。

因此，获得数据结构的知识对于在技术进步中找到合适的职业至关重要。 根据 2021 年数据科学行业的预测，美国和印度将在其 2,50,000 多家公司中雇佣大约 50,000 名数据科学家和 300,000 名数据分析师。 [1]

数据结构用于设计信息分配、管理和检索的路径。 数据结构对于起草和提高整体处理数据的效率尤其必要。 他们通过对数据进行分组和组织来管理数据，以有效地促进信息交换。

数据结构中的树

“树”是一种 ADT（抽象数据类型），其数据分配遵循分层模式。 本质上，树是通过边连接的多个节点的集合。 这些“树”形成了类似于树的数据结构设计，其中“根”节点通向“父”节点，最终通向“子”节点。 连接是用称为“边缘”的线进行的。

“叶子”节点是没有其他子节点源自它们的端点。 由于其排列的非线性特性，数据结构中的树起着至关重要的作用。 这可以在搜索期间实现更快的响应时间，并在整个设计阶段提供便利。

数据结构中的树类型

下面深入解释数据结构中的各种类型的树：

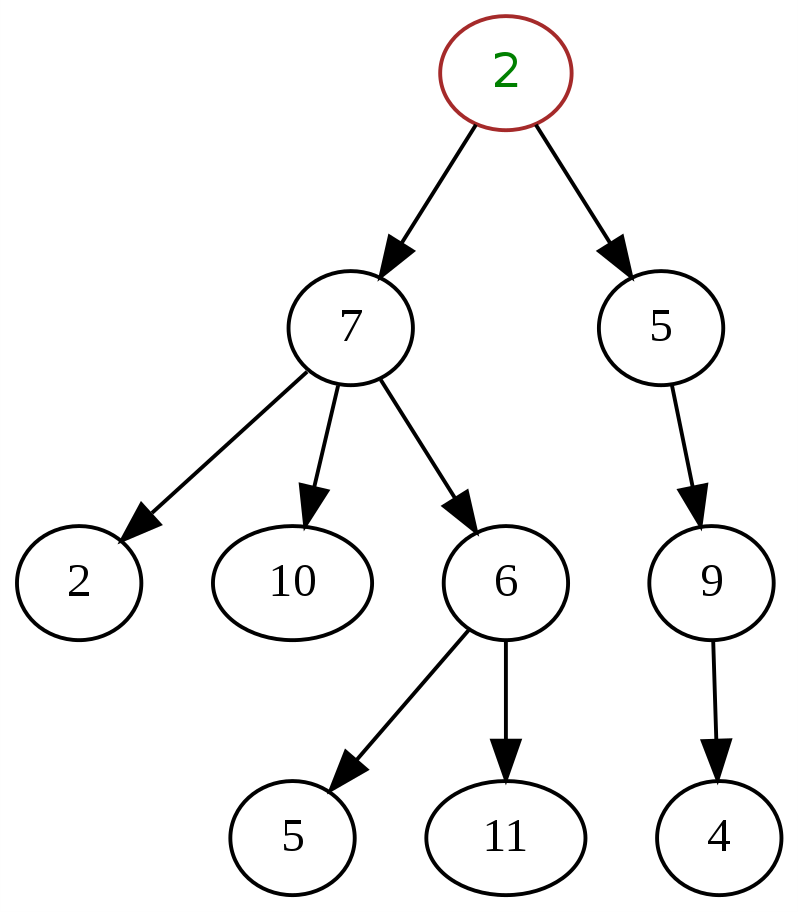
1. 一般树

一般树的特点是对节点可以拥有的子节点数量没有任何规范或限制。 任何具有层次结构的树都可以归类为一般树。 一个节点可以有多个子节点，并且树的方向可以有任何类型的组合。 节点可以是任何度数，从 0 到 n。

以下是数据结构中通用树的经典示例，顶部的“2”是根节点。

资源

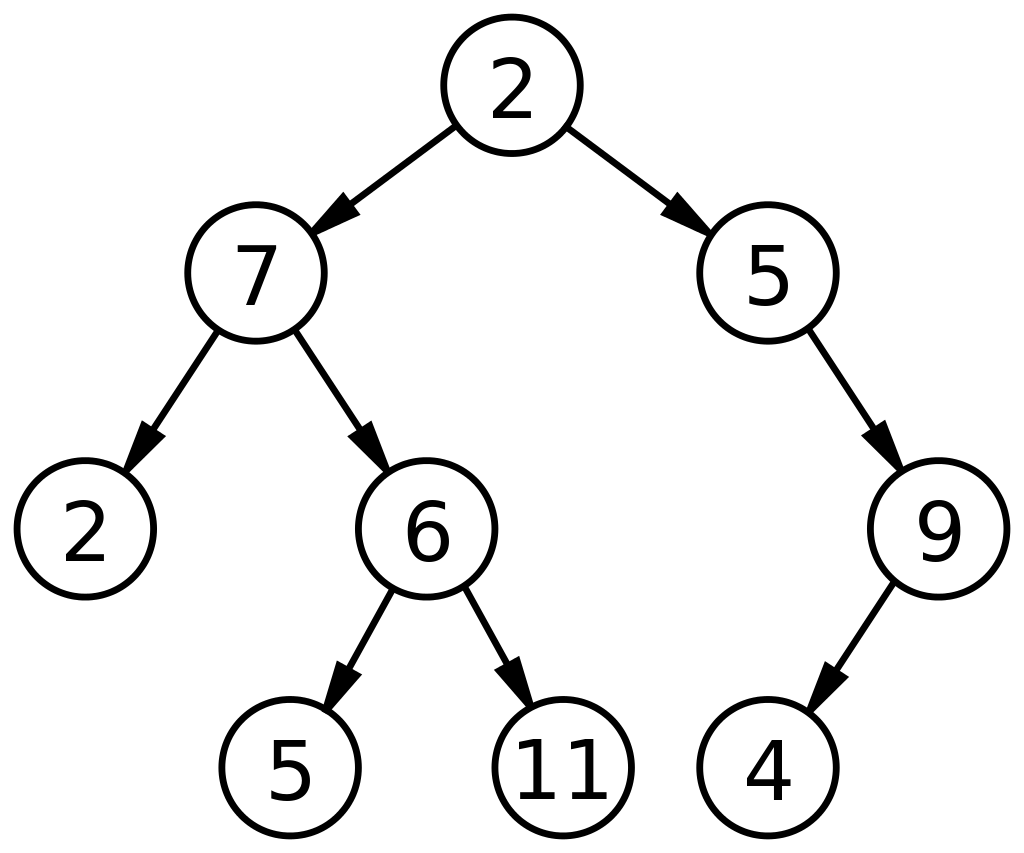
2. 二叉树

正如“二进制”一词所定义的那样，这意味着两个数字，二叉树由可以具有 2 个子节点的节点组成。 二叉树中的任何节点最多可以有 0、1 或 2 个节点。 数据结构中的二叉树是功能强大的 ADT，可以进一步细分为多种类型。 它们主要用于数据结构中，有两个目的：

1. 用于访问节点并标记它们，如二叉搜索树中所观察到的。
2. 用于通过分叉结构表示数据。

下面是数据结构中二叉树的基本图：

资源

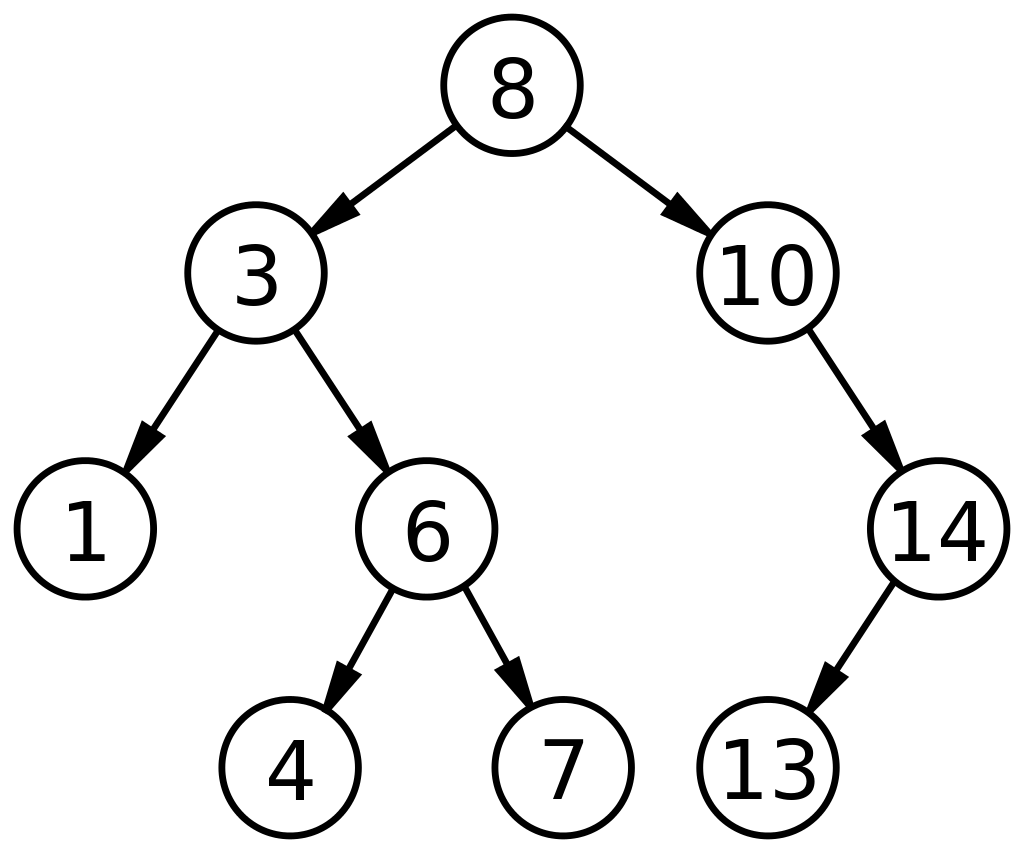
3. 二叉搜索树

二叉搜索树 (BST) 是二叉树的一种独特子类型，其排列方式有助于更快地搜索/查找或添加/删除数据。 BST 由基于三个字段的节点表示定义：数据、其左孩子和右孩子。 BST 的控制因素是：

1. 左侧的每个节点（左子节点）的值都必须小于其父节点。
2. 右侧的每个节点（右子节点）的值都必须高于其父节点。

这种布置将搜索时间减少到线性搜索的一半，如在数组中发现的那样。 因此，与其他 ADT 相比，数据结构中的二叉搜索树广泛适用于搜索和排序。

资源

尽管 BT 和 BST 本质上都是数据结构中的树，但不要被它们名称的相似性所迷惑。 在 upGrad 上详细了解二叉树和二叉搜索树之间的区别。

4.AVL树

AVL 树的名字来源于它的发明者：Adelson-Velsky 和 ​​Landis。 AVL 树的特点是具有自平衡特性。 其根节点的两个子树的高度限制为小于两个。 当高度差增加到 1 以上时，子节点会重新平衡。

AVL 树是高度平衡的，这种重新平衡通过单次或双次旋转发生。 平衡因子是左子树和右子树的高度之差，取值为-1、0、1。

5. 红黑树

这种类型类似于 AVL 树，因为红黑树也是高度平衡的。 它们的不同之处在于它不需要超过两次旋转来平衡它们。 它们包含一个额外的位，用于定义节点的红色或黑色，以确保在删除和插入期间树是平衡的。 在更改期间也会重新绘制红黑色编码，但几乎没有额外的内存成本。

6.张开树

二叉搜索树的另一个子类型，展开树，具有执行旋转操作以调整最近节点的独特属性。 最近访问的节点通过旋转排列为根节点。 它是一棵平衡的树，但不是高度平衡的树。

“展开”的动作是在初始二叉树搜索之后执行的，因为树的旋转是以特定的方式执行的。 每次操作后，树都会旋转以平衡自身，并将搜索到的元素作为根节点排列在顶部。

7. 陷阱

数据结构中的“Treaps”是树和堆的组合。 在 BST 中，左孩子的值必须小于根节点，而右孩子的值必须高于根节点。 在堆数据结构中，根节点的值最小，其子节点（左右）具有较大的值。

因此，treap 以键（类似于 BST）和优先级（如堆）的形式保存值。 优先级最高的节点首先插入到二叉搜索树中，优先级数是独立的随机数。 它们维护一组动态的有序键，并允许在它们的键中进行二进制搜索。

8. B树

作为数据结构中的一种自平衡树，B-Tree 对数据进行排序以允许在对数时间内进行搜索、顺序访问、删除和插入。 与二叉树不同，B 树允许其节点有两个以上的子节点。 它们与读取和写入更大数据块的数据库和文件系统兼容。

数据结构中的 B 树用于较大的存储系统，例如磁盘。 所有的叶子都没有任何信息，它们出现在同一层次内。 B 树的内部节点可以具有由范围限制的可变大小的子节点。

这些是数据结构中的树，由设计数据流的程序员实现。 了解它们的独特特征和应用对于您成为数据科学家的旅程至关重要。 另一种提高自己技能的方法是通过各种需要了解数据结构中的树和其他形式的 ADT 知识的项目进行练习。

为了将您的知识应用于 DS 项目，以下博客链接为初学者提供了 13 个有趣的数据结构项目想法和主题 [2021] 。

结论

学习数据结构中的树之类的概念可能会很棘手，而有志于编程的人需要专家指导来自学。 要了解有关数据结构中树的更多信息，请查看upGrad的在线课程。 软件开发执行 PG 计划 – IIIT-B 和 upGrad 的 DevOps 专业化 DevOps 可以帮助您建立自己的程序员职业生涯。

由于数据结构的熟练程度是编码过程不可或缺的一部分，因此它可以帮助学生成为专家级程序员和软件开发人员。 在未来的几十年里，程序员和数据科学家必将受到需求。

我们在印度有 5 亿互联网用户，产生和消费大量数据，需要雇佣数千名数据科学家来满足需求。 [2]这些数据科学家需要适当的教育和相关的技术专长，才能在该领域寻找工作。

由upGrad和 IIIT-Bangalore 策划的软件开发执行 PG 计划 - 全栈开发专业化，可以帮助您提高个人资料并获得更好的程序员就业机会。