负二项式回归入门:分步指南
已发表: 2022-04-17负二项式回归技术用于对计数变量进行建模。 该方法与多元回归方法几乎相似。 但是,在负二项式回归的情况下,因变量(即 Y)遵循负二项式分布存在差异。 因此,变量的值可以是非负整数,例如 0、1、2。
该方法也是泊松回归的扩展,它在假设均值等于方差时放宽了。 二项式回归的传统模型之一,定义为“NB2”,是基于泊松伽马的混合分布。
泊松回归的方法是通过添加一个伽马噪声变量来推广的。 这个变量的值是平均值,还有一个比例参数是“v”。
以下是负二项式回归的一些示例:
- 学校管理人员进行了一项研究,以研究两所学校的高中生的出勤行为。 可能影响出勤行为的因素可能包括大三学生缺课的天数。 此外,他们注册的计划。
- 来自一项健康相关研究的研究人员对过去 12 个月内有多少老年人到访医院进行了研究。 该研究基于个人特征和老年人购买的健康计划。
负二项式回归示例
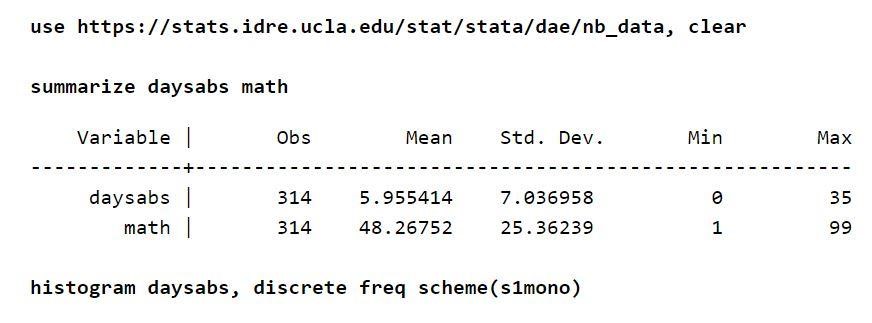
假设有大约 314 名高中学生的出勤表。 数据取自两所城市学校,并存储在名为 nb_data.dta 的文件中。 此示例中有趣的响应变量是缺席天数,即“daysabs”。 存在一个变量“数学”,它定义了每个学生的数学分数。 还有另一个变量是“prog”。 该变量表示学生注册的课程。
资源

每个变量都有大约 314 个观测值。 因此,变量之间的分布也是合理的。 此外,考虑到结果变量,无条件均值低于方差。
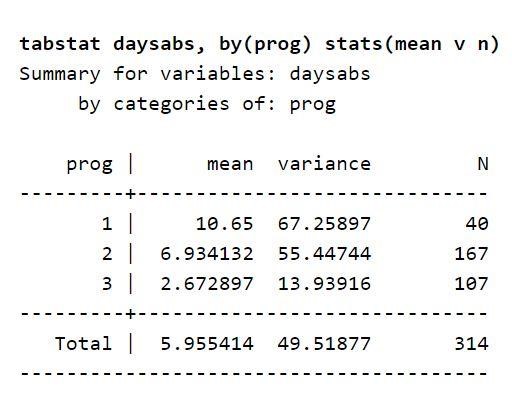
现在,关注数据集中考虑的变量描述。 一个表格列出了学生在每种课程类型中的平均缺勤天数。 这表明变量类型程序可以预测学生缺课的天数。 您也可以使用它来预测结果变量。 这是因为结果变量的平均值因变量 prog 而异。 此外,方差的值高于变量 prog 的每个级别中的值。 这些值称为方差和均值。 现有差异表明存在过度分散,因此使用负二项式模型是合适的。
资源
研究人员可以为此类研究考虑多种分析方法。 这些方法如下所述。 用户可用于分析回归模型的一些分析方法是:
1. 负二项式回归
当存在过度分散的数据时,将使用负二项式回归方法。 这意味着条件方差的值高于或超过条件均值的值。 该方法被认为是从泊松回归方法推广而来的。 这是因为这两种方法的均值结构相同。 但是,负二项式回归中有一个附加参数用于对过度离散进行建模。 当条件分布与结果变量过度分散时,置信区间被认为比激情回归更窄。
2.泊松回归
泊松回归的方法用于计数数据的建模。 许多扩展可用于对泊松回归中的计数变量进行建模。
3.OLS回归
计数变量的结果有时会进行对数变换,然后通过 OLS 回归方法进行分析。 但是,有时存在与 OLS 回归方法相关的问题。 这些问题可能是由于通过考虑零值的对数生成任何未定义值而导致的数据丢失。 此外,它可能是由于缺乏对分散数据的建模而产生的。
4.零膨胀模型
这些类型的模型试图解释模型中所有多余的零。
使用负二项式回归分析
命令“nbreg”用于估计负二项式回归模型。 变量“prog”之前有一个“i”。 “i”的存在表明该变量是类型因子,即分类变量。 这些应作为指标变量包含在模型中。

- 模型的输出以迭代日志开始。 它从泊松模型的拟合开始,然后是零模型,然后是负二项式模型。 该方法使用最大似然估计并不断迭代,直到最终对数的值发生变化。 对数的可能性用于模型的比较。
- 下一个信息在头文件中。
- 标题下方有负二项式回归系数的信息。 为每个变量生成系数以及 p 值、z 分数等误差。 所有系数的置信区间也为 95%。 “数学”变量的系数为 -0.006,表示它具有统计显着性。 结果意味着,如果变量“math”增加一个单位,则缺席天数的预期日志计数将减少 0.006 的值。 此外,指示变量 2. prog 的值是两组(组 2 和参考组)之间日志计数的预期差异。
- 对日志传输过度分散的参数估计已完成,然后以未转换的值显示。 在泊松模型中,该值为零。
- 系数表下方有一个比率检验似然信息。 通过使用“margins”命令可以进一步理解该模型。
在 Python 中进行负二项式回归分析的过程
执行回归过程所需的包需要从 Python 中导入。 下面列出了这些软件包:
- 将 statsmodels.api 导入为 sm
- 将 matplotlib.pyplot 导入为 plt
- 将 numpy 导入为 np
- 从 patsy 导入 dmatrices
- 将熊猫导入为 pd
负二项式回归的注意事项
在应用负二项式回归分析方法时,应考虑一些事项。 这些包括:

- 如果存在小样本,则不推荐使用负二项回归方法。
- 有时存在过多的零点,这可能是过度分散的原因。 由于添加数据生成的过程,可能会生成这些零。 如果出现此类情况,建议使用零膨胀模型的方法。
- 如果数据生成过程不考虑任何零点,那么在这种情况下,建议使用零截断模型的方法。
- 有一个与计数数据相关的曝光变量。 该变量表示事件可能发生的时间。 这个变量是必须纳入负二项式回归模型的。 这是通过 exp() 的选项来完成的。
- 结果变量不能是负二项式回归分析模型中的任何负值。 此外,曝光变量的值不能为 0。
- 命令“glm”也可用于运行负二项式回归分析方法。 这可以通过日志的链接以及二项式系列来完成。
- 获取残差需要命令“glm”。 这是为了检查负二项式回归模型中是否还有其他假设。
- 存在伪 R 平方的各种度量。 但是,每个度量都提供类似于 OLS 回归中 R 平方提供的信息的信息。
结论
文章讨论了负二项式回归这个话题。 我们已经看到,它几乎类似于多元回归的方法,是泊松分布的一种广义形式。 该方法有多种应用。 该技术也可以通过 python 编程语言或 R 应用。
一些案例研究也展示了它在衰老等研究中的应用。 此外,可用于计数数据的经典回归模型是泊松回归、负二项式回归和几何回归。 这些方法属于线性模型家族,几乎包含在所有统计软件包中,例如 R 系统。
如果您想在机器学习方面表现出色并想探索数据领域,那么您可以查看 upGrad 提供的机器学习和人工智能中的 Executive PG Program 课程。 因此,如果您是一名梦想成为机器学习专家的工作专业人士,请来获得在专家手下接受培训的经验。 更多细节可以通过我们的网站获得。 如有任何疑问,我们的团队可以及时为您提供帮助。