你应该知道的 7 个 Python 中最常用的机器学习算法

机器学习是人工智能 (AI) 的一个分支，它处理用于任何数据的计算机算法。 它专注于从输入的数据中自动学习，并通过每次改进先前的预测来为我们提供结果。

Python 中使用的顶级机器学习算法

以下是 Python 中使用的一些顶级机器学习算法，以及代码片段显示了它们的实现和分类边界的可视化。

1. 线性回归

线性回归是最常用的监督机器学习技术之一。 顾名思义，此回归尝试使用线性方程对两个变量之间的关系进行建模，并将该线拟合到观察到的数据。 该技术用于估计真实的连续值，例如总销售额或房屋成本。

最佳拟合线也称为回归线。 它由以下等式给出：

Y = a*X + b

其中 Y 是因变量，a 是斜率，X 是自变量，b 是截距值。 系数 a 和 b 是通过最小化各个数据点与回归线方程之间的距离差的平方得出的。

# 用于简单回归的合成数据集

从 sklearn.datasets 导入 make_regression

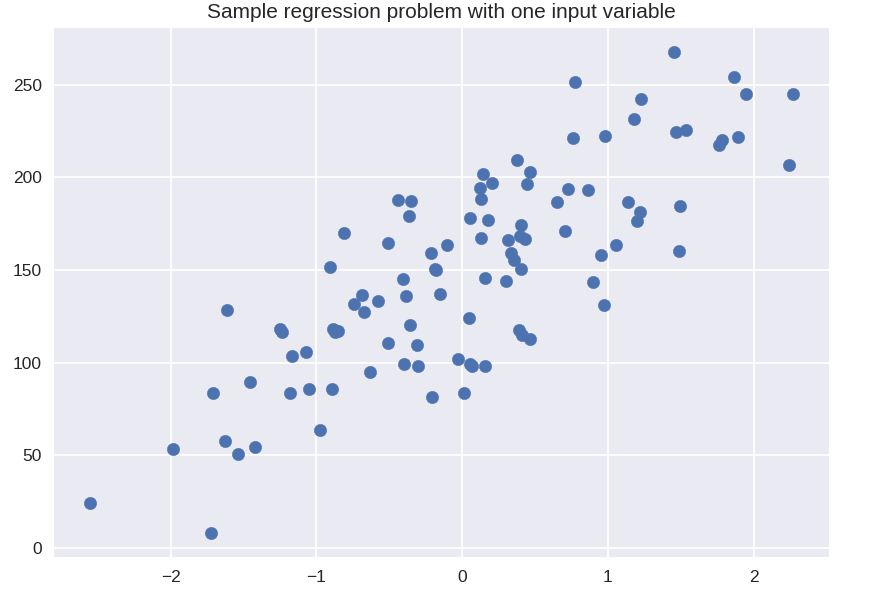
plt.figure()

plt.title('一个输入变量的样本回归问题')

X_R1，y_R1 = make_regression（n_samples = 100，n_features = 1，n_informative = 1，偏差 = 150.0，噪声 = 30，random_state = 0）

plt.scatter(X_R1, y_R1, 标记 = 'o', s = 50)

plt.show()

从 sklearn.linear_model 导入线性回归

X_train，X_test，y_train，y_test = train_test_split（X_R1，y_R1，

随机状态 = 0)

linreg = LinearRegression().fit(X_train, y_train)

print('线性模型系数 (w): {}'.format(linreg.coef_))

print('线性模型截距(b): {:.3f}'z.format(linreg.intercept_))

print('R-squared score (training): {:.3f}'.format(linreg.score(X_train, y_train)))

print('R-squared score (test): {:.3f}'.format(linreg.score(X_test, y_test)))

输出

线性模型系数（w）：[45.71]

线性模型截距（b）：148.446

R平方分数（训练）：0.679

R平方分数（测试）：0.492

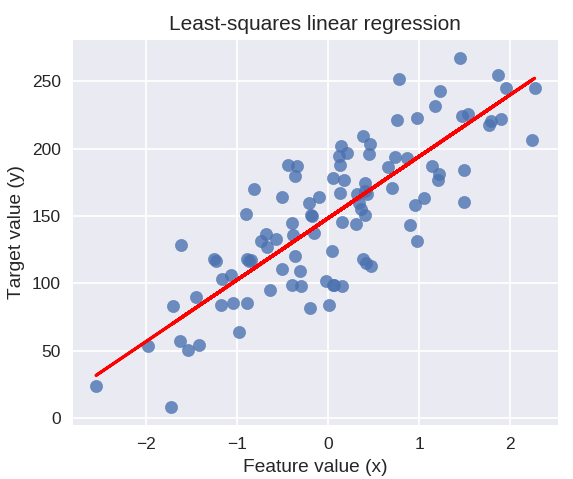
以下代码将在我们的数据点图上绘制拟合回归线。

plt.figure(figsize = (5, 4))

plt.scatter(X_R1, y_R1, marker = 'o', s = 50, alpha = 0.8)

plt.plot(X_R1, linreg.coef_ * X_R1 + linreg.intercept_, 'r-')

plt.title('最小二乘线性回归')

plt.xlabel('特征值(x)')

plt.ylabel('目标值(y)')

plt.show()

准备用于探索分类技术的通用数据集

以下数据将用于展示 Python 机器学习中最常用的各种分类算法。

UCI 蘑菇数据集存储在蘑菇.csv 中。

%matplotlib 笔记本

将熊猫导入为 pd

将 numpy 导入为 np

将 matplotlib.pyplot 导入为 plt

从 sklearn.decomposition 导入 PCA

从 sklearn.model_selection 导入 train_test_split

df = pd.read_csv('readonly/mushrooms.csv')

df2 = pd.get_dummies(df)

df3 = df2.sample(frac = 0.08)

X = df3.iloc[:, 2:]

y = df3.iloc[:, 1]

pca = PCA（n_components = 2）.fit_transform（X）

X_train，X_test，y_train，y_test = train_test_split（pca，y，random_state = 0）

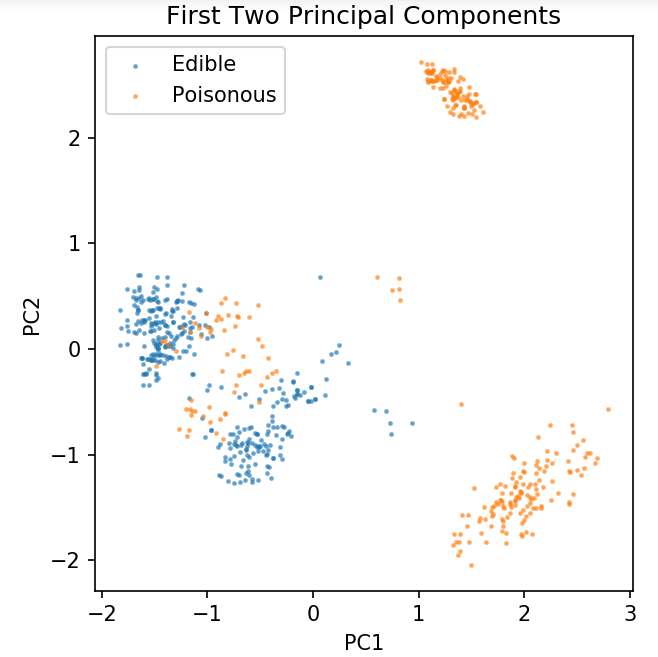
plt.figure(dpi = 120)

plt.scatter(pca[y.values == 0, 0], pca[y.values == 0, 1], alpha = 0.5, label = 'Edible', s = 2)

plt.scatter(pca[y.values == 1, 0], pca[y.values == 1, 1], alpha = 0.5, label = 'Poisonous', s = 2)

plt.legend()

plt.title('蘑菇数据集\n前两个主成分')

plt.xlabel('PC1')

plt.ylabel('PC2')

plt.gca().set_aspect('等于')

我们将使用下面定义的函数来获取我们将在蘑菇数据集上使用的不同分类器的决策边界。

def plot_mushroom_boundary（X，y，fitted_model）：

plt.figure(figsize = (9.8, 5), dpi = 100)

对于 i，枚举中的 plot_type（['Decision Boundary'，'Decision Probabilities']）：

plt.subplot( 1, 2, i + 1 )

mesh_step_size = 0.01 # 网格中的步长

x_min, x_max = X[:, 0].min() – .1, X[:, 0].max() + .1

y_min, y_max = X[:, 1].min() – .1, X[:, 1].max() + .1

xx，yy = np.meshgrid（np.arange（x_min，x_max，mesh_step_size），np.arange（y_min，y_max，mesh_step_size））

如果我 == 0：

Z = 拟合模型预测（np.c_[xx.ravel(), yy.ravel()] ）

别的：

尝试：

Z = 拟合模型.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]

除了：

plt.text(0.4, 0.5, '概率不可用', 水平对齐 = '中心', 垂直对齐 = '中心', 变换 = plt.gca().transAxes, fontsize = 12)

plt.axis('关闭')

休息

Z = Z.reshape(xx.shape)

plt.scatter(X[y.values == 0, 0], X[y.values == 0, 1], alpha = 0.4, label = 'Edible', s = 5)

plt.scatter(X[y.values == 1, 0], X[y.values == 1, 1], alpha = 0.4, label = 'Posionous', s = 5)

plt.imshow（Z，插值='最近'，cmap ='RdYlBu_r'，alpha = 0.15，范围=（x_min，x_max，y_min，y_max），原点='下'）

plt.title(plot_type +'\n'+str(fitted_model).split('(')[0]+'测试精度：'+str(np.round(fitted_model.score(X,y),5)) )

plt.gca().set_aspect('等于');

plt.tight_layout()

plt.subplots_adjust（顶部 = 0.9，底部 = 0.08，wspace = 0.02）

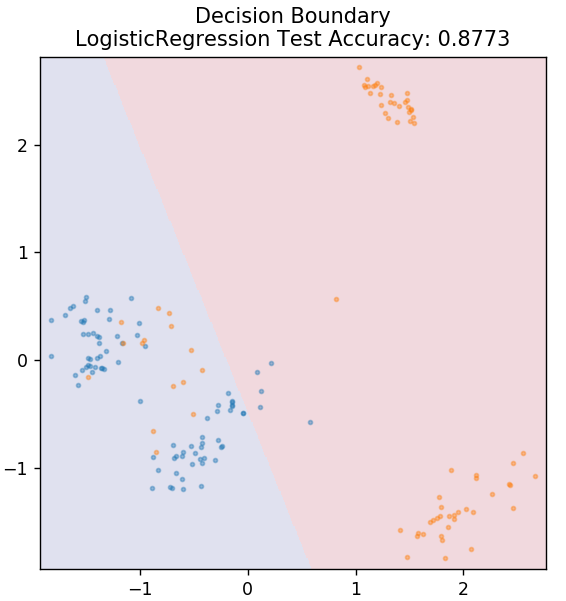
2. 逻辑回归

与线性回归不同，逻辑回归处理离散值的估计（0/1 二进制值、真/假、是/否）。 这种技术也称为 logit 回归。 这是因为它通过使用 logit 函数来训练给定数据来预测事件的概率。 它的值始终介于 0 和 1 之间（因为它正在计算概率）。

结果的对数几率构造为预测变量的线性组合，如下所示：

几率 = p / (1 – p) = 事件发生的概率或事件不发生的概率

ln( 赔率 ) = ln( p / (1 – p) )

logit( p ) = ln( p / (1 – p) ) = b0 + b1X1 + b2X2 + b3X3 + … + bkXk

其中 p 是特征存在的概率。

从 sklearn.linear_model 导入 LogisticRegression

模型 = 逻辑回归（）

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

从世界顶级大学在线获得人工智能认证——硕士、高管研究生课程和 ML 和 AI 高级证书课程，以加快您的职业生涯。

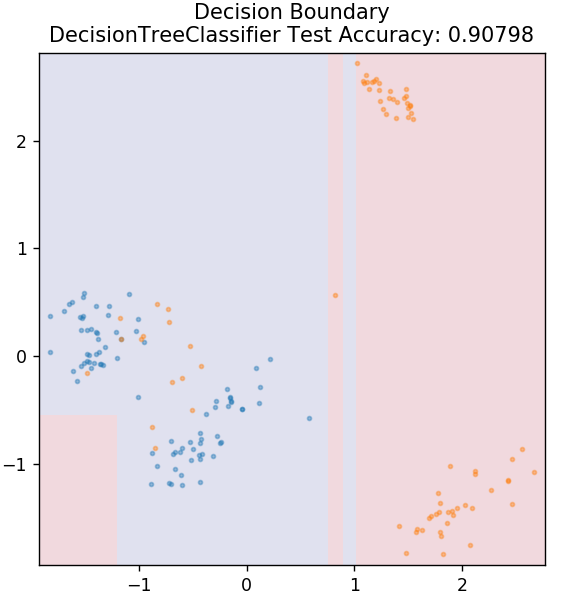
3. 决策树

这是一种非常流行的算法，可用于对数据的连续变量和离散变量进行分类。 在每一步，数据都会根据一些拆分属性/条件拆分为多个同质集。

从 sklearn.tree 导入 DecisionTreeClassifier

模型 = 决策树分类器（最大深度 = 3）

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

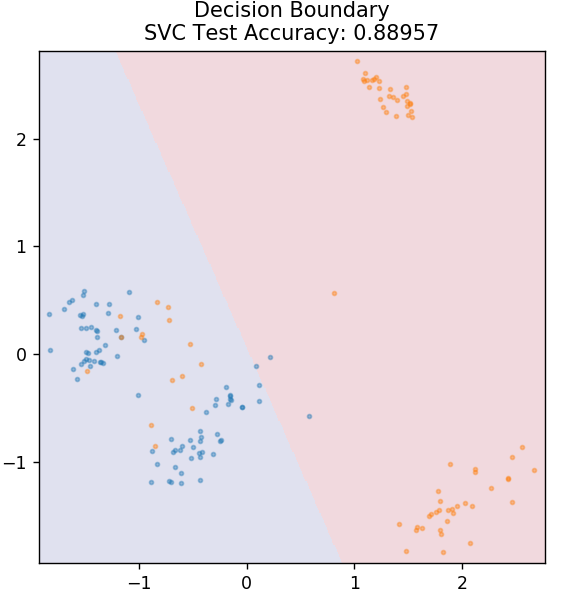
4. 支持向量机

SVM 是支持向量机的缩写。 这里的基本思想是通过使用超平面进行分离来对数据点进行分类。 目标是找出在类或类别的数据点之间具有最大距离（或边距）的超平面。

我们选择平面的方式是为了在未来以最高的置信度对未知点进行分类。 支持向量机的使用非常著名，因为它们提供了高精度，同时占用的计算能力非常少。 SVM 也可用于回归问题。

从 sklearn.svm 导入 SVC

模型= SVC（内核='线性'）

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

结帐： GitHub 上的 Python 项目

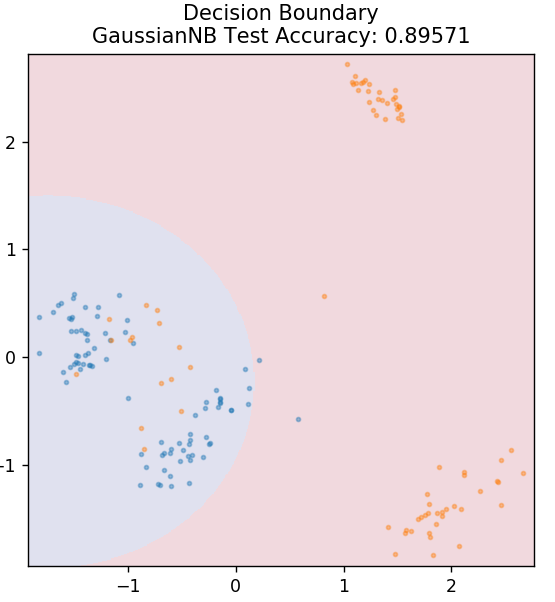
5.朴素贝叶斯

顾名思义，朴素贝叶斯算法是一种基于贝叶斯定理的监督学习算法。 贝叶斯定理使用条件概率根据给定的知识为您提供事件的概率。

在哪里，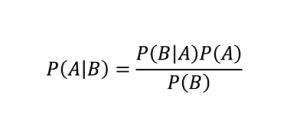

P (A | B)：假设事件 B 已经发生，事件 A 发生的条件概率。 （也称为后验概率）

P(A)：事件 A 的概率。

P(B)：事件 B 的概率。

P (B | A)：假设事件 A 已经发生，事件 B 发生的条件概率。

你问为什么这个算法被命名为 Naive？ 这是因为它假设所有事件的发生都是相互独立的。 所以每个特征分别定义了一个数据点所属的类，它们之间没有任何依赖关系。 朴素贝叶斯是文本分类的最佳选择。 即使是少量的训练数据，它也能很好地工作。

从 sklearn.naive_bayes 导入 GaussianNB

模型 = GaussianNB()

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

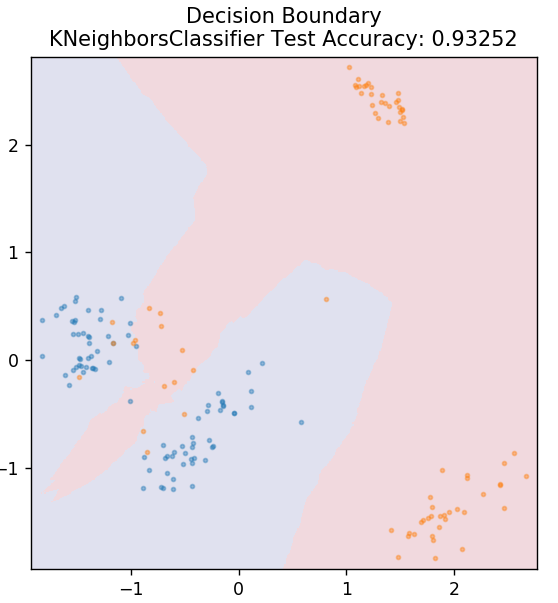
5.KNN

KNN 代表 K-最近邻。 它是一种使用非常广泛的监督学习算法，它根据测试数据与之前分类的训练数据的相似性对测试数据进行分类。 KNN 在训练期间不会对所有数据点进行分类。 相反，它只存储数据集，当它获得任何新数据时，它会根据它们的相似性对这些数据点进行分类。 它通过计算该数据点的 K 个最近邻居（此处为n_neighbors ）的欧几里德距离来实现。

从 sklearn.neighbors 导入 KNeighborsClassifier

模型 = KNeighborsClassifier（n_neighbors = 20）

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

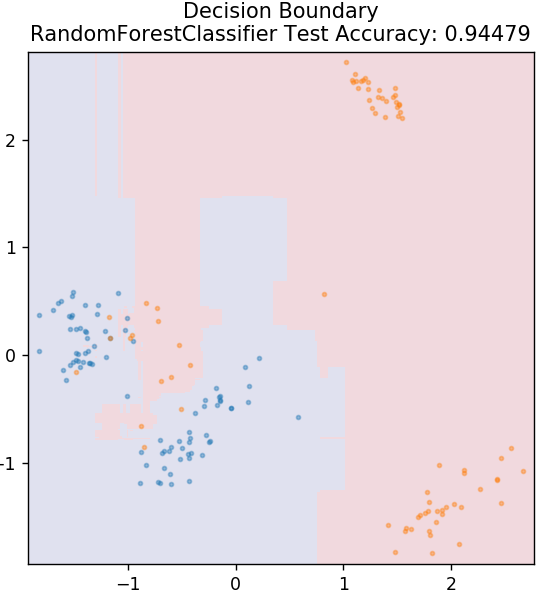
6. 随机森林

随机森林是一种非常简单且多样化的机器学习算法，它使用监督学习技术。 正如您可以从名称中猜到的那样，随机森林由大量决策树组成，充当一个整体。 每个决策树都会计算出数据点的输出类别，并选择多数类别作为模型的最终输出。 这里的想法是，处理相同数据的更多树往往比单个树的结果更准确。

从 sklearn.ensemble 导入 RandomForestClassifier

模型 = RandomForestClassifier()

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

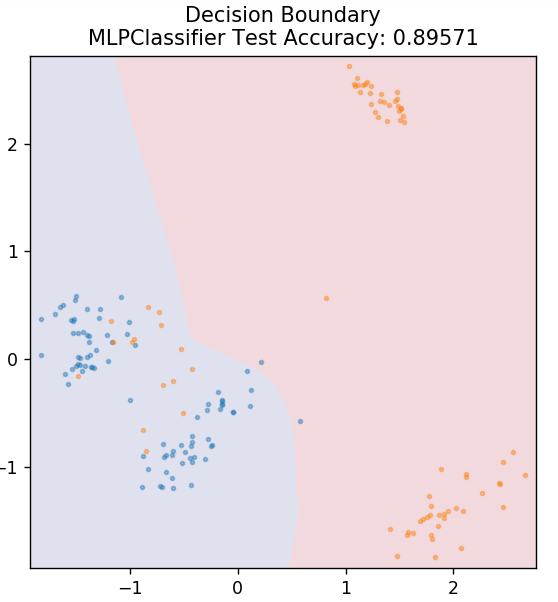
7. 多层感知器

多层感知器（或 MLP）是一种非常迷人的算法，属于深度学习的分支。 更具体地说，它属于前馈人工神经网络 (ANN) 类。 MLP 形成一个由至少三层的多个感知器组成的网络：输入层、输出层和隐藏层。 MLP 能够区分非线性可分的数据。

隐藏层中的每个神经元都使用激活函数进入下一层。 在这里，反向传播算法用于实际调整参数，从而训练神经网络。 它主要用于简单的回归问题。

从 sklearn.neural_network 导入 MLPClassifier

模型 = MLPClassifier()

model.fit(X_train, y_train)

plot_mushroom_boundary（X_test，y_test，模型）

另请阅读： Python 项目理念和主题

结论

我们可以得出结论，不同的机器学习算法会产生不同的决策边界，因此不同的准确性会导致对同一数据集进行分类。

一般来说，没有办法将任何算法声明为所有类型数据的最佳算法。 机器学习需要对各种算法进行严格的试验和错误，以确定分别对每个数据集最有效的方法。 ML 算法的列表显然不会到此结束。 在 Python 的 Scikit-Learn 库中还有大量其他技术等待探索。 继续使用所有这些训练您的数据集，玩得开心！

如果您有兴趣了解有关决策树、机器学习的更多信息，请查看 IIIT-B 和 upGrad 的机器学习和人工智能执行 PG 计划，该计划专为工作专业人士设计，提供 450 多个小时的严格培训、30 多个案例研究和任务、IIIT-B 校友身份、5 个以上实用的实践顶点项目和顶级公司的工作协助。