概率密度函数简介【公式、性质、应用、实例】

概率密度函数 (PDF) 是统计中的表达式，表示离散随机变量的概率分布。 简单来说，概率分布可以定义为随机变量（如股票或 ETF）的结果的可能性。 离散变量与可以确定准确值的连续随机变量相反。

例如，股票市场中的股票价值在离散随机变量中只有两个小数点（例如，65.76），而不是具有任意小数点的连续变量（例如：65.7685434567）。

概率密度函数是一种统计工具，用于确定离散随机变量结果的可能性。 在图表上绘制时，PDF 看起来与钟形曲线相同，其中曲线下的面积代表结果的概率。

当投影为图形模型时，曲线下的面积表示离散随机变量的值将落入的范围。 因此，曲线下的总面积等于变量结果的概率。

概率密度函数可以确定随机变量落在特定值范围内的可能性。

通常，概率密度函数分析与股票市场中特定基金相关的风险和潜在收入。

被视为概率密度函数的函数要满足的条件

与可以具有无限个值的连续变量相比，可以准确测量离散变量的值。 任何函数都应满足以下两个条件才能成为概率密度函数：

• 随机变量的每个可能值的 f(x) 值应为正（非负）。
• 曲线总面积的积分值（随机变量所有可能值的积分）应为 1。

概率密度函数和概率分布函数的区别

随机变量可以有很多值。 对随机变量可能具有的每个可能值的描述称为其概率分布。

概率分布给出了一组结果及其相关概率。 表示连续概率分布的统计函数称为概率密度函数。

还有另一种表示离散概率分布的统计工具，称为概率质量函数。 这详细说明了所有可能的结果及其可能性概率。

概率密度函数的表达式

如果随机变量是离散的，则其概率分布称为概率质量函数，如果是连续变量，则其概率分布称为概率密度函数。

当所讨论的随机变量具有一系列可能值时，使用 PDF。 它们的概率分布用于确定准确值。

让随机变量用X表示。随机变量X的概率密度函数f可以表示为

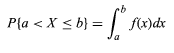
• 随机变量的值介于 a 和 b 之间。
• 如果 X 表示从范围（区间）r 和 s 中选择特定数的概率，则概率密度函数可以表示为

f ( x ) = 1/( s − r ) 对于r < x < s和f ( x ) = 0 对于x < r或x > s 。

• PDF F 表示为：

F ( x ) = P { X ≤ x }

称为 X 的分布函数或累积分布函数。

考虑到随机变量 X 有一个概率分布函数f ( x )，那么 f 和 F 之间的关系可以建立为

F ′(. x ) = f ( x )

离散随机变量的分布函数不同于其概率分布函数。 两者的关系可以表示如下：

随机变量的期望表示为，

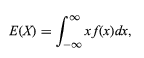
因此，在组合理论的帮助下，可以统一处理所有离散和随机变量。

概率密度函数公式

连续随机变量 X 在某个固定值 x 上的概率始终为 0。在这种情况下，不能使用 P(X = x)。 应确定位于值范围 (a,b) 之间的 X 值。 为了确定相同，使用以下公式。

概率密度函数的性质

例如，取值在 (a,b) 范围内的连续随机变量将通过计算曲线下面积和以 (a) 作为其下限和 (b) 作为其绘制的 X 轴的面积来估计上限。 上述的概率密度函数表示为：

对于所有可能的值，概率密度函数都是正的（非负的）。 这意味着对于每个 x，f(x)≥ 0。 密度曲线和 X 轴（水平轴）之间的面积等于 1。

这也可以表示为：

密度函数曲线在给定范围内是连续的，它是针对一系列连续值或变量域明确定义的。

加入来自世界顶级大学的在线机器学习课程——硕士、高级管理人员研究生课程和 ML 和 AI 高级证书课程，以加快您的职业生涯。

概率密度函数的应用

• 概率密度函数用于大气 NO 浓度水平的年度建模。
• 柴油发动机燃烧建模。
• 在统计学中，概率密度函数用于确定随机变量结果的可能性。

概率密度函数示例

• 示例 1

以下是如何使用概率密度函数 (PDF) 来确定投资者在股票市场中的潜在风险的示例：

首先，PDF 是根据历史信息生成的图形工具。

PDF 最常见的形式是中性投影，其中风险等于各种可能性的回报。 风险承担能力较低的投资者只会获得有限的利润，因此他们处于钟形曲线的左侧。 相反，具有高风险承担能力的投资者可能会获得更高的收益率，因此落在曲线的右侧。

大多数投资者处于平均风险承担能力之下，因此他们占据了曲线的中间。

这有助于根据收到的数据分析投资者的类别。 这有助于股票市场经纪人确定他们的目标客户类别以销售他们的产品。

• 示例 2

概率密度函数的基本应用之一是高斯随机变量，也称为正态随机变量。

在这两种情况下，该图都给出了概率密度函数的钟形曲线。

密度可以表示为

上述密度方程的图表如下所示。

曲线下的面积代表高斯随机变量的实际值。

结论

概率密度函数在机器学习中起着至关重要的作用。 对于着眼于机器学习和人工智能职业的学生，​​我们强烈建议注册 upGrad 的机器学习 IIT 高级证书课程。 该计划是定制的，旨在使高级工作专业人员能够使用云计算技术部署机器学习模型。

该课程由 IIT Madras 的教师和行业专家设计，以使学习过程更加相关和实用。 该计划提供来自印度令人垂涎的排名第一的工程学院的全球认可认证以及 upGrad 的 360 度就业支持。

更重要的是，您有大量机会与 upGrad 的 40,000 多名付费学习者合作开展大型项目。

前往我们的网站开始您的学习之旅！