机器学习中的多元回归简介：完整指南

今天的技术是数据驱动的，这已经不是什么秘密了。 数据可能只是数字的汇编，但可以对其进行有意义的处理，以提取生产力和资源，使企业长期保持竞争力和可持续发展。 碰巧的是，数据分析是从原始信息中得出准确估计的答案。

数据分析是一种涉及统计和逻辑思想的技术，用于审查、处理数据并将其转换为可用形式。 数据分析得出的解决方案用于企业做出重要决策。 数据科学与数据分析一起用于高精度预测未来结果。 这是一个使用科学技术和算法从数据池中获取可行信息的过程。

数据专业人员面临的一个常见问题是如何确定响应变量（用 Y 表示）和解释变量（用 Xi 表示）之间是否存在统计关系。

这个问题的答案是回归分析。 让我们更详细地了解这一点。

什么是回归分析？

回归分析是遵循受控或监督机器学习算法的数据分析中的流行方法之一。 它是一种识别和建立数据变量之间关系的有效技术。

回归分析涉及使用数学策略对可行变量进行分类，以对这些分类变量得出高度准确的结论。

什么是多元回归？

多变量是一种分析多个数据变量的受控或监督机器学习算法。 它是多元回归的延续，涉及一个因变量和许多自变量。 根据自变量的数量预测输出。

多元回归计算出一个公式，该公式解释了变量中存在的因素对其他因素变化的同时响应。 它们用于研究各个领域的数据。 例如，在房地产中，多元回归用于根据位置、房间数量和可用设施等几个因素来预测房屋的价格。

多元回归中的成本函数

当模型的结果偏离观察到的数据时，成本函数会为样本分配成本。 成本函数方程是预测值与实际值之差的平方除以数据集长度的两倍。

这是一个例子：

结果：

资源

如何使用多元回归分析？

多元回归分析涉及的过程包括特征选择、特征工程、特征归一化、选择损失函数、假设分析和创建回归模型。

1. 特征的选择：这是多元回归中最重要的一步。 也称为变量选择，此过程涉及选择可行的变量以建立有效的模型。
2. 特征归一化：这涉及特征缩放以保持流线型分布和数据比率。 这有助于更好的数据分析。 可以根据需要更改所有特征的值。
3. 选择损失函数和假设：损失函数用于预测错误。 当假设预测与实际数字发生变化时，损失函数就会发挥作用。 在这里，假设表示从特征或变量预测的值。
4. 固定假设参数：假设的参数是固定的或设置为使其最小化损失函数并增强更好的预测。
5. 减少损失函数：通过生成专门用于数据集损失最小化的算法来最小化损失函数，这反过来又有助于改变假设参数。 梯度下降是最常用的损失最小化算法。 一旦损失最小化完成，该算法也可以用于其他操作。
6. 分析假设函数：需要分析假设的函数，因为它对于预测值至关重要。 在分析函数之后，然后在测试数据上对其进行测试。

现在让我们看看可以使用多元回归的两种方式。

1. 多元线性回归

多元线性回归类似于简单线性回归，只是在多元线性回归中，多个自变量对因变量有贡献，因此在计算中使用了多个系数。

• 它用于推导多个随机变量之间的数学关系。 它解释了有多少多个自变量与一个因变量相关联。
• 多个自变量的详细信息用于准确预测它们对结果变量的影响。
• 多元线性回归模型以线性形式（直线形式）生成每个数据点的最佳近似关系。
• 多元线性回归模型的方程为：

yi​=β0​+β1​xi1​+β2​xi2​+…+βp​xip​+

对于 i=n 观察，其中：

资源

什么时候可以使用线性回归？

线性回归模型只有在有两个连续变量且一个依赖另一个独立的情况下才可以使用。

自变量用作确定因变量的值或结果的参数。

2. 多元逻辑回归

逻辑回归是一种用于基于多个自变量预测二元结果的算法。 二元结果有两种可能性，或者场景发生（用 1 表示）或者它没有发生（用 0 表示）。

在处理二元数据时使用逻辑回归，即结果（或因变量）是二分法的数据。

逻辑回归可以用在什么地方？

逻辑回归主要用于处理分类问题。 例如，确定电子邮件是否为垃圾邮件以及特定交易是否是恶意的。 在数据分析中，它用于做出有计划的决策，以最大限度地减少损失并增加利润。

当存在一个因变量和多个结果时，使用多变量逻辑回归。 它与逻辑回归的不同之处在于有两个以上的可能结果。

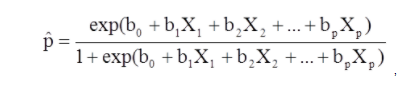
X1 到 Xp 是不同的自变量。

b0 到 bp 是回归系数

多元逻辑回归模型也可以写成不同的形式。 在下面的表格中，结果是结果出现概率的预期对数，

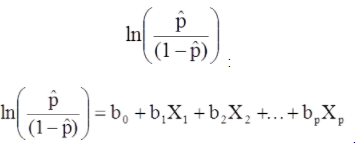
多元逻辑回归模型也可以写成不同的形式。 在下面的表格中，结果是结果出现概率的预期对数。

上式右边类似于线性回归方程，但求出回归系数的方法不同。

多元回归模型中的假设

• 因变量和自变量具有线性关系。
• 自变量之间没有很强的相关性。
• yi 的观察值是从总体中随机且单独地选择的。

多元逻辑回归模型中的假设

• 因变量是名义变量或有序变量。 名义变量有两个或多个类别，没有任何有意义的组织。 序数变量也可以有两个或多个类别，但它们具有结构并且可以排序。
• 可以有单个或多个自变量，可以是有序的、连续的或名义的。 连续变量是在特定范围内可以具有无限值的变量。
• 因变量是互斥且穷举的。
• 自变量之间没有很强的相关性。

多元回归的优点

1. 多元回归帮助我们研究数据集中多个变量之间的关系。
2. 因变量和自变量之间的相关性有助于预测结果。
3. 它是机器学习中最方便、最流行的算法之一。

多元回归的缺点

• 多元技术的复杂性需要复杂的数学计算。
• 解释多元回归模型的输出并不容易，因为损失和错误输出存在不一致。
• 多元回归模型不能应用于较小的数据集； 它们旨在在涉及更大的数据集时产生准确的输出。

如果您想了解有关多元回归和其他复杂数据科学主题的更多信息，upGrad 正是您的解决方案。 我们来自利物浦约翰摩尔斯大学的为期 18 个月的数据科学理学硕士课程涵盖 500 多个严格的学习时间、25 节辅导课程（以 1:8 的方式举行）和 20 多个现场课程。 upGrad 还提供 1:1 教学协助和 360° 职业指导支持，帮助学生转变职业生涯。 学习者可以在全球平台上与超过 40,000 名付费学习者一起利用对等学习，并在六个职能专业领域开展合作项目，以最大限度地提高他们的学习体验。