机器学习中的链式法则导数：解释

机器学习已经发展成为近年来最受关注和研究的领域之一，并且有充分的理由。 机器学习的新模型和应用每天都在被发现，全球的研究人员都在为下一件大事而努力。

因此，来自不同背景的专业人士越来越有兴趣转向机器学习并成为这场正在进行的革命的一部分。 如果您是这样的机器学习爱好者，希望迈出第一步，那么让我们告诉您，首先要了解数学和统计学的基础知识。

与机器学习高度相关的数学中一个重要的主题是导数。 根据您对微积分的基本了解，您会记得任何函数的导数都是该函数的瞬时变化率。 在这篇博客中，我们将深入研究衍生品并探索链式法则。 当我们改变方程中的一些自变量时，我们将看到特定函数的输出如何变化。 借助链式规则导数的知识，您将能够区分在机器学习中肯定会遇到的更复杂的函数。

从世界顶级大学在线获得机器学习认证——硕士、高管研究生课程和 ML 和 AI 高级证书课程，以加快您的职业生涯。

了解链式法则导数

链式法则本质上是一个数学公式，可以帮助您计算复合函数的导数。 复合函数是由两个或多个函数组成的函数。 所以，如果f和g是两个函数，那么链式法则将帮助我们找到复合函数的导数，例如fog或go f。

考虑到复合函数雾，链式法则导数如下所示：

上面的规则也可以写成：

其中函数F是f 和 g的组合，形式为 f(g(x))。

现在，假设我们有三个变量，其中第三个变量 (z) 取决于第二个变量 (y)，而第二个变量又取决于第一个变量 (x)。 在这种情况下，链式规则导数看起来像这样：

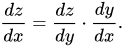在深度学习方面，这也是经常用来解决反向传播问题的公式。 现在，由于我们提到 z 依赖于 y 和 y 依赖于 x，我们可以写成 z = f(y) 和 y = g(x)。 这种替换将以以下方式修改我们的微分方程：

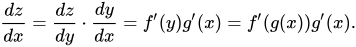现在，让我们看一些链式法则导数的例子，以更好地理解它们背后的数学原理。

链式规则导数的例子和应用

让我们从维基百科中举一个著名的例子来更好地理解链式规则导数。 假设你从天上自由落体。 您在秋季遇到的大气压力会不断变化。 这是一个绘制大气压力随海拔高度变化的图表：

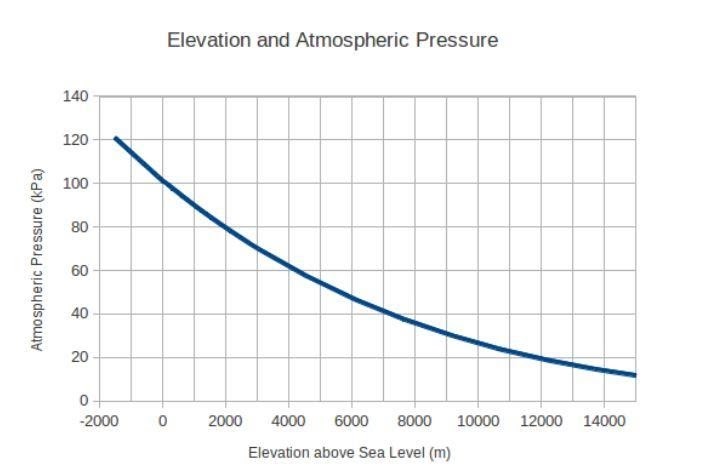
假设你的坠落始于海拔 4000 米。 最初，您的速度为零，由于重力，加速度值为每秒 9.8 米。

现在，让我们将这种情况与之前的链式法则方法进行比较。 在本例中，我们将使用变量“t”来表示时间而不是 x。

然后，变量 y = g(t) 表示自秋季开始以来行进的距离，可以如下给出：

g(t) = 0.5*9.8t^2

并且，海平面的高度可以由变量“h”给出，它等于 400-g(t)。

假设，基于一个模型，我们还可以将任意高度h处的大气压函数写为：

f(h) = 101325 e−0.0001h

现在，您可以根据它们的因变量区分这两个方程，以获得以下结果：

g′(t) = -9.8t,

在这里，g'(t) 告诉您在任何时间t的速度值。

f′(h) = -10.1325e-0.0001h

这里，f'(h) 是大气压相对于高度 h 的变化率。 现在，问题是我们能否将这两个方程结合起来，得出大气压随时间的变化率？ 让我们看看使用链式法则：

我们得到的最后一个方程为我们提供了大气压力相对于自秋天以来经过的时间的变化率。 在机器学习方面，神经网络不断需要关于神经元预测误差的权重更新。 链式法则有助于调整这些权重并使机器学习模型更接近正确的输出。

结论

如您所见，链式法则有很多用途。 尤其是在机器学习或深度学习方面，链式法则在更新神经元的权重和提高模型的整体效率方面有很多用处。

现在您已经了解了链式法则的基础知识，请继续尝试自己解决一些问题。 查找一些复合函数并尝试找到它们的导数。 你练习得越多，你的概念就会越清晰，你就越容易训练你的机器学习模型！ 也就是说，如果您是机器学习爱好者，但在努力迈出该领域的第一步，那么 upGrad 将为您提供支持！

我们的机器学习和人工智能执行 PG 计划与 IIIT-Bangalore 合作提供，为您提供六种行业相关专业的选择。 该课程从底层开始，将您带到顶点，同时为您提供来自行业专家的一对一支持、强大的同龄学生群体以及 360 度的职业支持。