二叉树与二叉搜索树:二叉树和二叉搜索树之间的区别
已发表: 2021-01-21目录
介绍
排序是按系统顺序排列数据以便更有效地分析数据的过程。 识别特定记录的过程称为搜索。 如果数据按特定顺序正确排序,则搜索将成为一项简单而有效的任务。 本文处理最重要的非线性数据结构之一,即树。
树主要用于通过展示元素之间的层次关系来表示数据。 例如,目录、家谱。 从技术上讲,一棵树可以定义为一个或多个节点的有限集合“T”,使得一个节点被指定为树的根,而其他节点被划分为 n>=0 不相交的集合 T1、T2、T3, T4…… Tn 和被称为该根节点的子树或子节点。
什么是二叉树?
二叉树是一种非线性数据结构,其中一个节点可以有 0、1 或 2 个节点。 二叉树中的每个节点都称为父节点或子节点。 二叉树的最高节点称为根节点。 每个父节点最多可以有 2 个子节点,即左子节点和右子节点。
二叉树中的节点具有三个字段:
- 数据元素——它存储节点要存储的数据值。
- 指向左子节点的指针——它存储对左子节点的引用(或地址)。
- 指向右子节点的指针——它存储对右子节点的引用。
这样,几个节点组合在一起就构成了一个二叉树。
二叉树可以表示为:
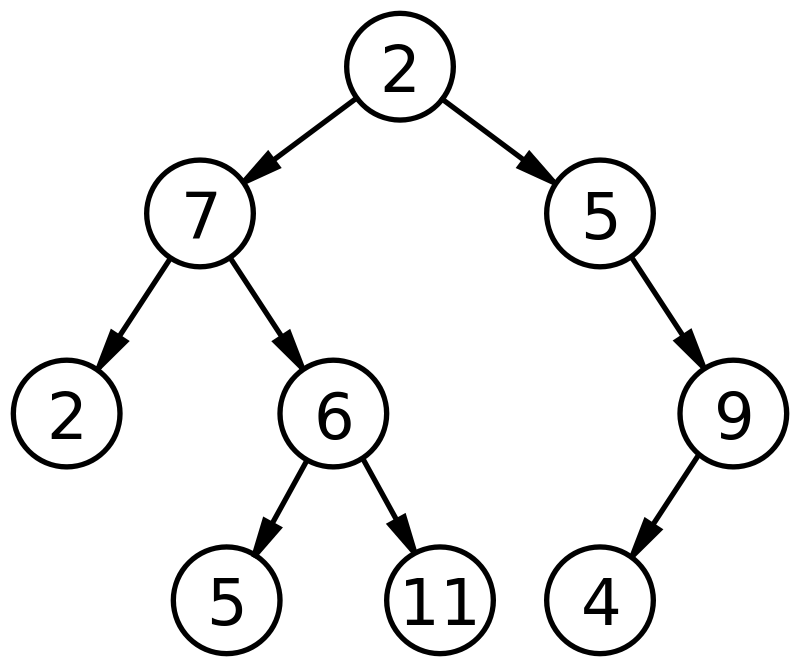
资源
从上图中,根节点 2 有两个子节点(或子节点),7 和 5。7 称为左子节点,5 称为右子节点。 这样,每个子节点都充当其他几个节点的父节点,共同代表二叉树。
查看:二叉树的类型
二叉树中使用的术语
节点:树中终止点的基本表示。
根节点:二叉树的最顶层节点。
父节点:如果一个节点通过边连接到另一个节点,则称为父节点。 在二叉树中,一个父节点最多可以有 2 个子节点。
子节点:如果一个节点有一个前任,它被称为子节点。
叶节点:没有任何子节点的节点称为叶节点。
节点深度:它是从根节点到要测量深度的特定节点的距离。
树的高度:它是从根节点到叶节点的最长距离。
这些是二叉树的一些基本术语。 有了对二叉树的基本了解,让我们继续讨论二叉树的进步,即二叉搜索树。
另请阅读:二分搜索算法:函数、收益、时间和空间复杂性
什么是二叉搜索树
顾名思义,二叉搜索树或 BST 是用于排序、检索和搜索数据的树。 它也是一种非线性数据结构,其中节点按特定顺序排列。 因此,它也被称为“有序二叉树”。 它具有以下属性:
- 节点的左子树的节点仅小于该节点的键。
- 节点的右子树具有仅大于该节点的键的节点。
- 每个节点都有不同的键,并且在二叉搜索树中不允许重复。
- 左右子树也必须是二叉搜索树。
让我们可视化这个概念,以清楚地了解二叉搜索树。
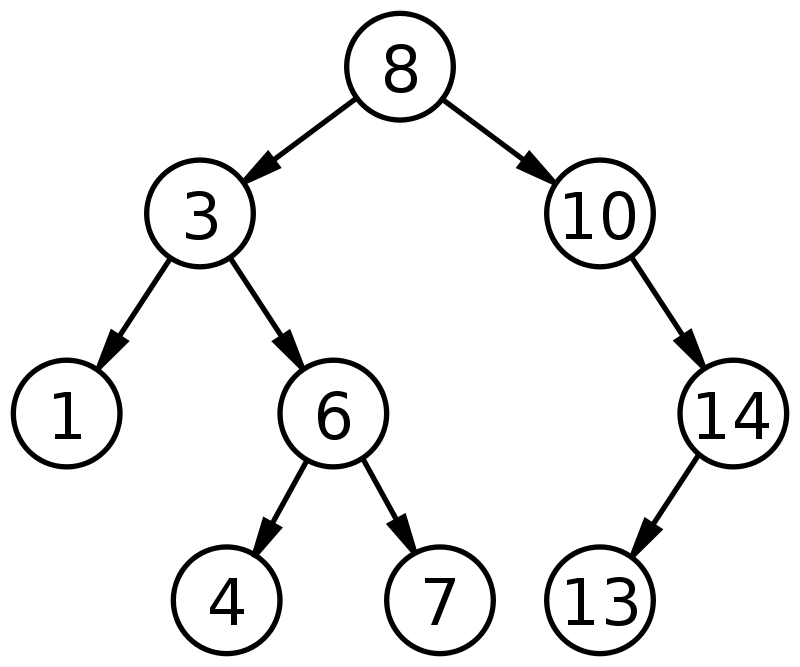
资源
在上图中,我们看到根节点的值为 8。进一步观察,观察到左子树中的所有值都小于根节点的值,并且右子树中的所有值都有大于根节点的值。 此外,值得注意的是,二叉搜索树中的每个值都是唯一的,并且没有重复项。 因此,验证了上述二叉搜索树的性质。

在另一个例子中,我们看到虽然左子树和右子树是二叉搜索树,但在整个树中具有唯一值。 左子树的叶节点的值为 12,大于根节点的值为 12。因此,这不满足 BST 的性质,因此它不是二叉搜索树。
BST 中的搜索操作 –
考虑具有下面给出的值的二叉搜索树。 让我们了解如何执行搜索操作以从二叉搜索树中得到 9。
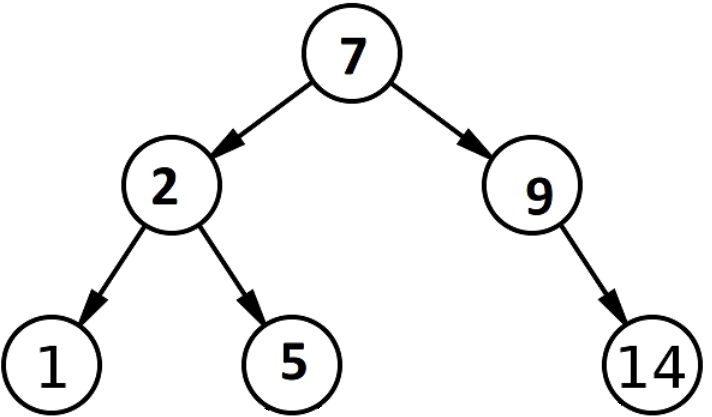
资源
为了执行二分查找,我们首先将所有整数排列在一个有序数组中。 这称为搜索空间。 该搜索空间应由两个指针组成,称为开始指针和结束指针。 上面给出的二叉搜索树的数组表示为:
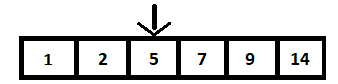
第一步是计算数组的中间值,并将其与要搜索的值(在我们的例子中为 9)进行比较。 这是通过计算 n/2 来完成的,其中 n 是数组 (BST) 中的元素总数,为 6。因此,第 3 个元素是中间元素,即 5。
现在中间元素与 9 比较,因为它不等于(更大),所以搜索操作将在右边的数组上执行。 这样,搜索操作就减少了一半,如下图:
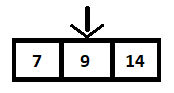
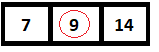
下一步,计算中间元素,发现是9,与我们要搜索的元素相匹配。
二叉树与二叉搜索树 -
现在我们对二叉树和二叉搜索树都有基本的了解,让我们快速总结一下它们之间的一些区别。
| 比较基础 | 二叉树 | 二叉搜索树 |
| 定义 | 二叉树是一种非线性数据结构,其中一个节点可以有 0、1 或 2 个节点。 单独地,每个节点由左指针、右指针和数据元素组成。 | 二叉搜索树是具有结构化节点组织的有组织的二叉树。 每个子树也必须具有该特定结构。 |
| 结构 | 树中的节点没有必要的组织结构。 | 特定节点的左子树的值应小于该节点,右子树的值应大于该节点。 |
| 执行的操作 | 可以进行的操作有删除、插入和遍历 | 由于这些是排序的二叉树,它们用于快速高效的二叉搜索、插入和删除。 |
| 类型 | 有几种类型。 最常见的是完全二叉树、完全二叉树、扩展二叉树 | 最受欢迎的是 AVL 树、Splay 树、探戈树、T 型树。 |
结论
因此,我们推断,尽管二叉树和二叉搜索树都具有具有节点集合的共同层次结构,但它们在应用上存在一些差异。 二叉树是具有简单规则的基本结构,即没有父节点必须有超过 2 个子节点,而二叉搜索树是二叉树的变体,遵循特定的节点组织顺序。
如果您想了解二叉树与二叉搜索树,请查看 IIIT-B 和 upGrad 的数据科学 PG 文凭,该文凭专为在职专业人士而设,提供 10 多个案例研究和项目、实用的实践研讨会、行业指导专家,与行业导师一对一,400 多个小时的学习和顶级公司的工作协助。
从世界顶级大学在线学习数据科学课程。 获得行政 PG 课程、高级证书课程或硕士课程,以加快您的职业生涯。
我们如何遍历二叉搜索树?
不像数组、链表、堆栈和队列等线性数据结构,我们只能以一种方式遍历数据结构,二叉搜索树让我们可以自由地以多种方式遍历它。 最流行的树遍历如下:在中序遍历中,我们首先遍历树的左节点,然后是树的根节点,最后是树的右节点。 我们在所有子树中也遵循相同的方式。 在前序遍历中,我们首先遍历树的根节点,然后分别遍历左右节点。 我们在所有子树中也遵循相同的方式。 在后序遍历中,我们首先分别遍历树的左右节点,最后遍历树的根节点。 我们在所有子树中也遵循相同的方式。
BST 的优点和缺点是什么?
以下是二叉搜索树的优点和缺点。 优点是 - 插入、删除和查找等操作可以在 O(log n) 时间内执行,其中 n 是节点数。 BST 中的所有元素都已排序,因此我们可以通过简单地使用中序遍历轻松地遍历 BST。 BST 可以有效地用于设计内存分配器以加快内存块的搜索过程。 二叉搜索树的最大缺点是我们必须始终使用平衡的 BST,例如 AVL 和红黑树,因为如果我们不使用平衡的 BST,我们的树操作将不会在对数时间内执行。
区分完全二叉树和完全二叉树。
完全二叉树是所有节点的子节点都在 0 到 2 之间的二叉树。换句话说,除了叶节点之外,所有节点都至少有 2 个子节点的二叉树称为完全二叉树。 另一方面,完全二叉树是一棵二叉树,其中每个节点都被完全填满(正好是两个子节点),并且叶子节点尽可能位于左侧。
