贝叶斯统计和模型：解释

贝叶斯技术是一种用于数据分析和参数估计的统计方法。 这种方法基于贝叶斯定理。

贝叶斯统计遵循一个独特的原则，其中它有助于使用统计模型确定观察到的和未观察到的参数的联合概率分布。 在这种情况下，统计知识对于解决分析问题至关重要。

自从托马斯·贝叶斯在 1770 年代引入贝叶斯定理以来，它一直是统计学中不可或缺的工具。 贝叶斯模型是频率论模型的经典替代品，因为最近的统计创新帮助突破了许多行业的里程碑，包括医学研究、理解网络搜索和处理自然语言（自然语言处理）。

例如，阿尔茨海默氏症是一种众所周知的疾病，随着年龄的增长会带来渐进的风险。 然而，借助贝叶斯定理，医生可以估计一个人未来患阿尔茨海默氏症的概率。 它也适用于一个人在晚年容易患上的癌症和其他与年龄有关的疾病。

频繁统计与贝叶斯统计

频繁统计与贝叶斯统计一直是初学者的争议话题和噩梦，两者都很难在两者之间进行选择。 在 20 世纪初，贝叶斯统计经历了不信任和接受问题。 然而，随着时间的推移，人们意识到贝叶斯模型的适用性及其产生的准确解决方案。

以下是常见的统计数据以及与之相关的复杂性：

频繁统计

它是统计学界广泛使用的推理方法。 它分析是否发生了事件（作为假设提及）。 它还估计了在实验期间发生的事件的概率。 重复实验直到达到预期的结果。

它们的分布样本是实际大小的，实验理论上可以无限次重复。 这是一个示例，显示了如何使用频繁的统计数据来研究抛硬币。

• 抛硬币一次正面朝上的可能性是 0.5 (1/2)。
• 磁头数表示实际获得的潜在客户数。
• 实际正面数量与预期正面数量之间的差异将随着投掷次数的增加而增加。

所以在这里，结果取决于实验重复的次数。 这是频繁统计的一个主要缺点。

与它的设计和解释技术相关的其他缺陷在 20 世纪变得明显，当时频繁的统计数据应用于数值模型达到了顶峰。

频繁统计的局限性

频繁统计的三大缺陷如下：

1. 变量 p 值

在具有定义端点的实验中，针对具有固定大小的样本测量的 p 值会随着端点和样本大小的任何变化而变化。 它导致单个数据的两个 p 值不正确。

2. 置信区间不一致

CI（置信区间）完全取决于样本量。 它使停止潜力无关紧要。

3. CI 的估计值

置信区间不是概率分布，它们的参数值只是估计值，而不是实际值。

以上三个原因催生了将概率应用于统计问题的贝叶斯方法。

贝叶斯统计的诞生

托马斯·贝叶斯牧师在 1763 年撰写的论文中首次提出了贝叶斯统计方法。这种方法由理查德·普赖斯（Richard Price）发表，作为一种基于过去预测未来事件的逆概率策略。

该方法基于下面解释的贝叶斯定理：

贝叶斯定理

Renyi 的概率公理检查条件概率，其中事件A和事件B发生的可能性是依赖的或有条件的。 基本条件概率可以写成：

事件 B 发生的概率取决于事件 A。

上述等式是贝叶斯规则的基础，贝叶斯定理的数学表达式表明：

这里，∩表示交集。

贝叶斯规则可以写成：

贝叶斯规则是贝叶斯统计的基础，其中统计模型中特定参数的可用信息与收集的数据进行比较和更新。

背景知识表示为先验分布，然后将其与观察或收集的数据作为似然函数进行比较和研究，以找出后验分布。

这种后验分布用于对未来事件进行预测。

贝叶斯方法的应用取决于以下参数：

1. 定义先验模型和数据模型
2. 做出相关推论
3. 审查和简化模型

什么是贝叶斯神经网络？

贝叶斯神经网络 (BNN) 是您在使用统计方法扩展标准网络并更改后验推理以跟踪过度拟合时创建的网络。 由于它是贝叶斯方法，因此存在与神经网络参数相关的概率分布。

它们用于解决没有可用数据自由流动的复杂问题。 贝叶斯神经网络有助于控制分子生物学和医学诊断等领域的过度拟合。

人们可以考虑问题答案的整个分布，而不仅仅是使用贝叶斯神经网络的一种可能性。 它们帮助您确定模型选择/比较并解决涉及正则化的问题。

贝叶斯统计提供了数学工具来合理化和更新有关新数据或科学证据的主观知识。 与频繁统计方法不同，它的功能基于概率取决于在相同条件下重复事件的频率的假设。

简而言之，贝叶斯技术是个人假设和观点的延伸。 贝叶斯模型使其更有效的关键方面是它理解个人根据他们收到的信息类型的不同意见。

然而，随着新证据和数据的出现，个体有一个收敛点，即贝叶斯推理。 这种合理的更新是贝叶斯统计的特点，使其在分析问题上更加有效。

这里，当事件发生没有希望时应用概率 0，当确定事件会发生时应用概率 1。 介于 0 和 1 之间的概率为其他潜在结果提供了空间。

现在应用贝叶斯规则来实现贝叶斯推理，从而从模型中获得更好的推理。

您如何应用贝叶斯规则来获得贝叶斯推理？

考虑方程：

P(θ|D) = P(D|θ.)P(θ) / P(D)

P(θ) 表示先验分布，

P(θ|D) 表示后验信念，

P(D) 代表证据，

P(D|θ) 表示可能性。

贝叶斯推理的主要目标是提供一种合理且数学上准确的方法，用于将信念与证据混合以获得更新的后验信念。 当生成新数据时，后验信念可以用作先验信念。 因此，贝叶斯推理有助于在贝叶斯规则的帮助下不断更新信念。

考虑相同的抛硬币示例，贝叶斯模型通过新的抛硬币将过程从之前的信念更新为后置信念。 贝叶斯方法给出以下概率。

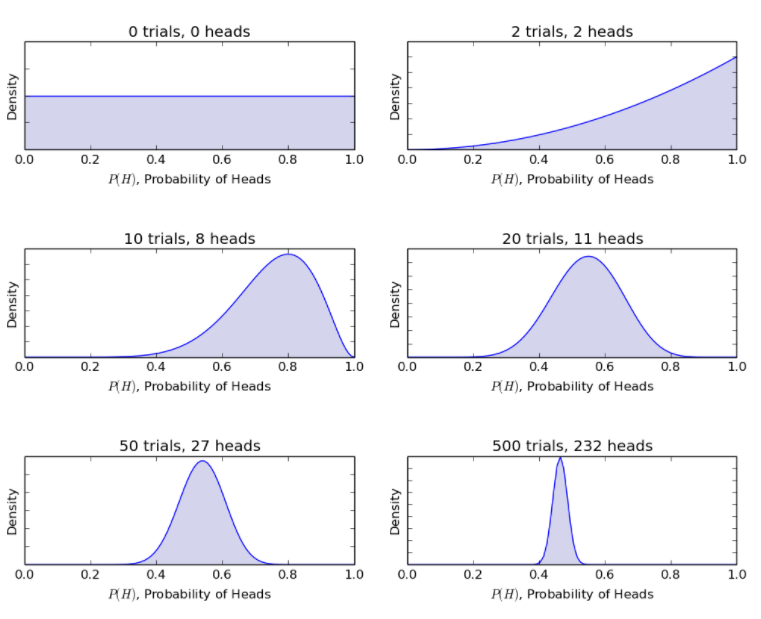
资源

因此，贝叶斯模型允许将具有有限信息的不确定场景合理化为具有大量数据的更明确的场景。

贝叶斯模型和频率模型之间的显着差异

频繁统计

贝叶斯统计

目标被认为是一个点估计，而 CI

目标被认为是后验分布

该程序从观察开始

该过程从先验分布开始

每当进行新的观察时，频率论方法都会重新计算现有模型。

每当进行新的观察时，后验分布（意识形态/假设）都会更新

示例：均值估计、t 检验和 ANOVA。

示例：估计高密度区间的均值和重叠的后验分布。

贝叶斯统计的优势

• 它提供了一种有机而简单的方法，将预先设想的信息与具有科学证据的坚实框架相结合。 有关参数的过去信息可用于形成先验分布以供将来调查。 推论符合贝叶斯定理。
• 贝叶斯模型的推论在逻辑上和数学上是准确的，而不是粗略的假设。 无论样本大小如何，准确度都保持不变。
• 贝叶斯统计遵循似然原理。 当两个不同的样本对于一个信念 θ 有一个共同的似然函数时，关于这个信念的所有推论应该是相似的。 经典统计技术不遵循似然原则。
• 贝叶斯分析的解决方案很容易解释。
• 它为分层模型和不完整数据问题等各种模型提供了有利的平台。 借助其他数值技术，可以虚拟跟踪所有参数模型的计算。

贝叶斯模型在历史上的成功应用

贝叶斯方法在二战期间有很多成功的应用。 下面列出了其中的一些：

• 俄罗斯统计学家Andrey Kolmogorov成​​功地使用贝叶斯方法提高了俄罗斯火炮的效率。
• 贝叶斯模型被用来破解德国 U 型船的密码。
• 出生于法国的美国数学家伯纳德·考普曼（Bernard Koopman）借助贝叶斯模型拦截无线电传输，帮助盟军确定了德国 U 型船的位置。

如果您想了解有关贝叶斯统计的更多信息，请参阅 upGrad 的机器学习和云高级认证，通过现实生活中的行业项目和案例研究来了解基本概念。 为期 12 个月的课程由 IIT Madras 提供，支持自主学习。

联系我们了解更多详情。