贝叶斯网络示例 [带图形表示]

介绍

在统计学中，概率模型用于定义变量之间的关系，并可用于计算每个变量的概率。 在许多问题中，存在大量变量。 在这种情况下，完全条件模型需要大量数据来涵盖概率函数的每一种情况，这可能难以实时计算。 已经有几次尝试简化条件概率计算，例如朴素贝叶斯，但仍然证明它不是有效的，因为它大大减少了几个变量。

唯一的方法是开发一个模型，该模型可以保留随机变量之间的条件依赖关系和其他情况下的条件独立性。 这将我们引向贝叶斯网络的概念。 这些贝叶斯网络帮助我们有效地可视化每个域的概率模型，并以用户友好的图形的形式研究随机变量之间的关系。

从世界顶级大学学习ML 课程。 获得硕士、Executive PGP 或高级证书课程以加快您的职业生涯。

什么是贝叶斯网络？

根据定义，贝叶斯网络是一种概率图形模型，它使用贝叶斯推理进行概率计算。 它用有向无环图 (DAG) 表示一组变量及其条件概率。 它们主要适用于考虑已发生的事件并预测几种可能的已知原因中的任何一种是促成因素的可能性。

资源

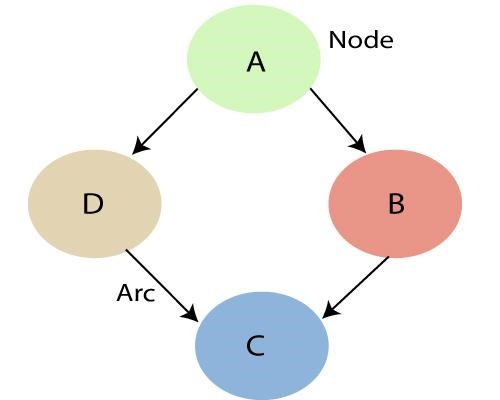
如上所述，通过利用贝叶斯网络指定的关系，我们可以获得具有条件概率的联合概率分布（JPF）。 图中的每个节点代表一个随机变量，弧（或有向箭头）代表节点之间的关系。 它们本质上可以是连续的或离散的。

在上图中，A、B、C 和 D 是 4 个随机变量，由图中网络中给定的节点表示。 对于节点 B，A 是它的父节点，C 是它的子节点。 节点 C 独立于节点 A。

在我们开始实施贝叶斯网络之前，必须了解一些概率基础知识。

局部马尔可夫性质

贝叶斯网络满足称为局部马尔可夫性质的性质。 它指出，给定其父节点，节点有条件地独立于其非后代。 在上面的例子中，P(D|A, B) 等于 P(D|A)，因为 D 独立于它的非后裔 B。这个属性有助于我们简化联合分布。 局部马尔可夫属性将我们引向马尔可夫随机场的概念，它是围绕一个变量的随机场，据说它遵循马尔可夫属性。

条件概率

在数学中，事件 A 的条件概率是在另一个事件 B 已经发生的情况下，事件 A 发生的概率。 简单来说，p(A | B) 是在给定事件 B 发生的情况下，事件 A 发生的概率。 但是，在 A 和 B 之间有两种事件可能性。它们可能是依赖事件，也可能是独立事件。 根据它们的类型，有两种不同的方法来计算条件概率。

• 给定 A 和 B 是相关事件，条件概率计算为 P (A| B) = P (A 和 B) / P (B)
• 如果 A 和 B 是独立事件，则条件概率的表达式为： P(A| B) = P (A)

联合概率分布

在我们进入贝叶斯网络的例子之前，让我们了解联合概率分布的概念。 考虑 3 个变量 a1、a2 和 a3。 根据定义，a1、a2 和 a3 的所有不同可能组合的概率称为其联合概率分布。

如果 P[a1,a2,a3,…..,an] 是从 a1 到 an 的以下变量的 JPD，那么有几种方法可以计算联合概率分布作为各种项的组合，例如，

P[a1,a2, a3,….., an] = P[a1 | a2, a3,….., an] * P[a2, a3,….., an]

= P[a1 | a2, a3,….., 一个] * P[a2 | a3,….., an]….P[an-1|an] * P[an]

推广上述方程，我们可以将联合概率分布写为，

P(X i |X i-1 ,………, X n ) = P(X i |Parents(X i ))

贝叶斯网络示例

现在让我们借助一个简单的例子来了解贝叶斯网络的机制及其优势。 在这个例子中，让我们假设我们的任务是为学生刚刚参加的考试的分数 ( m ) 建模。 从下面给定的贝叶斯网络图中，我们看到标记取决于其他两个变量。 他们是，

• 考试等级（ e ）——这个离散变量表示考试的难度，有两个值（0 表示容易，1 表示困难）
• 智商水平 ( i ) – 这代表学生的智商水平，并且在本质上也是离散的，具有两个值（0 表示低，1 表示高）

此外，学生的智商水平也将我们引向另一个变量，即学生的 Aptitude Score ( s )。 现在，有了学生的分数，他就可以确保进入特定的大学。 下面还给出了被大学录取 ( a ) 的概率分布。

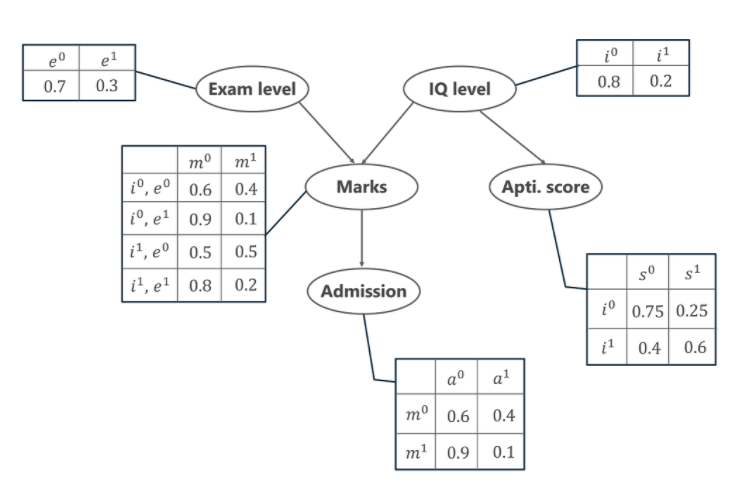
在上图中，我们看到几个表格表示给定 5 个变量的概率分布值。 这些表称为条件概率表或 CPT。 下面给出了 CPT 的一些属性——

• 每行中 CPT 值的总和必须等于 1，因为特定变量的所有可能情况都是详尽无遗的（代表所有可能性）。
• 如果一个本质上是布尔变量的变量有 k 个布尔值，那么在 CPT 中它有 2K 个概率值。

回到我们的问题，让我们首先列出上表中发生的所有可能事件。

1. 考试等级 (e)
2. 智商水平 (i)
3. 能力倾向得分（s）
4. 标记（米）
5. 入场（一）

这五个变量以贝叶斯网络格式的有向无环图 (DAG) 的形式及其条件概率表表示。 现在，要计算 5 个变量的联合概率分布，公式由下式给出，

P[a, m, i, e, s]= P(a | m) 。 P(m | i, e) 。 （一）。 P(e) 。 P(s | i)

由上式可知，

• P(a | m) 表示学生根据他在考试中获得的分数获得录取的条件概率。
• P(m | i, e) 表示根据学生的 IQ 水平和考试级别的难度，学生将获得的分数。
• P(i) 和 P(e) 代表 IQ Level 和 Exam Level 的概率。
• P(s | i) 是给定学生 IQ 水平的学生能力倾向分数的条件概率。

通过计算以下概率，我们可以找到整个贝叶斯网络的联合概率分布。

联合概率分布的计算

现在让我们计算两种情况的 JPD。

案例1：计算尽管考试难度很大，但智商水平低、能力倾向分数低的学生通过考试并获得大学录取的概率。

从上面的文字问题陈述中，联合概率分布可以写成如下，

P[a=1, m=1, i=0, e=1, s=0]

从上面的条件概率表中，给定条件的值被输入公式并计算如下。

P[a=1, m=1, i=0, e=0, s=0] = P(a=1 | m=1) 。 P(m=1 | i=0, e=1) 。 P(i=0) 。 P(e=1) 。 P(s=0 | i=0)

= 0.1 * 0.1 * 0.8 * 0.3 * 0.75

= 0.0018

案例 2：在另一种情况下，计算学生具有高 IQ 水平和 Aptitude Score 的概率，考试很容易但未能通过并且不能确保被大学录取。

JPD 的公式由下式给出

P[a=0, m=0, i=1, e=0, s=1]

因此，

P[a=0, m=0, i=1, e=0, s=1]= P(a=0 | m=0) 。 P(m=0 | i=1, e=0) 。 P(i=1) 。 P(e=0) 。 P(s=1 | i=1)

= 0.6 * 0.5 * 0.2 * 0.7 * 0.6

= 0.0252

因此，通过这种方式，我们可以利用贝叶斯网络和概率表来计算各种可能发生的事件的概率。

另请阅读：机器学习项目的想法和主题

结论

贝叶斯网络在垃圾邮件过滤、语义搜索、信息检索等方面有无数的应用。 例如，对于给定的症状，我们可以预测疾病与其他几个导致疾病的因素一起发生的概率。 因此，本文介绍了贝叶斯网络的概念，并通过一个实际示例对其实现进行了介绍。

如果您想掌握机器学习和人工智能，请通过 IIIT-B 和利物浦约翰摩尔斯大学的机器学习和人工智能高级课程提升您的职业生涯。