机器学习中的贝叶斯定理:简介、如何应用和示例
已发表: 2021-02-04目录
简介:什么是贝叶斯定理?
贝叶斯定理以英国数学家托马斯·贝叶斯的名字命名,他在决策理论(涉及概率的数学领域)广泛工作。 贝叶斯定理也广泛用于机器学习,它是一种简单、有效的方法来准确地预测类别。 计算条件概率的贝叶斯方法用于涉及分类任务的机器学习应用程序。
贝叶斯定理的简化版本,称为朴素贝叶斯分类,用于减少计算时间和成本。 在本文中,我们将带您了解这些概念并讨论贝叶斯定理在机器学习中的应用。
加入来自世界顶级大学的在线机器学习课程——硕士、高级管理人员研究生课程和 ML 和 AI 高级证书课程,以加快您的职业生涯。
为什么在机器学习中使用贝叶斯定理?
贝叶斯定理是一种确定条件概率的方法,即在另一个事件已经发生的情况下,一个事件发生的概率。 因为条件概率包括额外的条件——换句话说,更多的数据——它可以促成更准确的结果。
因此,条件概率是确定机器学习中准确预测和概率的必要条件。 鉴于该领域在各个领域变得越来越普遍,了解贝叶斯定理等算法和方法在机器学习中的作用非常重要。
在我们进入定理本身之前,让我们通过一个例子来理解一些术语。 假设书店经理有关于他的顾客年龄和收入的信息。 他想知道图书销售如何分布在三个年龄段的客户中:青年(18-35 岁)、中年(35-60 岁)和老年人(60 岁以上)。

让我们将我们的数据称为 X。在贝叶斯术语中,X 称为证据。 我们有一些假设 H,其中我们有一些属于某个 C 类的 X。
我们的目标是确定给定 X 的假设 H 的条件概率,即 P(H | X)。
简单来说,通过确定 P(H | X),我们得到 X 属于 C 类的概率,给定 X。X 具有年龄和收入的属性——例如,26 岁,收入为 2000 美元。 H 是我们的假设,即客户会购买这本书。
密切关注以下四个术语:
- 证据——如前所述,P(X) 被称为证据。 在这种情况下,这只是客户年满 26 岁并赚取 2000 美元的概率。
- 先验概率——P(H),称为先验概率,是我们假设的简单概率——即客户将购买一本书。 基于年龄和收入的任何额外输入都不会提供此概率。 由于计算是用较少的信息完成的,因此结果不太准确。
- 后验概率– P(H | X) 被称为后验概率。 这里,P(H | X) 是给定 X 的顾客购买一本书 (H) 的概率(他 26 岁,收入 2000 美元)。
- 似然性——P(X | H) 是似然概率。 在这种情况下,假设我们知道客户会购买这本书,似然概率是客户年龄为 26 岁且收入为 2000 美元的概率。
鉴于这些,贝叶斯定理指出:
P(H | X) = [ P(X | H) * P(H) ] / P(X)
注意定理中上述四个项的出现——后验概率、似然概率、先验概率和证据。
阅读:朴素贝叶斯解释
如何在机器学习中应用贝叶斯定理
朴素贝叶斯分类器是贝叶斯定理的简化版本,被用作分类算法,以准确和快速地将数据分类为各种类别。
让我们看看如何将朴素贝叶斯分类器用作分类算法。
- 考虑一个一般的例子:X 是一个由“n”个属性组成的向量,即 X = {x1, x2, x3, ..., xn}。
- 假设我们有“m”类 {C1, C2, ..., Cm}。 我们的分类器必须预测 X 属于某个类别。 提供最高后验概率的类将被选为最佳类。 所以在数学上,分类器将预测类别 Ci iff P(Ci | X) > P(Cj | X)。 应用贝叶斯定理:
P(Ci | X) = [ P(X | Ci) * P(Ci) ] / P(X)
- P(X) 与条件无关,对于每个类都是常数。 所以为了最大化 P(Ci | X),我们必须最大化 [P(X | Ci) * P(Ci)]。 考虑到每个类别的可能性相同,我们有 P(C1) = P(C2) = P(C3) ... = P(Cn)。 所以最终,我们只需要最大化 P(X | Ci)。
- 由于典型的大型数据集可能具有多个属性,因此对每个属性执行 P(X | Ci) 操作的计算成本很高。 这就是类条件独立性的用武之地,以简化问题并降低计算成本。 通过类条件独立性,我们的意思是我们认为属性的值有条件地相互独立。 这就是朴素贝叶斯分类。
P(Xi | C) = P(x1 | C) * P(x2 | C) *… * P(xn | C)
现在很容易计算较小的概率。 这里需要注意一件重要的事情:由于 xk 属于每个属性,我们还需要检查我们正在处理的属性是categorical还是Continuous 。
- 如果我们有一个分类属性,事情就更简单了。 我们可以只计算由属性 k 的值 xk 组成的类 Ci 的实例数,然后将其除以类 Ci 的实例数。
- 如果我们有一个连续属性,考虑到我们有一个正态分布函数,我们应用以下公式,均值 ? 和标准差?:
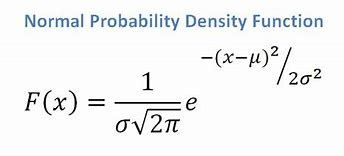

资源
最终,我们将有 P(x | Ci) = F(xk, ?k, ?k)。
- 现在,我们有了对每个类 Ci 使用贝叶斯定理所需的所有值。 我们预测的类将是实现最高概率 P(X | Ci) * P(Ci) 的类。
示例:对书店的客户进行预测性分类
我们有来自书店的以下数据集:
| 年龄 | 收入 | 学生 | 信用评级 | 买书 |
| 青年 | 高的 | 不 | 公平的 | 不 |
| 青年 | 高的 | 不 | 优秀 | 不 |
| 中年 | 高的 | 不 | 公平的 | 是的 |
| 高级的 | 中等的 | 不 | 公平的 | 是的 |
| 高级的 | 低的 | 是的 | 公平的 | 是的 |
| 高级的 | 低的 | 是的 | 优秀 | 不 |
| 中年 | 低的 | 是的 | 优秀 | 是的 |
| 青年 | 中等的 | 不 | 公平的 | 不 |
| 青年 | 低的 | 是的 | 公平的 | 是的 |
| 高级的 | 中等的 | 是的 | 公平的 | 是的 |
| 青年 | 中等的 | 是的 | 优秀 | 是的 |
| 中年 | 中等的 | 不 | 优秀 | 是的 |
| 中年 | 高的 | 是的 | 公平的 | 是的 |
| 高级的 | 中等的 | 不 | 优秀 | 不 |
我们有年龄、收入、学生和信用等级等属性。 我们的类 buys_book 有两个结果:Yes 或 No。
我们的目标是根据以下属性进行分类:
X = {年龄 = 青年,学生 = 是,收入 = 中等,credit_rating = 一般}。
如前所述,为了最大化 P(Ci | X),我们需要在 i = 1 和 i = 2 时最大化 [ P(X | Ci) * P(Ci) ]。
因此,P(buys_book = yes) = 9/14 = 0.643
P(buys_book = no) = 5/14 = 0.357
P(年龄=青年|购买书=是)= 2/9 = 0.222
P(年龄 = 青年 | 购买书 = 否) =3/5 = 0.600
P(收入 = 中等 | 购买书 = 是)= 4/9 = 0.444
P(收入 = 中等 | 购买书 = 否)= 2/5 = 0.400
P(学生 = 是 | 购买书 = 是)= 6/9 = 0.667
P(学生 = 是 | 购买书 = 否)= 1/5 = 0.200
P(credit_rating = fair | buys_book = yes) = 6/9 = 0.667
P(credit_rating = fair | buys_book = no) = 2/5 = 0.400
使用上面计算的概率,我们有
P(X | buys_book = 是) = 0.222 x 0.444 x 0.667 x 0.667 = 0.044
相似地,
P(X | buys_book = no) = 0.600 x 0.400 x 0.200 x 0.400 = 0.019
Ci 哪个类提供最大 P(X|Ci)*P(Ci)? 我们计算:
P(X | buys_book = 是)* P(buys_book = 是) = 0.044 x 0.643 = 0.028
P(X | buys_book = no)* P(buys_book = no) = 0.019 x 0.357 = 0.007

比较以上两者,由于 0.028 > 0.007,朴素贝叶斯分类器预测具有上述属性的客户会购买一本书。
结帐:机器学习项目的想法和主题
贝叶斯分类器是一个好方法吗?
机器学习中基于贝叶斯定理的算法提供了与其他算法相当的结果,贝叶斯分类器通常被认为是简单的高精度方法。 但是,应注意贝叶斯分类器特别适用于类条件独立性假设有效的情况,而不是适用于所有情况。 另一个实际问题是获取所有概率数据可能并不总是可行的。
结论
贝叶斯定理在机器学习中有许多应用,特别是在基于分类的问题中。 在机器学习中应用这一系列算法需要熟悉诸如先验概率和后验概率等术语。 在本文中,我们讨论了贝叶斯定理的基础知识,它在机器学习问题中的应用,并通过一个分类示例进行了工作。
由于贝叶斯定理是机器学习中基于分类的算法的重要组成部分,因此您可以了解有关upGrad 机器学习和 NLP 高级证书课程的更多信息。 本课程的设计考虑到对机器学习感兴趣的各种学生,提供 1-1 指导等等。
为什么我们在机器学习中使用贝叶斯定理?
贝叶斯定理是一种计算条件概率的方法,即如果另一个事件之前发生过,则另一个事件发生的可能性。 条件概率可以通过包含额外条件(换句话说,更多数据)来产生更准确的结果。 为了在机器学习中获得正确的估计和概率,需要条件概率。 鉴于该领域在广泛领域的日益普及,理解贝叶斯定理等算法和方法在机器学习中的重要性至关重要。
贝叶斯分类器是一个不错的选择吗?
在机器学习中,基于贝叶斯定理的算法产生的结果与其他方法相当,贝叶斯分类器被广泛认为是简单的高精度方法。 但是,重要的是要记住,贝叶斯分类器最好在类条件独立的条件正确时使用,而不是在所有情况下。 另一个考虑是获得所有可能性数据可能并不总是可能的。
贝叶斯定理如何实际应用?
贝叶斯定理根据与之相关或可能相关的新证据来计算发生的可能性。 该方法还可用于查看假设的新信息如何影响事件的可能性,假设新信息是真实的。 以从一副 52 张牌中选出的一张牌为例。 这张牌成为国王的概率是 4 除以 52,即 1/13,或大约 7.69%。 请记住,套牌包含四张国王。 假设显示所选卡是面卡。 因为一副牌中有 12 张面牌,所以选择的牌是 K 的概率是 4 除以 12,即大约 33.3%。
