用示例解释贝叶斯定理 – 完整指南

介绍

什么是贝叶斯定理？

贝叶斯定理用于计算直觉经常失败的条件概率。 尽管在概率中被广泛使用，但该定理也被应用于机器学习领域。 它在机器学习中的使用包括将模型拟合到训练数据集和开发分类模型。

什么是条件概率？

条件概率通常定义为在给定另一事件发生的情况下一个事件的概率。

• 如果 A 和 B 是两个事件，则条件概率 me 被指定为 P(A given B) 或 P(A|B)。
• 条件概率可以由联合概率(A | B) = P(A, B) / P(B) 计算

• 条件概率不对称； 例如 P(A | B) != P(B | A)

计算条件概率的其他方法包括使用其他条件概率，即

P(A|B) = P(B|A) * P(A) / P(B)

也使用反向

P(B|A) = P(A|B) * P(B) / P(A)

当难以计算联合概率时，这种计算方式很有用。 否则，当反向条件概率可用时，通过它进行计算变得容易。

这种条件概率的替代计算称为贝叶斯规则或贝叶斯定理。 它以第一个描述它的人的名字命名，“托马斯·贝叶斯牧师”。

贝叶斯定理公式

贝叶斯定理是一种在联合概率不可用时计算条件概率的方法。 有时，不能直接访问分母。 在这种情况下，另一种计算方法如下：

P(B) = P(B|A) * P(A) + P(B|非 A) * P(非 A)

这是贝叶斯定理的公式，它显示了 P(B) 的替代计算。

P(A|B) = P(B|A) * P(A) / P(B|A) * P(A) + P(B|非 A) * P(非 A)

上面的公式可以用分母括起来的括号来描述

P(A|B) = P(B|A) * P(A) / (P(B|A) * P(A) + P(B|非 A) * P(非 A))

此外，如果我们有 P(A)，那么 P(not A) 可以计算为

P(不是 A) = 1 – P(A)

类似地，如果我们有 P(not B|not A)，那么 P(B|not A) 可以计算为

P(B|非 A) = 1 – P(非 B|非 A)

条件概率的贝叶斯定理

贝叶斯定理由几个术语组成，其名称是根据其在方程中的应用上下文给出的。

后验概率是指P(A|B)的结果，先验概率是指P(A)的结果。

• P(A|B)：后验概率。
• P(A)：先验概率。

类似地，P(B|A) 和 P(B) 被称为可能性和证据。

• P(B|A)：可能性。
• P(B)：证据。

因此，条件概率的贝叶斯定理可以重新表述为：

后验=可能性*先验/证据

如果我们必须在有烟的情况下计算发生火灾的概率，那么将使用以下等式：

P(火|烟) = P(烟|火) * P(火) / P(烟)

其中，P(Fire) 是先验，P(Smoke|Fire) 是可能性，P(Smoke) 是证据。

贝叶斯定理的说明

描述了贝叶斯定理示例以说明贝叶斯定理在问题中的使用。

问题

存在三个标记为 A、B 和 C 的框。 盒子的详细信息是：

• 盒子 A 包含 2 个红球和 3 个黑球
• 盒子 B 包含 3 个红球和 1 个黑球
• 盒子 C 包含 1 个红球和 4 个黑球

所有三个盒子都是相同的，被拾取的概率相等。 因此，从盒子 A 中捡到红球的概率是多少？

解决方案

令 E 表示捡起红球的事件，而 A、B 和 C 表示从各自的盒子中捡起球。 因此，条件概率将是需要计算的 P(A|E)。

现有概率 P(A) = P(B) = P (C) = 1 / 3，因为所有盒子被选中的概率相等。

P(E|A) = 盒子 A 中的红球数 / 盒子 A 中的球总数 = 2 / 5

同样，P(E|B) = 3 / 4 和 P(E|C) = 1 / 5

那么证据 P(E) = P(E|A)*P(A) + P(E|B)*P(B) + P(E|C)*P(C)

= (2/5) * (1/3) + (3/4) * (1/3) + (1/5) * (1/3) = 0.45

因此，P(A|E) = P(E|A) * P(A) / P(E) = (2/5) * (1/3) / 0.45 = 0.296

贝叶斯定理的例子

贝叶斯定理给出了“事件”与“测试”的给定信息的概率。

• “事件”和“测试”是有区别的。 例如，有一项针对肝病的测试，这与实际患有肝病不同，即一个事件。
• 罕见事件可能具有更高的误报率。

示例 1

如果患者酗酒，患肝病的概率是多少？

在这里，“酗酒”是肝病的“测试”（试金石的类型）。

• A是事件，即“患者患有肝病”。

根据该诊所早期的记录，它指出进入诊所的患者中有10％患有肝病。

因此，P(A)=0.10

• B 是“患者是酒鬼”的试金石。

该诊所早前的记录显示，进入诊所的患者中有 5% 是酗酒者。

因此，P(B)=0.05

• 此外，在被诊断患有肝病的患者中，有 7% 是酗酒者。 这定义了 B|A：考虑到患者患有肝病，患者酗酒的概率为 7%。

根据贝叶斯定理公式，

P(A|B) = (0.07 * 0.1)/0.05 = 0.14

因此，对于酗酒的患者，患肝病的几率为 0.14 (14%)。

示例 2

• 危险火灾很少见（1%）
• 但由于烧烤，烟雾相当普遍（10%），
• 90% 的危险火灾会产生烟雾

有烟雾时发生危险火灾的概率是多少？

计算

P(火|烟) =P(火) P(烟|火)/P(烟)

= 1% x 90%/10%

= 9%

示例 3

白天下雨的可能性有多大？ 其中，Rain 表示白天下雨，Cloud 表示多云的早晨。

给定 Cloud 下雨的机会写成 P(Rain|Cloud)

P(雨|云) = P(雨) P(云|雨)/P(云)

P(Rain) 是下雨的概率 = 10%

P(Cloud|Rain) 是云的概率，假设下雨发生 = 50%

P(Cloud) 是 Cloud 的概率 = 40%

P（雨|云）= 0.1 x 0.5/0.4 = .125

因此，有 12.5% 的几率下雨。

应用

贝叶斯定理的几种应用存在于现实世界中。 该定理的几个主要应用是：

1. 建模假设

贝叶斯定理在应用机器学习中得到了广泛的应用，并建立了数据和模型之间的关系。 应用机器学习使用对给定数据集的不同假设进行测试和分析的过程。

为了描述数据和模型之间的关系，贝叶斯定理提供了一个概率模型。

P(h|D) = P(D|h) * P(h) / P(D)

在哪里，

P(h|D)：假设的后验概率

P(h)：假设的先验概率。

P(D) 的增加会降低 P(h|D)。 相反，如果 P(h) 和给定假设观察数据的概率增加，则 P(h|D) 的概率增加。

2.贝叶斯分类定理

分类方法涉及给定数据的标记。 它可以定义为给定数据样本的类标签的条件概率的计算。

P(类|数据) = (P(数据|类) * P(类)) / P(数据)

其中 P(class|data) 是给定数据的类别概率。

可以对每一类进行计算。 可以将具有最大概率的类分配给输入数据。

在样本数量较少的情况下，条件概率的计算是不可行的。 因此，贝叶斯定理的直接应用是不可行的。 分类模型的解决方案在于简化计算。

• 朴素贝叶斯分类器

贝叶斯定理认为输入变量依赖于其他变量，导致计算复杂。 因此，假设被删除，每个输入变量都被视为一个自变量。 结果，模型从依赖条件概率模型变为独立条件概率模型。 它最终降低了复杂性。

贝叶斯定理的这种简化称为朴素贝叶斯。 它广泛用于分类和预测模型。

• 贝叶斯最优分类器

这是一种概率模型，涉及在给定训练数据集的情况下预测新示例。 贝叶斯最优分类器的一个例子是“给定训练数据，新实例最可能的分类是什么？”

在给定训练数据的情况下计算新实例的条件概率可以通过以下等式完成

P(vj | D) = sum {h in H} P(vj | hi) * P(hi | D)

其中 vj 是要分类的新实例，

H 是用于对实例进行分类的假设集，

hi 是一个给定的假设，

P(vj | hi) 是给定假设 hi 的 vi 的后验概率，并且

P(hi | D) 是给定数据 D 的假设 hi 的后验概率。

3. 贝叶斯定理在机器学习中的应用

贝叶斯定理在机器学习中最常见的应用是分类问题的发展。 其他应用而不是分类包括优化和临时模型。

• 贝叶斯优化

找到导致给定目标函数的最小或最大成本的输入始终是一项具有挑战性的任务。 贝叶斯优化基于贝叶斯定理，为搜索全局优化问题提供了一个方面。 该方法包括概率模型（代理函数）的构建、通过采集函数进行搜索以及选择用于评估真实目标函数的候选样本。

在应用机器学习中，贝叶斯优化用于调整性​​能良好的模型的超参数。

• 贝叶斯信念网络

变量之间的关系可以通过使用概率模型来定义。 它们也用于概率的计算。 由于大量数据，完全条件概率模型可能无法计算概率。 朴素贝叶斯简化了计算方法。 还存在另一种方法，其中基于随机变量之间的已知条件依赖性和其他情况下的条件独立性开发模型。 贝叶斯网络通过有向边的概率图模型展示了这种依赖性和独立性。 已知的条件相关性显示为有向边，缺失的连接表示模型中的条件独立性。

4.贝叶斯垃圾邮件过滤

垃圾邮件过滤是贝叶斯定理的另一个应用。 存在两个事件：

• 事件 A：邮件是垃圾邮件。
• 测试 X：消息包含某些单词 (X)

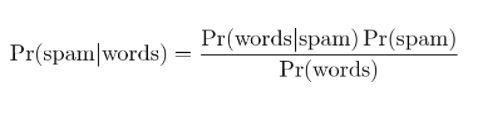
通过应用贝叶斯定理，可以根据“测试结果”来预测邮件是否为垃圾邮件。 分析邮件中的单词可以计算成为垃圾邮件的机会。 通过使用重复消息训练过滤器，它更新了消息中包含某些单词的概率是垃圾邮件的事实。

贝叶斯定理的应用举例

催化剂生产商生产一种用于测试某种电催化剂 (EC) 缺陷的装置。 这家催化剂生产商声称，如果 EC 有缺陷，则该测试的可靠性为 97%，如果无缺陷，则该测试的可靠性为 99%。 但是，预计 4% 的上述 EC 在交付时会出现缺陷。 应用贝叶斯规则来确定设备的真实可靠性。 基本事件集是

A：EC有缺陷； A'：EC完美无瑕； B：EC检测有缺陷； B'：EC经测试无瑕疵。

概率是

B/A：EC 是（已知）有缺陷的，并且测试有缺陷，P(B/A) = 0.97，

B'/A：EC（已知）有缺陷，但测试无缺陷，P(B'/A)=1-P(B/A)=0.03，

B/A'：EC（已知）有缺陷，但经测试有缺陷，P(B/A') = 1- P(B'/A')=0.01

B'/A: = EC （已知）完美无瑕，经测试完美无瑕 P(B'/A') = 0.99

贝叶斯定理计算的概率为：

计算的概率表明，拒绝无缺陷 EC 的可能性很高（约 20%），而识别有缺陷的 EC 的可能性很低（约 80%）。

结论

贝叶斯定理最显着的特点之一是，从几个概率比中，可以获得大量的信息。 通过似然法，先验事件的概率可以转换为后验概率。 贝叶斯定理的方法可以应用于统计、认识论和归纳逻辑领域。

如果您有兴趣了解有关贝叶斯定理、人工智能和机器学习的更多信息，请查看 IIIT-B 和 upGrad 的机器学习和人工智能执行 PG 计划，该计划专为工作专业人士设计，提供 450 多个小时的严格培训，30 多个案例学习和作业、IIIT-B 校友身份、5 个以上实用的实践顶点项目和顶级公司的工作协助。