Veri Madenciliğinde Karar Ağacı Nedir? Türler, Gerçek Dünya Örnekleri ve Uygulamaları

Veri Madenciliğine Giriş

Veriler genellikle, faydalı bilgilere dönüştürülmesi için etkin bir şekilde işlenmesi gereken ham veriler olarak bulunur. Sonuçların tahmini genellikle verilerdeki kalıpları, anormallikleri veya korelasyonları bulma sürecine dayanır. Süreç “veritabanlarında bilgi keşfi” olarak adlandırıldı.

“Veri madenciliği” terimi ancak 1990'larda ortaya çıktı. Veri madenciliği üç disiplin üzerine kurulmuştur: istatistik, yapay zeka ve makine öğrenimi. Otomatik veri madenciliği, analiz sürecini sıkıcı bir yaklaşımdan daha hızlı bir yaklaşıma kaydırdı. Veri madenciliği, kullanıcının

• • Tüm gürültülü ve kaotik verileri kaldırın
  • İlgili verileri anlayın ve faydalı bilgilerin tahmini için kullanın.
  • Bilgilendirilmiş kararları tahmin etme süreci hızlandırılır .

Veri madenciliği, kategorizasyon gerektiren gizli bilgi kalıplarını belirleme süreci olarak da ifade edilebilir. Ancak o zaman veriler faydalı verilere dönüştürülebilir. Yararlı veriler bir veri ambarına, veri madenciliği algoritmalarına, karar verme için veri analizine beslenebilir.

Veri madenciliğinde karar ağacı

Bir tür veri madenciliği tekniği olan veri madenciliğinde Karar ağacı, verilerin sınıflandırılması için bir model oluşturur. Modeller ağaç yapısı biçiminde inşa edilmiştir ve bu nedenle denetimli öğrenme biçimine aittir. Sınıflandırma modellerinin dışında, karar verme sürecine yardımcı olan sınıf etiketlerini veya değerleri tahmin etmek için regresyon modelleri oluşturmak için karar ağaçları kullanılır. Cinsiyet, yaş vb. gibi hem sayısal hem de kategorik veriler bir karar ağacı tarafından kullanılabilir.

Karar ağacının yapısı

Bir karar ağacının yapısı bir kök düğüm, dallar ve yaprak düğümlerden oluşur. Dallanmış düğümler bir ağacın sonuçlarıdır ve iç düğümler bir öznitelik üzerindeki testi temsil eder. Yaprak düğümleri bir sınıf etiketini temsil eder.

Karar ağacının çalışması

1. Bir karar ağacı, hem gizli hem de sürekli değişkenler için denetimli öğrenme yaklaşımı altında çalışır. Veri kümesi, veri kümesinin en önemli özniteliği temelinde alt kümelere bölünür. Özniteliğin tanımlanması ve bölünmesi algoritmalar aracılığıyla yapılır.

2. Karar ağacının yapısı, önemli tahmin düğümü olan kök düğümden oluşur. Ağacın alt düğümleri olan karar düğümlerinden bölme işlemi gerçekleşir. Daha fazla bölünmeyen düğümler, yaprak veya uç düğümler olarak adlandırılır.

3. Veri seti, yukarıdan aşağıya bir yaklaşımla homojen ve örtüşmeyen bölgelere ayrılmıştır. Üst katman, gözlemleri tek bir yerde sağlar ve daha sonra dallara ayrılır. Süreç, gelecekteki düğümlerden ziyade yalnızca mevcut düğüme odaklandığı için “Açgözlü Yaklaşım” olarak adlandırılır.

4. Durdurma kriterine ulaşılıncaya kadar karar ağacı çalışmaya devam edecektir.

5. Bir karar ağacının oluşturulmasıyla çok fazla gürültü ve aykırı değer üretilir. Bu aykırı değerleri ve gürültülü verileri ortadan kaldırmak için “Ağaç budama” yöntemi uygulanır. Dolayısıyla modelin doğruluğu artmaktadır.

6. Bir modelin doğruluğu, test demetleri ve sınıf etiketlerinden oluşan bir test seti üzerinde kontrol edilir. Doğru bir model, model tarafından sınıflandırma test seti gruplarının ve sınıflarının yüzdelerine dayalı olarak tanımlanır.

Şekil 1 : Budanmamış ve budanmış bir ağaç örneği

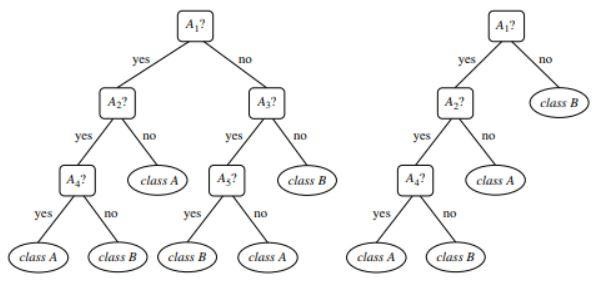
Kaynak

Karar Ağacı Türleri

Karar ağaçları, ağaç benzeri bir yapıya dayalı sınıflandırma ve regresyon için modellerin geliştirilmesine yol açar. Veriler daha küçük alt kümelere bölünür. Karar ağacının sonucu, karar düğümleri ve yaprak düğümleri olan bir ağaçtır. İki tür karar ağacı aşağıda açıklanmıştır:

1. Sınıflandırma

Sınıflandırma, önemli sınıf etiketlerini tanımlayan modellerin oluşturulmasını içerir. Makine öğrenimi ve örüntü tanıma alanlarında uygulanırlar. Sınıflandırma modelleri aracılığıyla makine öğreniminde karar ağaçları, Dolandırıcılık tespiti, tıbbi teşhis vb. yol açar. Bir sınıflandırma modelinin iki aşamalı süreci şunları içerir:

• Öğrenme: Eğitim verilerine dayalı bir sınıflandırma modeli oluşturulur.
• Sınıflandırma: Model doğruluğu kontrol edilir ve ardından yeni verilerin sınıflandırılması için kullanılır. Sınıf etiketleri “evet” veya “hayır” gibi ayrık değerler biçimindedir.

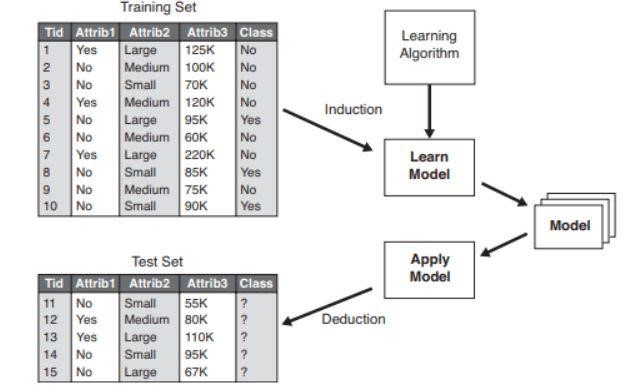
Şekil 2 : Bir sınıflandırma modeli örneği .

Kaynak

2. Regresyon

Regresyon modelleri, verilerin regresyon analizi, yani sayısal niteliklerin tahmini için kullanılır. Bunlara sürekli değerler de denir. Bu nedenle, sınıf etiketlerini tahmin etmek yerine, regresyon modeli sürekli değerleri tahmin eder.

Kullanılan Algoritmaların Listesi

“ID3” olarak bilinen bir karar ağacı algoritması, 1980 yılında J. Ross Quinlan adlı bir makine araştırmacısı tarafından geliştirildi. Bu algoritma, onun tarafından geliştirilen C4.5 gibi diğer algoritmalar tarafından başarılı oldu. Her iki algoritma da açgözlü yaklaşımı uyguladı. C4.5 algoritması geri izleme kullanmaz ve ağaçlar yukarıdan aşağıya özyinelemeli böl ve yönet tarzında oluşturulur. Algoritma, ağaç oluşturuldukça daha küçük alt kümelere ayrılan sınıf etiketleriyle bir eğitim veri kümesi kullandı.

• Başlangıçta üç parametre seçilir: öznitelik listesi, öznitelik seçim yöntemi ve veri bölümü. Eğitim setinin öznitelikleri öznitelik listesinde açıklanmıştır.
• Atıf seçim yöntemi, demetler arasında ayrım için en iyi özniteliğin seçilmesi yöntemini içerir.
• Bir ağaç yapısı, nitelik seçim yöntemine bağlıdır.
• Bir ağacın inşası tek bir düğümle başlar.
• Grupların bölünmesi, bir tanımlama grubunda farklı sınıf etiketleri temsil edildiğinde gerçekleşir. Bu ağacın dal oluşumuna yol açacaktır.
• Bölme yöntemi, veri bölümü için hangi özniteliğin seçilmesi gerektiğini belirler. Bu yönteme göre dallar, testin sonucuna göre bir düğümden büyütülür.
• Bölme ve bölümleme yöntemi özyinelemeli olarak gerçekleştirilir ve sonuçta eğitim veri kümesi demetleri için bir karar ağacı elde edilir.
• Ağaç oluşumu süreci, kalan demetler daha fazla bölünemediği sürece devam eder.
• Algoritmanın karmaşıklığı ile gösterilir

n * |D| * günlük |D|

Burada n, D ve |D| eğitim veri kümesindeki özniteliklerin sayısıdır. tuple sayısıdır.

Kaynak

Şekil 3: Ayrık bir değer bölme

Bir karar ağacında kullanılan algoritmaların listesi:

ID3

Karar ağacı oluşturulurken tüm veri seti S kök düğüm olarak kabul edilir. Daha sonra her öznitelik üzerinde yineleme gerçekleştirilir ve verilerin parçalara bölünmesi. Algoritma, yinelenenlerden önce alınmayan öznitelikleri kontrol eder ve alır. ID3 algoritmasında verileri bölmek zaman alıcıdır ve verilere gereğinden fazla uyduğu için ideal bir algoritma değildir.

C4.5

Veriler örnek olarak sınıflandırıldığından, bir algoritmanın gelişmiş bir şeklidir. ID3'ün aksine hem sürekli hem de ayrık değerler verimli bir şekilde işlenebilir. İstenmeyen dalları ortadan kaldıran budama yöntemi mevcuttur.

ARABA

Algoritma tarafından hem sınıflandırma hem de regresyon görevleri gerçekleştirilebilir. ID3 ve C4.5'ten farklı olarak Gini indeksi dikkate alınarak karar noktaları oluşturulur. Maliyet fonksiyonunu düşürmeyi amaçlayan bölme yöntemi için açgözlü bir algoritma uygulanmaktadır. Sınıflandırma görevlerinde, yaprak düğümlerinin saflığını belirtmek için maliyet fonksiyonu olarak Gini indeksi kullanılır. Regresyon görevlerinde, en iyi tahmini bulmak için maliyet fonksiyonu olarak toplam kare hatası kullanılır.

CHAID

Adından da anlaşılacağı gibi, her tür değişkenle ilgilenen bir süreç olan Ki-kare Otomatik Etkileşim Dedektörü anlamına gelir. Nominal, sıralı veya sürekli değişkenler olabilirler. Regresyon ağaçları F-testini kullanırken, sınıflandırma modelinde Ki-kare testi kullanılır.

MARS

Çok değişkenli uyarlanabilir regresyon eğrileri anlamına gelir. Algoritma, verilerin çoğunlukla doğrusal olmadığı regresyon görevlerinde özel olarak uygulanır.

Açgözlü Özyinelemeli İkili Bölme

İki dal ile sonuçlanan bir ikili bölme yöntemi oluşur. Grupların bölünmesi, bölünmüş maliyet fonksiyonunun hesaplanmasıyla gerçekleştirilir. En düşük maliyet dağılımı seçilir ve süreç, diğer demetlerin maliyet fonksiyonunu hesaplamak için yinelemeli olarak gerçekleştirilir.

Gerçek Dünya Örneği ile Karar Ağacı

Verilen verilerden kredi uygunluk sürecini tahmin edin.

Adım 1: Verilerin yüklenmesi

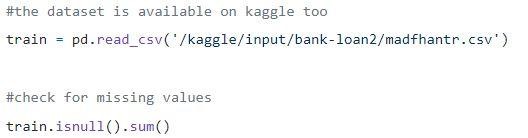
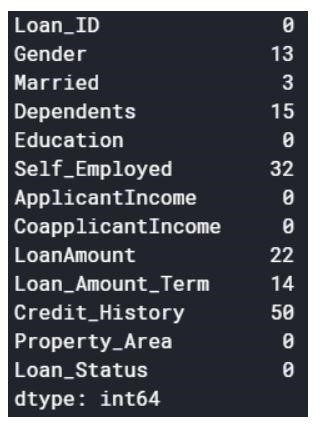
Boş değerler bırakılabilir veya bazı değerlerle doldurulabilir. Orijinal veri kümesinin şekli (614,13) ve boş değerlerin çıkarılmasından sonraki yeni veri kümesi (480,13)'tür.

Adım 2: veri kümesine bir bakış.

Adım 3: Verileri eğitim ve test setlerine bölme.

Adım 4: Modeli oluşturun ve tren setini takın

Görselleştirmeden önce bazı hesaplamalar yapılmalıdır.

Hesaplama 1: toplam veri kümesinin entropisini hesaplayın.

Hesaplama 2: Her sütun için entropiyi ve kazancı bulun.

1. cinsiyet sütunu

• Koşul 1: içinde tüm erkeklerin olduğu veri seti ve sonra,

p = 278, n=116 , p+n=489

Entropi(G=Erkek) = 0.87

• Durum 2: içinde tüm dişiler bulunan veri seti ve sonra,

p = 54 , n = 32 , p+n = 86

Entropi(G=Dişi) = 0.95

• Cinsiyet sütunundaki ortalama bilgi

2. evli sütun

• Durum 1: Evli = Evet(1)

Bu bölünmede tüm veri setini Evli statüsüyle evet

p = 227 , n = 84 , p+n = 311

E(Evli = Evet) = 0.84

• Durum 2: Evli = Hayır(0)

Bu bölünmede tüm veri setini Evli durum no ile böler.

p = 105 , n = 64 , p+n = 169

E(Evli = Hayır) = 0.957

• Evli sütunundaki Ortalama Bilgi (şimdiki değeri)

3. Eğitim sütunu

• Durum 1: Eğitim = Mezun(1)

p = 271 , n = 112 , p+n = 383

E(Eğitim = Mezun) = 0.87

• Durum 2: Eğitim = Mezun Değil(0)

p = 61 , n = 36 , p+n = 97

E(Eğitim = Mezun Değil) = 0.95

• Ortalama Eğitim Bilgileri sütunu= 0.886

Kazanç = 0.01

4) Serbest Meslek Sahibi Sütunu

• Durum 1: Serbest Meslek Sahibi = Evet(1)

p = 43 , n = 23 , p+n = 66

E(Serbest Meslek Sahibi=Evet) = 0.93

• Durum 2: Serbest Meslek Sahibi = Hayır(0)

p = 289 , n = 125 , p+n = 414

E(Serbest Meslek Sahibi=Hayır) = 0.88

• Eğitimde Serbest Meslek Sahibi Olanlar Sütununda Ortalama Bilgi = 0.886

Kazanç = 0.01

5. Kredi Puanı sütunu: sütunun 0 ve 1 değeri vardır.

• Koşul 1: Kredi Puanı = 1

p = 325 , n = 85 , p+n = 410

E(Kredi Puanı = 1) = 0,73

• Koşul 2: Kredi Puanı = 0

p = 63 , n = 7 , p+n = 70

E(Kredi Puanı = 0) = 0,46

• Kredi Puanı sütunundaki Ortalama Bilgi = 0,69

Kazanç = 0,2

Tüm kazanç değerlerini karşılaştırın

Kredi puanı en yüksek kazanıma sahiptir. Bu nedenle, kök düğüm olarak kullanılacaktır.

Adım 5: Karar Ağacını Görselleştirin

Şekil 5: Gini kriterli karar ağacı

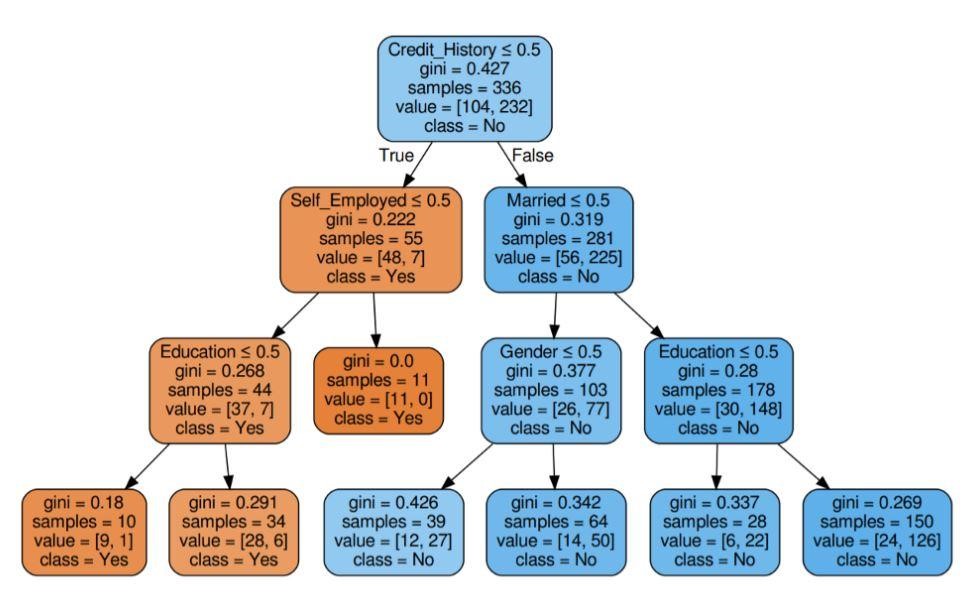Kaynak

Şekil 6: Kriter entropisi olan karar ağacı

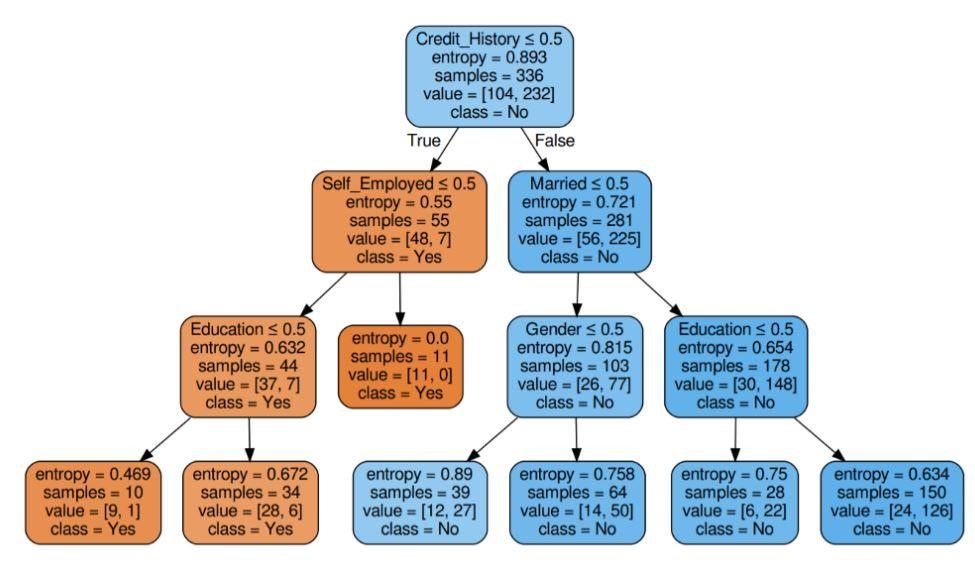
Kaynak

Adım 6: Modelin puanını kontrol edin

Neredeyse yüzde 80 doğruluk puanlandı.

Uygulama Listesi

Karar ağaçları çoğunlukla bilgi uzmanları tarafından analitik bir araştırma yapmak için kullanılır. Zorlukları analiz etmek veya tahmin etmek için ticari amaçlarla yaygın olarak kullanılabilirler. Karar ağacının esnekliği, farklı bir alanda kullanılmalarına olanak tanır:

1. Sağlık

Karar ağaçları, bir hastanın yaş, kilo, cinsiyet vb. koşullarla belirli bir hastalıktan muzdarip olup olmadığının tahmin edilmesini sağlar. Diğer tahminler, ilacın etkisine kompozisyon, üretim süresi vb. gibi faktörleri göz önünde bulundurarak karar vermeyi içerir.

2. Bankacılık sektörleri

Karar ağaçları, bir kişinin mali durumu, maaşı, aile üyeleri vb. dikkate alınarak krediye uygun olup olmadığının tahmin edilmesine yardımcı olur. Ayrıca kredi kartı sahtekarlıklarını, kredi temerrütlerini vb. tespit edebilir.

3. Eğitim Sektörleri

Bir öğrencinin başarı puanına, devamına vb. göre kısa listeye alınması karar ağaçları yardımıyla kararlaştırılabilir.

Avantajların Listesi

• Bir karar modelinin yorumlanabilir sonuçları, üst yönetime ve paydaşlara sunulabilir.
• Karar ağacı modeli oluşturulurken verilerin ön işlenmesi yani normalizasyon, ölçekleme vb. gerekli değildir.
• Hem sayısal hem de kategorik veri türü, diğer algoritmalara göre daha yüksek kullanım verimliliğini gösteren bir karar ağacı tarafından ele alınabilir.
• Verideki eksik değer, karar ağacının sürecini etkilemez ve bu nedenle onu esnek bir algoritma haline getirir.

Sıradaki ne?

Veri madenciliğinde uygulamalı deneyim kazanmak ve uzmanlar tarafından eğitilmekle ilgileniyorsanız, upGrad'ın Veri Biliminde Yönetici PG Programına göz atabilirsiniz. Kurs, mezuniyette en az %50 veya eşdeğeri geçme notu olan 21-45 yaş arasındaki herhangi bir yaş grubuna yöneliktir. Herhangi bir çalışan profesyonel, IIIT Bangalore sertifikalı bu yönetici PG programına katılabilir.