Bayesyen Düşünce Nedir? Giriş ve Teorem

İngiliz istatistikçi ve filozof Thomas Bayes tarafından 1700'lerde verilen istatistiksel bir teorem, dünyanın her yerindeki bilim adamları ve analistler için yol gösterici bir ışık olmaya devam ediyor. Bugün Bayesci düşünce tıpta, bilimde, teknolojide ve diğer birçok disiplinde uygulama bulmakta ve dünya görüşümüzü ve bunun sonucunda ortaya çıkan eylemlerimizi güçlü bir şekilde etkilemeye devam etmektedir.

Thomas'ın Bayes fikri çarpıcı biçimde basitti. Bayes'e göre, bir hipotezin doğru olma olasılığı iki koşula bağlıdır: Halihazırda bildiklerimize (önceki bilgilere) dayanarak ne kadar makul olduğu ve yeni kanıtlara ne kadar uyduğu. Bu nedenle, Bayesci düşünme, geleneksel hipotez testlerinden, birincisinin, sonuçlara atlamadan önce ön bilgileri içermesi bakımından farklıdır.

Ön girişi göz önünde bulundurarak, Bayes istatistikleri hakkında biraz daha ayrıntıya girelim.

Bayes İstatistikleri

Basit bir ifadeyle, Bayes istatistikleri, yeni verilerin kanıtları ışığında önceki inançları güncellemek için istatistiksel problemlere olasılıklar uygular. Olasılık, belirli bir olaya olan inancın derecesini ifade eder.

İnanç derecesi, kişisel varsayımlara veya önceki deneylerin sonuçlarına dayalı olarak olayla ilgili önceki bilgilere dayanabilir. Bayes istatistikleri, olasılıkları hesaplamak için Bayes Teoremini kullanır. Bayes Teoremi, sırayla, olayla ilgili yeni kanıtlara ve önceki bilgilere dayanan bir olayın koşullu olasılığını tanımlar.

Bunu akılda tutarak, Bayes Teoremini derinlemesine anlamadan önce koşullu olasılığın temel kavramını tazeleyelim.

Şartlı olasılık

Koşullu olasılık, önceki bir olayın veya sonucun meydana gelmesine bağlı olarak bir olayın veya sonucun olasılığı olarak tanımlanabilir. Önceki olayın olasılığı ile sonraki veya koşullu olayın olasılığı çarpılarak hesaplanır.

Konsepti daha iyi anlamak için bir örneğe bakalım .

• A Olayı, gezi planlayan bir ailenin pikniğe gitmesidir. Ailenin pikniğe gitme olasılığı %80'dir.
• B olayı, ailenin pikniğe gittiği gün yağmur yağacak olmasıdır. Hava tahmini, piknik gününde yağış olasılığının %60 olduğunu söylüyor.
• Buna göre, ailenin pikniğe gitmesi ve yağmur yağması olasılığı (P) şu şekilde hesaplanır:

P (Piknik ve yağmur) = P (Yağmur | Piknik) P (Piknik) = (0,60) * (0,80) = 0,48

Yukarıdaki örnekte, koşullu olasılık, A ve B olaylarının birbiriyle ilişkisine, yani ailenin pikniğe gitmesi ve aynı gün yağmur yağması olasılığına bakar.

Bu nedenle, koşullu olasılık koşulsuz olasılıktan farklıdır, çünkü ikincisi, başka herhangi bir olay veya olayın meydana gelip gelmediğine veya başka herhangi bir koşulun mevcut olup olmadığına bakılmaksızın bir olayın meydana gelme olasılığını ifade eder.

Koşullu olasılık formülü

Koşullu olasılık formülü, olasılık çarpma kuralından gelir:

P (A ve B) veya P (AUB) = P ( A verilen B) veya P (B | A) * P (A)

Yukarıdaki denklemde, P (A ve B), aynı anda meydana gelen iki veya daha fazla olayın olasılığına atıfta bulunan ortak olasılıktır. P(A,B) şeklinde de yazılır.

Çarpım kuralından koşullu olasılık denkleminin nasıl çıkarılacağı aşağıda açıklanmıştır:

Adım 1: Çarpma kuralını yazın.

P (A ve B) = P (B | A) * P (A)

Adım 2: Denklemin her iki tarafını da P(A)'ya bölün.

P (A ve B) / P (A) = P (B | A) * P (A) / P (A)

Adım 3: Denklemin sağ tarafındaki P'yi (A) iptal edin.

P (A ve B) / P (A) = P (B | A)

Adım 4: Denklemi yeniden yazın.

P (A ve B) = P (B | A) / P (A)

Böylece, koşullu olasılık formülü şu şekilde verilir:

P (A ve B) = P (B | A) / P (A)

Bayes teoremi

Bayes Teoremini kullanarak, yeni ve ilgili kanıtlara dayalı olarak inançlarımızı ve kanaatlerimizi güncelleyebiliriz. Örneğin, belirli bir kişinin kanser olma olasılığını bulmaya çalışıyorsak, bunun genellikle nüfusun kanserli yüzdesi olduğunu varsayarız. Bununla birlikte, söz konusu kişinin düzenli bir sigara içicisi olduğu gibi ekstra kanıtlar sunarsak, bir kişi sigara içiyorsa kanser olma olasılığı daha yüksek olduğu için algımızı (ve dolayısıyla olasılığımızı) güncelleyebiliriz. Bu nedenle, tahminlerimizi geliştirmek için hem ön bilgimizi hem de ek kanıtları kullanırız.

Bayes Teoreminin formülü

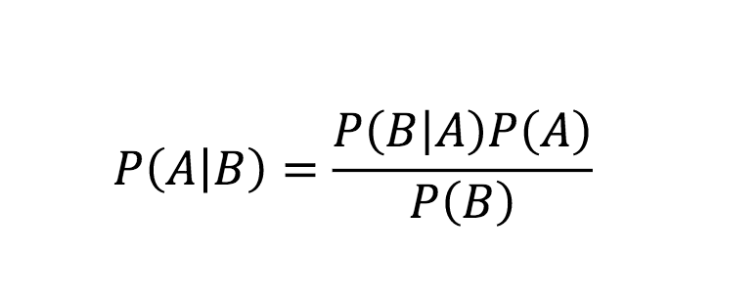
Kaynak

Yukarıdaki denklem Bayes kuralıdır. Şimdi, Bayes Teoremi denkleminin adım adım türetilmesine bakalım.

Adım 1: İki olayı ele alalım, A ve B. A, olasılığını hesaplamak istediğimiz olaydır ve B, A ile ilgili ek kanıttır.

Adım 2: A ve B olaylarının ortak olasılığı ile koşullu olasılığı arasındaki ilişkiyi yazın.

P (A,B) = P (A | B) * P(B) = P (B,A) = P (B | A) * P(A)

Adım 3: İki koşullu olasılık terimini birbirine eşitleyin.

P (A | B) * P(B) = P (B | A) * P(A)

Adım 4: Denklemin her iki tarafını da P(B)'ye bölün.

P (A | B) * P(B) / P (B) = P (B | A) * P(A) / P (B)

Adım 5: Denklemin sol tarafındaki P'yi (B) iptal edin.

P (A | B) = P (B | A) * P(A) / P (B)

Böylece Bayes Teoremi formülünü aşağıdaki gibi elde ederiz:

P (A | B) = P (B | A) * P(A) / P (B)

Bayes Teoremi denklemindeki terimleri anlama

P (A | B) = P (B | A) * P(A) / P (B)

• P (A | B) , sonsal olasılık veya tahmin etmeye çalıştığımız olasılık olarak adlandırılır. Önceki örneğe dayanarak, kişinin düzenli bir sigara içicisi olduğu göz önüne alındığında, sonraki olasılık kişinin kanser olma olasılığı olacaktır.
• P (B | A) , ilk hipotezimiz göz önüne alındığında, ek kanıtları tespit etme olasılığına atıfta bulunarak olabilirlik olarak adlandırılır . Yukarıdaki örnekte, kişinin kanser olduğu göz önüne alındığında, kişinin sigara içiyor olma olasılığıdır.
• P (A) , herhangi bir ek kanıt veya bilgi olmadan hipotezimizin önceki olasılığı veya olasılığıdır. Yukarıdaki örnekte, önceki olasılık kanser olma olasılığıdır.
• P (B) kanıtı gözlemlemenin marjinal olasılığı veya toplam olasılığıdır. Yukarıdaki örnek bağlamında, marjinal olasılık, sigara içiyor olma olasılığıdır.

Bayes Teoremini Anlamak İçin Basit Bir Örnek

Önceki örnekte bazı varsayımsal sayıları kullanarak, Bayes Teoremini uygulamanın etkisini göreceğiz.

Diyelim ki kanser olma olasılığı 0.06, yani insanların %6'sında kanser var. Şimdi, sigara içenlerin olma olasılığının 0.20 veya insanların %20'sinin sigara içtiğini ve kanserli kişilerin %30'unun sigara içtiğini varsayalım. Yani, P (Sigara İçen | Kanser) = 0.30.

Başlangıçta kanser olma olasılığı basitçe 0,06'dır (önceki). Ancak yeni kanıtları kullanarak, P (Kanser | Sigara içen) = P ((Sigara İçen | Kanser) * P (Kanser)) / P (Sigara İçen) = (0.30*0.06) / (0.20) = 0.09'u hesaplayabiliriz.

Dünyanın en iyi Üniversitelerinden çevrimiçi veri bilimi kursları öğrenin . Kariyerinizi hızlandırmak için Yönetici PG Programları, Gelişmiş Sertifika Programları veya Yüksek Lisans Programları kazanın.

İleriye Doğru: Veri Bilimi veya Makine Öğreniminde Bir Kariyer için İstatistik Kavramlarında Ustalaşın

upGrad'ın yüksek EdTech öğrenme platformu, çok sayıda kursu ve kapsamlı öğrenme deneyimleri ile dünya çapında 500.000'den fazla çalışan profesyoneli etkiledi. 85'ten fazla ülkeye yayılmış 40.000'den fazla öğrenci tabanı ile upGrad'ın sektörle ilgili kurslarının, kariyerinizi seçtiğiniz alanda ilerletmesi garanti edilmektedir.

Veri Biliminde Yüksek Lisans, İstatistik, Tahmine Dayalı Analiz, Makine Öğrenimi, Büyük Veri Analitiği, Veri Görselleştirme vb. alanlarda temel beceriler kazandıran 18 aylık bir kurstur.

Programın Öne Çıkanları:

• Liverpool John Moores Üniversitesi'nden Yüksek Lisans Derecesi ve IIIT Bangalore'dan Yönetici PGP
• 500 saatten fazla içerik, 60'tan fazla vaka çalışması ve proje, 20'den fazla canlı oturum, 14'ten fazla programlama dili ve aracı
• Endüstri ağı, şüphe çözme oturumları ve öğrenme desteği

Makine Öğrenimi ve Derin Öğrenmede İleri Düzey Sertifika Programı, akran ağı oluşturma fırsatları, uygulamalı projeler, endüstri danışmanlığı ve 360 ​​derecelik kariyer desteği ile 6 aylık zorlu bir kurstur.

Programın Öne Çıkanları:

• IIIT Bangalore'den prestijli tanıma
• 240+ saat içerik, 5+ vaka çalışması ve proje, 24+ canlı oturum, 12 programlama dili, araç ve kitaplık kapsamı
• Sektör uzmanlarıyla 1:8 grup koçluğu seansları ve 1:1 mentorluk seansları

Çözüm

Bayesçi düşünce, çoğumuz farkında olmasak da, insan düşüncesinin, sorgulamasının ve inancının çeşitli alanlarının temelini oluşturur. Kanser taraması ve küresel ısınmadan para politikasına ve risk değerlendirmesi ve sigortaya kadar Bayesçi düşünce esastır. Ünlü İngiliz matematikçi Alan Turing'in bile , İkinci Dünya Savaşı sırasında Alman Enigma Kodunu kırmak için Bayes yaklaşımını kullandığına inanılıyor.

upGrad'a kaydolun ve temel istatistiksel kavramlar ve daha fazlası hakkında bilginizi artırın!