Veri Yapısındaki Ağaçlar: Her Veri Bilimcisinin Bilmesi Gereken 8 Ağaç Türü

Tanıtım

Bilgi işlem alanında, veri yapıları, uygun depolama ve görüntüleme sağlayan bir disk üzerindeki veri düzenleme modeline atıfta bulunur. 2021'de kazançlı bir kariyer seçimi olacağı tahmin edilen veri bilimi alanıyla ilgililer. Önümüzdeki birkaç yıl için tahminlere dayanarak, büyük ölçekli derin öğrenme modelleri ve yeni nesil akıllı cihazlar geleceğin kapılarını açacak. bu sektör.

Bu nedenle, teknolojik ilerlemenin ortasında uygun bir kariyer bulmak için veri yapıları bilgisini edinmek gerekli olacaktır. 2021 Veri Bilimi Endüstrisi tahminine göre, ABD ve Hindistan, 250.000'den fazla firmada yaklaşık 50000 veri bilimcisi ve 300.000 veri analisti istihdam edecek. [1]

Veri yapıları, bilginin tahsisi, yönetimi ve geri alınması için yolları tasarlamak için uygulanır. Veri yapıları, genel olarak işlenmiş verilerin verimliliğinin taslağının hazırlanması ve iyileştirilmesi için özellikle gereklidir. Bilgi alışverişini etkin bir şekilde kolaylaştırmak için verileri gruplandırarak ve düzenleyerek yönetirler.

Veri Yapılarındaki Ağaçlar

'Ağaçlar', veri tahsisi için hiyerarşik bir model izleyen bir ADT (Özet Veri Türleri) türüdür. Temel olarak, bir ağaç, kenarlar aracılığıyla birbirine bağlanan çoklu düğümlerin bir koleksiyonudur. Bu 'ağaçlar', bir ağaca benzeyen bir veri yapısı tasarımı oluşturur; burada 'kök' düğüm, 'ana' düğümlere ve sonunda 'alt' düğümlere yol açar . Bağlantılar 'kenar' olarak bilinen çizgilerle yapılır.

'Yaprak' düğümleri, onlardan kaynaklanan başka alt düğümleri olmayan uç noktalardır. Veri yapılarındaki ağaçlar , düzenlemelerinin doğrusal olmayan doğası nedeniyle hayati bir rol oynar. Bu, tasarım aşamaları boyunca kolaylık ile birlikte bir arama sırasında daha hızlı yanıt süresi sağlar.

Veri Yapısındaki Ağaç Türleri

Veri yapılarındaki çeşitli ağaç türleri aşağıda ayrıntılı olarak açıklanmıştır:

1. Genel Ağaç

Genel bir ağaç, bir düğümün sahip olabileceği çocuk sayısı üzerinde herhangi bir spesifikasyonun veya kısıtlamanın olmaması ile karakterize edilir. Hiyerarşik yapıya sahip herhangi bir ağaç, genel bir ağaç olarak sınıflandırılabilir. Bir düğümün birden fazla çocuğu olabilir ve ağacın oryantasyonu için herhangi bir kombinasyon olabilir. Düğümler 0'dan n'ye kadar herhangi bir derecede olabilir.

Aşağıda, en üstte '2'nin kök düğüm olduğu, veri yapısındaki genel bir ağacın klasik bir örneği verilmiştir.

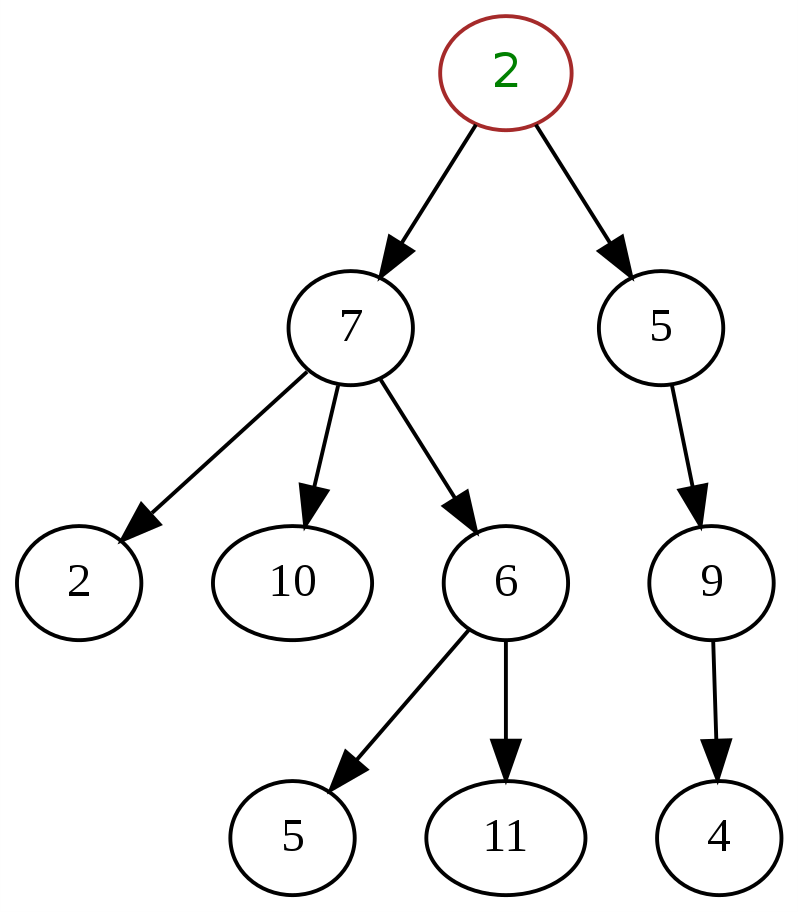
Kaynak

2. İkili Ağaç

İki sayı anlamına gelen 'ikili' kelimesiyle tanımlandığı gibi, bir ikili ağaç 2 alt düğüme sahip olabilen düğümlerden oluşur. İkili ağaçtaki herhangi bir düğüm en fazla 0, 1 veya 2 düğüme sahip olabilir. Veri yapılarındaki ikili ağaçlar oldukça işlevsel ADT'lerdir ve birçok türe ayrılabilirler. Öncelikle veri yapılarında iki amaç için kullanılırlar:

1. İkili Arama Ağaçlarında gözlemlendiği gibi düğümlere erişmek ve onları etiketlemek için.
2. Bir çatallı yapı aracılığıyla verilerin temsili için.

Aşağıdaki, bir veri yapısındaki bir ikili ağacın temel diyagramıdır:

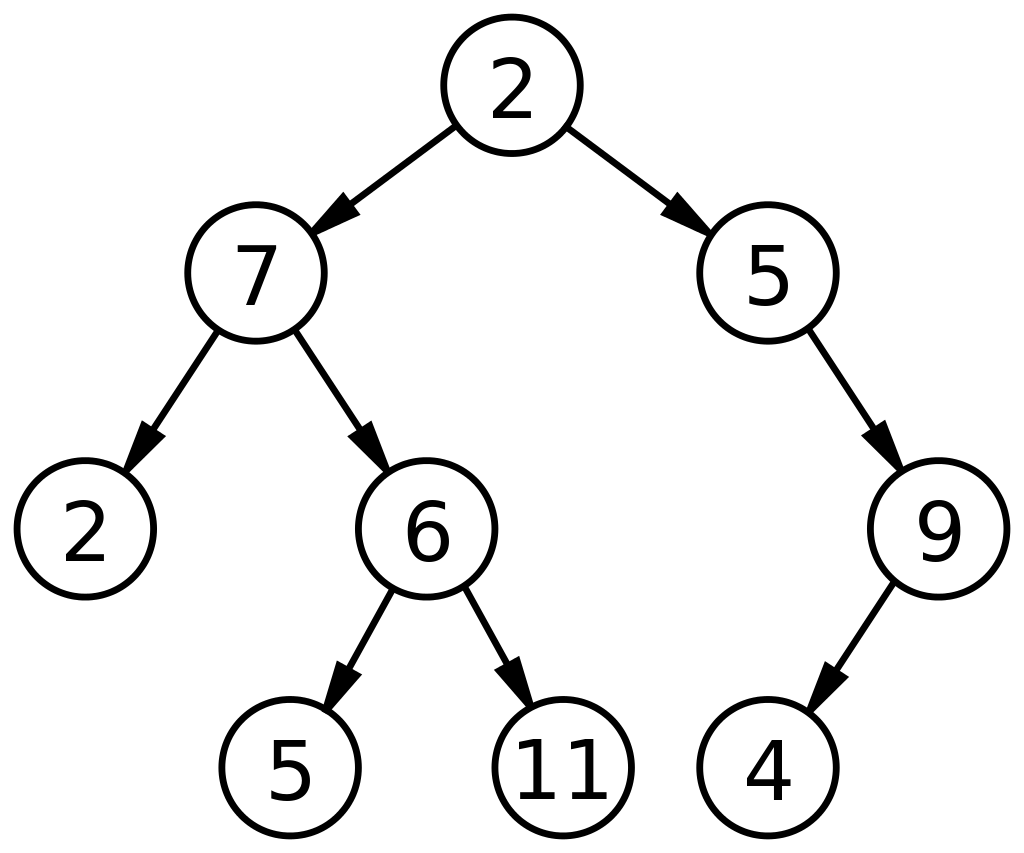
Kaynak

3. İkili Arama Ağacı

İkili Arama Ağacı (BST), daha hızlı arama/arama veya veri ekleme/kaldırma işlemlerini kolaylaştıracak şekilde düzenlenmiş benzersiz bir ikili ağaç alt türüdür. Bir BST, üç alana dayalı olarak düğümlerin temsili ile tanımlanır: veri, sol çocuğu ve sağ çocuğu. BST için yönetim faktörleri şunlardır:

1. Sol taraftaki (sol alt) her düğüm, üst düğümünden daha küçük bir değere sahip olmalıdır.
2. Sağ taraftaki (sağ alt) her düğüm, üst düğümünden daha yüksek bir değere sahip olmalıdır.

Böyle bir düzenleme, bir dizide olduğu gibi arama sürelerini doğrusal bir aramanın yarısına düşürür. Bu nedenle, veri yapılarındaki ikili arama ağaçları, diğer ADT'lere kıyasla arama ve sıralama için yaygın olarak uygulanabilir.

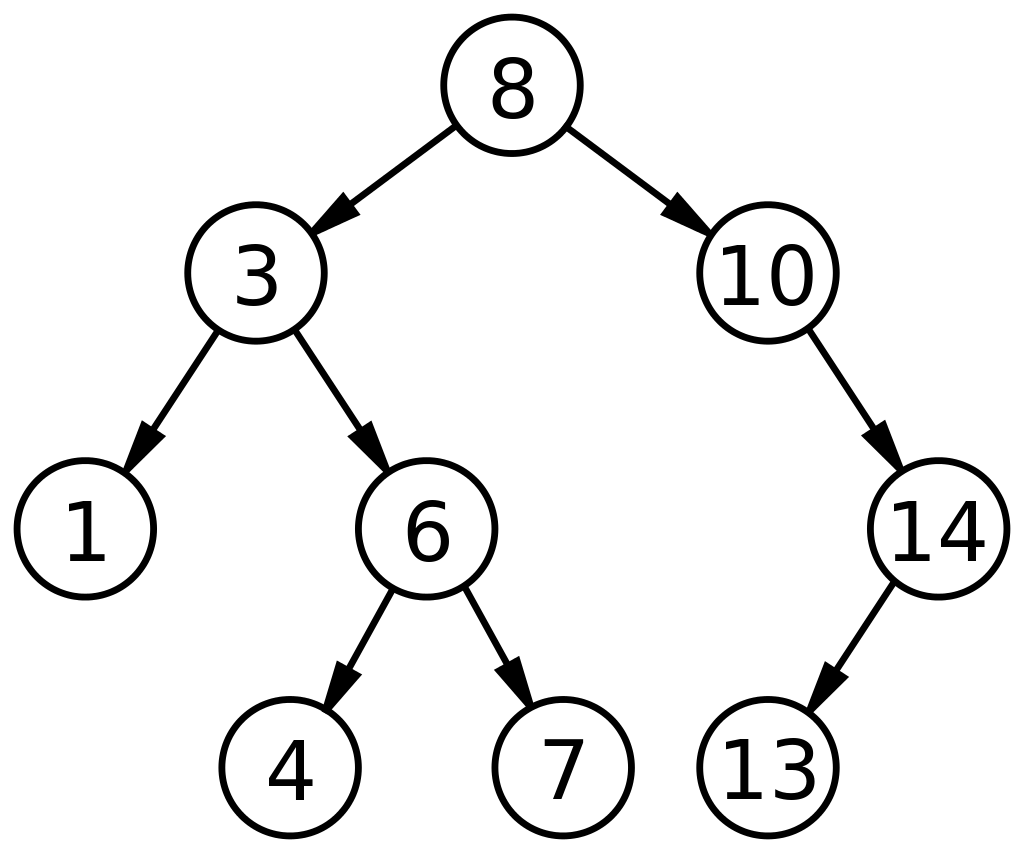
Kaynak

Hem BT'ler hem de BST'ler veri yapılarında esasen ağaçlar olsa da , adlarındaki benzerlikten dolayı kafanız karışmasın. Bir ikili ağaç ve bir ikili arama ağacı arasındaki farkı upGrad'da ayrıntılı olarak öğrenin .

4. AVL Ağacı

AVL ağacı, adını mucitlerinden Adelson-Velsky ve Landis'ten alır. AVL ağacı, kendi kendini dengeleyen bir yapıya sahiptir. Kök düğümlerinin iki alt ağacının yükseklikleri ikiden az ile sınırlandırılmıştır. Yükseklik farkı 1'in üzerine çıktığında, alt düğümler yeniden dengelenir.

AVL ağaçları yükseklik dengelidir ve bu yeniden dengeleme tek veya çift dönüşlerle gerçekleşir. Dengeleme faktörü, sol alt ağaç ile sağ alt ağacın yükseklikleri arasındaki farktır ve değerler -1, 0 ve 1'dir.

5. Kırmızı Kara Ağaç

Bu tür, kırmızı siyah ağaçların da yüksekliği dengeli olduğu için AVL ağaçlarına benzer. Onları ayıran şey, onları dengelemek için ikiden fazla rotasyon gerektirmemesidir. Bir düğümün kırmızı veya siyah rengini tanımlayan fazladan bir bit içerirler, bu da silme ve ekleme sırasında ağaçların dengelenmesini sağlar. Kırmızı siyah renk kodlaması da değişiklikler sırasında yeniden boyanır, ancak neredeyse hiçbir ek bellek maliyeti yoktur.

6. Yayılma Ağacı

İkili arama ağacının başka bir alt türü olan yayılma ağacı, son düğümü ayarlamak için rotasyonel işlemler gerçekleştirme gibi benzersiz bir özelliğe sahiptir. En son erişilen düğüm, bir döndürme yapılarak kök düğüm olarak düzenlenir. Dengeli bir ağaçtır, ancak yüksekliği dengeli değildir.

Ağaç döndürmeler belirli bir şekilde gerçekleştirildiği için, ilk ikili ağaç aramasından sonra 'yayılma' eylemi gerçekleştirilir. Her işlemden sonra ağaç kendini dengelemek için döndürülür ve aranan eleman bir kök düğüm olarak en üste yerleştirilir.

7. Treap

Veri yapılarındaki 'Treap'ler, ağaçların ve yığınların birleşimidir. BST'lerde sol çocuğun değeri kök düğümden küçük, sağ çocuğun değeri ise daha yüksek olmalıdır. Bir yığın veri yapısında, kök düğüm en düşük değere sahiptir ve alt düğümleri (hem sol hem de sağ) daha büyük değerlere sahiptir.

Böylece, treap bir anahtar (BST'lere benzeyen) ve bir öncelik (yığınlar gibi) biçiminde bir değere sahiptir. En yüksek öncelikli düğümler, önce ikili arama ağacına, öncelik sayıları bağımsız rastgele sayılar olacak şekilde eklenir. Dinamik bir sıralı anahtar seti tutarlar ve anahtarlarında ikili aramalara izin verirler.

8. B-Ağacı

Veri yapılarında kendi kendini dengeleyen bir ağaç türü olarak B-Tree, logaritmik zamanda aramaya, sıralı erişime, silmelere ve eklemelere izin vermek için verileri sıralar. Bir ikili ağacın aksine, bir B ağacı, düğümlerinin ikiden fazla çocuğa sahip olmasına izin verir. Daha büyük veri bloklarını okuyan ve yazan veritabanları ve dosya sistemleriyle uyumludurlar.

Veri yapılarında bir B ağacı, diskler gibi daha büyük depolama sistemleri için kullanılır. Tüm yapraklar bilgi taşımaz ve aynı seviyede görünürler. Bir B ağacının dahili düğümleri, bir aralığa bağlı değişken boyutta alt düğümlere sahip olabilir.

Bunlar, veri akışını tasarlayan programcılar tarafından uygulanan veri yapılarındaki ağaçlardır . Benzersiz özelliklerini ve uygulamalarını öğrenmek, veri bilimcisi olma yolculuğunuz için çok önemlidir. Kendinizi geliştirmenin başka bir yöntemi , veri yapılarındaki ve diğer ADT formlarındaki ağaçların bilgisini gerektiren çeşitli projeler aracılığıyla pratik yapmak olacaktır .

Bilginizi DS projelerine uygulamak için, aşağıdaki blog bağlantılarında yeni başlayanlar için 13 ilginç veri yapısı proje fikri ve konusu vardır [2021] .

Çözüm

Bir veri yapısındaki ağaçlar gibi kavramları öğrenmek zor olabilir ve programlama adaylarının kendilerini eğitmek için uzman rehberliğine ihtiyacı vardır. Bir veri yapısındaki ağaçlar hakkında daha fazla bilgi edinmek için upGrad'ın çevrimiçi kurslarına göz atın . Yazılım Geliştirmede Yönetici PG Programı – IIIT-B & upGrad tarafından DevOps ile DevOps'ta Uzmanlaşma, bir programcı olarak kariyerinizi geliştirmenize yardımcı olabilir.

Veri yapılarının yeterliliği kodlama sürecinin ayrılmaz bir parçası olduğundan, öğrencinin uzman bir programcı ve yazılım geliştiricisi olmasına yardımcı olabilir. Programcılar ve veri bilimcileri, önümüzdeki on yıllar boyunca talep görecekler .

Hindistan'da, talebi karşılamak için binlerce veri bilimcinin istihdam edilmesini gerektiren büyük miktarda veri üreten ve tüketen 500 milyon internet kullanıcımız var. [2] Bu veri bilimcilerin, bu sektörde iş aramak için ilgili teknolojik uzmanlığa sahip doğru eğitime ihtiyaçları vardır.

UpGrad & IIIT-Bangalore tarafından düzenlenen Yazılım Geliştirmede Yönetici PG Programı – Tam Yığın Geliştirmede Uzmanlaşma, profilinizi geliştirmenize ve bir programcı olarak daha iyi istihdam fırsatları sağlamanıza yardımcı olabilir .