Makine Öğrenimi İçin Naive Bayes Algoritmasını Öğrenin [Örneklerle]
Yayınlanan: 2021-02-25İçindekiler
Tanıtım
Matematik ve programlamada, en basit çözümlerden bazıları genellikle en güçlü olanlardır. Saf Bayes Algoritması, bu ifadenin klasik bir örneği olarak gelir. Makine Öğrenimi alanındaki güçlü ve hızlı ilerleme ve gelişmelere rağmen, bu Naive Bayes Algoritması, en yaygın kullanılan ve verimli algoritmalardan biri olarak hala güçlüdür. Saf Bayes Algoritması, uygulamalarını Sınıflandırma görevleri ve Doğal Dil İşleme (NLP) sorunları dahil olmak üzere çeşitli problemlerde bulur.
Bayes Teoreminin matematiksel hipotezi, bu Naive Bayes Algoritmasının arkasındaki temel kavram olarak hizmet eder. Bu yazıda, Naive Bayes Algoritması olan Bayes Teoreminin temellerini ve Python'da gerçek zamanlı bir örnek problemle uygulamasını inceleyeceğiz. Bunların yanı sıra Naive Bayes Algoritmasının rakiplerine göre bazı avantaj ve dezavantajlarına da bakacağız.
Olasılığın Temelleri
Bayes Teoremi ve Naive Bayes Algoritmasını anlamaya girişmeden önce, Olasılığın temelleri üzerine mevcut bilgilerimizi tazeleyelim.
Hepimizin tanım gereği bildiği gibi, bir A olayı verildiğinde, o olayın meydana gelme olasılığı P(A) ile verilir. Olasılıkta, A olayının meydana gelmesi, B olayının meydana gelme olasılığını değiştirmiyorsa ve bunun tersi de, iki A ve B olayı bağımsız olaylar olarak adlandırılır. Öte yandan, birinin meydana gelmesi diğerinin olasılığını değiştirirse, bunlara Bağımlı olaylar denir.
Koşullu Olasılık adlı yeni bir terimle tanışalım . Matematikte, P (A| B) tarafından verilen iki A ve B olayı için Koşullu Olasılık, B olayının zaten meydana geldiği göz önüne alındığında, A olayının meydana gelme olasılığı olarak tanımlanır. A ve B olaylarının bağımlı mı yoksa bağımsız mı oldukları arasındaki ilişkiye bağlı olarak, Koşullu Olasılık iki şekilde hesaplanır.
- İki bağımlı A ve B olayının koşullu olasılığı, P (A| B) = P (A ve B) / P (B) ile verilir.
- İki bağımsız A ve B olayının koşullu olasılığı için ifade , P (A| B) = P (A) ile verilir.
Olasılık ve Koşullu Olasılıkların arkasındaki matematiği bilerek, şimdi Bayes Teoremi'ne geçelim.

Bayes teoremi
İstatistik ve olasılık teorisinde, Bayes kuralı olarak da bilinen Bayes Teoremi, olayların koşullu olasılığını belirlemek için kullanılır. Başka bir deyişle, Bayes teoremi, olayla ilgili olabilecek koşulların ön bilgisine dayalı olarak bir olayın olasılığını tanımlar.
Bunu daha basit bir şekilde anlamak için, bir evin fiyatının çok yüksek olma olasılığını bilmemiz gerektiğini düşünün. Yakınlarda okul, sağlık ocağı ve hastanelerin varlığı gibi diğer parametreleri de bilirsek, daha doğru bir değerlendirme yapabiliriz. Bayes Teoremi tam olarak bunu gerçekleştirir.
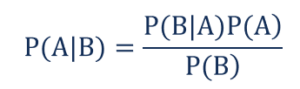
Öyle ki,
- P(A|B) – B olayının gerçekleşmesi durumunda A olayının gerçekleşmesinin koşullu olasılığı, Arka Olasılık olarak da bilinir .
- P(B|A) – A olayının gerçekleşmesi durumunda B olayının gerçekleşmesinin koşullu olasılığı, Olabilirlik Olasılığı olarak da bilinir .
- P(A) – Ön Olasılık olarak da bilinen A olayının gerçekleşme olasılığı.
- P(B) – Marjinal Olasılık olarak da bilinen B olayının gerçekleşme olasılığı.
'n' bağımsız değişkenli basit bir Makine Öğrenimi problemimiz olduğunu ve çıktı olan bağımlı değişkenin bir Boole değeri (Doğru veya Yanlış) olduğunu varsayalım. Bağımsız niteliklerin doğası gereği kategorik olduğunu varsayalım, bu örnek için 2 kategori düşünelim. Dolayısıyla, bu verilerle Olabilirlik Olasılığının değerini, P(B|A) hesaplamamız gerekiyor.
Bu nedenle, yukarıdakileri gözlemlediğimizde, bu Machine Learning modelini öğrenmek için 2*(2^ n -1 ) parametresini hesaplamamız gerektiğini görüyoruz . Benzer şekilde, 30 Boole bağımsız özniteliğimiz varsa, hesaplanacak toplam parametre sayısı 3 milyara yakın olacaktır ki bu da hesaplama maliyeti açısından son derece yüksektir.
Bayes Teoremi ile bir Makine Öğrenimi modeli oluşturmadaki bu zorluk, Naive Bayes Algoritmasının doğuşuna ve geliştirilmesine yol açtı.
Naive Bayes Algoritması
Pratik olması için Bayes Teoreminin yukarıda belirtilen karmaşıklığının azaltılması gerekir. Bu, tam olarak Naive Bayes Algoritması'nda birkaç varsayım yaparak elde edilir. Yapılan varsayımlar, her özelliğin sonuca bağımsız ve eşit bir katkı sağladığı yönündedir.
Naive Bayes Algoritması, denetimli bir öğrenme algoritmasıdır ve öncelikle sınıflandırma problemlerinin çözümünde kullanılan Bayes teoremine dayanmaktadır. Hızlı tahminler yapmak için Makine Öğrenimi modelleri oluşturan en basit ve en doğru Sınıflandırıcılardan biridir. Matematiksel olarak, olayların olasılık fonksiyonunu kullanarak tahminler yaptığı için olasılıksal bir sınıflandırıcıdır.
Örnek Problem
Varsayımların arkasındaki mantığı anlamak için daha iyi bir sezgi elde etmek için basit bir veri kümesinden geçelim.
| Renk | Tip | Menşei | Çalınması? |
| Siyah | Sedan | İthal | Evet |
| Siyah | SUV | İthal | Numara |
| Siyah | Sedan | Yerel | Evet |
| Siyah | Sedan | İthal | Numara |
| kahverengi | SUV | Yerel | Evet |
| kahverengi | SUV | Yerel | Numara |
| kahverengi | Sedan | İthal | Numara |
| kahverengi | SUV | İthal | Evet |
| kahverengi | Sedan | Yerel | Numara |
Yukarıda verilen veri setinden, yukarıda Naive Bayes Algoritması için tanımladığımız iki varsayımın kavramlarını türetebiliriz.
- İlk varsayım, tüm özelliklerin birbirinden bağımsız olduğudur. Burada “Kırmızı” renginin arabanın Tipi ve Menşeinden bağımsız olması gibi her özelliğin bağımsız olduğunu görüyoruz.
- Daha sonra, her bir özelliğe eşit önem verilecektir. Benzer şekilde, sadece Arabanın Türü ve Menşei hakkında bilgi sahibi olmak, sorunun çıktısını tahmin etmek için yeterli değildir. Bu nedenle, değişkenlerin hiçbiri alakasız değildir ve bu nedenle hepsi sonuca eşit katkıda bulunur.
Özetlemek gerekirse, A ve B, C verildiğinde koşullu olarak bağımsızdır, ancak ve ancak, C'nin meydana geldiği bilgisi göz önüne alındığında, A'nın oluşup oluşmadığına dair bilgi, B'nin meydana gelme olasılığı hakkında hiçbir bilgi sağlamaz ve B'nin gerçekleşip gerçekleşmediğine ilişkin bilgi, bu konuda hiçbir bilgi sağlamazsa. A'nın gerçekleşme olasılığı. Bu varsayımlar Bayes algoritmasını – Naive yapar . Naive Bayes Algoritması adını buradan alır.
Dolayısıyla yukarıda verilen problem için Bayes Teoremi şu şekilde yeniden yazılabilir:
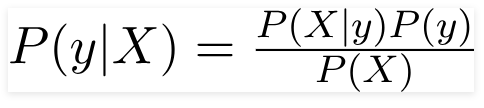
Öyle ki,
- Arabanın Rengi, Tipi ve Menşei gibi özellikleri temsil eden bağımsız özellik vektörü, X = (x 1 , x 2 , x 3 ……x n ) .
- Çıktı değişkeni, y'nin yalnızca iki sonucu Evet veya Hayır vardır.
Bu nedenle, yukarıdaki değerleri değiştirerek Naive Bayes Formülünü şu şekilde elde ederiz:
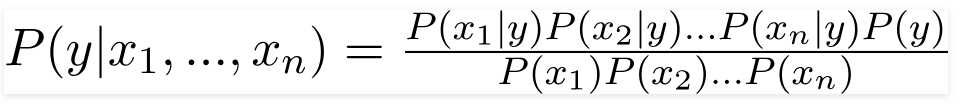
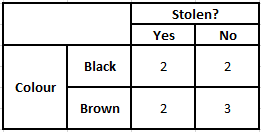
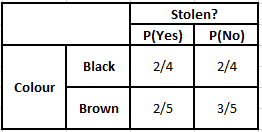
Sonsal olasılığı P(y|X) hesaplamak için, çıktıya karşı her öznitelik için bir Frekans Tablosu oluşturmamız gerekir. Ardından, frekans tablolarını Olabilirlik Tablolarına dönüştürdükten sonra, her bir sınıf için sonsal olasılığı hesaplamak için Naive Bayes denklemini kullanıyoruz. Sonsal olasılığı en yüksek olan sınıf, tahminin sonucu olarak seçilir. Aşağıda, üç tahmin edicinin tümü için Sıklık ve olabilirlik tabloları bulunmaktadır.
Renk Olasılık Tablosu Renk Sıklık Tablosu
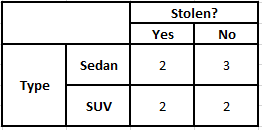
Tip Olasılık Tablosu Tip Sıklık Tablosu
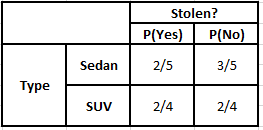

Menşe Sıklık Tablosu Menşe Olabilirlik Tablosu
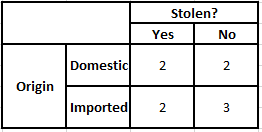
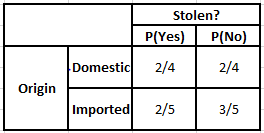
Aşağıda verilen koşullar için sonsal olasılıkları hesaplamamız gereken durumu düşünün -
| Renk | Tip | Menşei |
| kahverengi | SUV | İthal |
Böylece, yukarıda verilen formülden, aşağıda gösterildiği gibi Arka Olasılıkları hesaplayabiliriz.
P(Evet | X) = P(Kahverengi | Evet) * P(SUV | Evet) * P(İthal | Evet) * P(Evet)
= 2/5 * 2/4 * 2/5 * 1
= 0.08
P(Hayır | X) = P(Kahverengi | Hayır) * P(SUV | Hayır) * P(İthal | Hayır) * P(Hayır)
= 3/5 * 2/4 * 3/5 * 1
= 0.18
Yukarıda hesaplanan değerlerden Hayır için Arka Olasılıklar Evet'ten Büyük (0.18>0.08) olduğundan, Kahverengi Renkli, SUV Tipi İthal Menşeli bir otomobilin “Hayır” olarak sınıflandırıldığı çıkarılabilir. Bu nedenle araç çalıntı değildir.
Python'da Uygulama
Naive Bayes algoritmasının arkasındaki matematiği anladığımıza ve bir örnekle görselleştirdiğimize göre, Python dilinde Makine Öğrenimi kodunu inceleyelim.
İlgili: Naive Bayes Sınıflandırıcısı
Problem analizi
Naive Bayes Sınıflandırma programını Python kullanarak Makine Öğreniminde uygulamak için çok ünlü 'Iris Flower Dataset'i kullanacağız. Iris çiçeği veri seti veya Fisher's Iris veri seti, İngiliz istatistikçi, öjenist ve biyolog Ronald Fisher tarafından 1998'de tanıtılan çok değişkenli bir veri setidir. Bu, 3 sınıf hakkında bilgi içeren çok daha az sayısal veriden oluşan çok küçük ve temel bir veri setidir. Iris türüne ait çiçeklerden -
- iris setosa
- İris Versicolor
- iris virginica
Toplam 150 satırlık veri kümesine karşılık gelen üç türün her birinin 50 örneği vardır . Bu veri setinde kullanılan 4 öznitelik (veya) bağımsız değişken:
- çanak yaprağı uzunluğu cm
- çanak genişliği cm
- yaprak uzunluğu cm
- yaprak genişliği cm
Bağımlı değişken, yukarıda verilen dört nitelik ile tanımlanan çiçeğin “ tür ”üdür.
Adım 1 – Kitaplıkları İçe Aktarma
Her zaman olduğu gibi, herhangi bir Makine Öğrenimi modeli oluşturmanın birincil adımı, ilgili kitaplıkları içe aktarmak olacaktır. Bunun için verileri ön işleme için NumPy, Mathplotlib ve Pandas kitaplıklarını yükleyeceğiz.
numpy'yi np olarak içe aktar
matplotlib.pyplot'u plt olarak içe aktar
pandaları pd olarak içe aktar
Adım 2 – Veri Kümesini Yükleme
Naive Bayes Sınıflandırıcısını eğitmek için kullanılacak Iris çiçek veri seti, bir Pandas DataFrame'e yüklenecektir. 4 bağımsız değişken X değişkenine ve nihai çıktı türü değişkeni y'ye atanacaktır.
veri kümesi = pd.read_csv(' https://raw.githubusercontent.com/mk-gurucharan/Classification/master/IrisDataset.csv' )X = dataset.iloc[:,:4].values
y = veri kümesi['tür'].valuesdataset.head(5)>>
sepal_length sepal_width petal_length petal_width tür
5,1 3,5 1,4 0,2 setoza
4,9 3,0 1,4 0,2 setoza
4,7 3,2 1,3 0,2 setoza
4,6 3,1 1,5 0,2 setoza
5,0 3,6 1,4 0,2 setoza
Adım 3 – Veri setini Eğitim seti ve Test seti olarak bölme
Veri seti ve değişkenler yüklendikten sonra bir sonraki adım eğitim sürecinden geçecek değişkenlerin hazırlanmasıdır. Bu adımda, X ve y değişkenlerini eğitim ve test veri setlerine bölmemiz gerekiyor. Bunun için verilerin %80'ini rastgele olarak eğitim amaçlı kullanılacak eğitim setine, kalan %20'sini ise eğitilmiş Naive Bayes Sınıflandırıcısının doğruluğunun test edileceği test seti olarak atayacağız.
sklearn.model_selection'dan train_test_split'i içe aktarın
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
Adım 4 – Özellik Ölçeklendirme
Bu, bu küçük veri kümesine ek bir işlem olsa da, bunu daha büyük bir veri kümesinde kullanmanız için ekliyorum. Bunda, eğitim ve test setlerindeki veriler 0 ile 1 arasında bir değer aralığına küçültülür. Bu, hesaplama maliyetini düşürür.
sklearn.preprocessing'den içe aktarma StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
Adım 5 – Eğitim Setinde Naive Bayes Sınıflandırma modelinin eğitimi
Naive Bayes sınıfını sklearn kütüphanesinden içe aktarıyoruz. Bu model için Gauss modelini kullanıyoruz, Bernoulli, Kategorik ve Çok Terimli gibi birkaç model daha var. Böylece, X_train ve y_train, eğitim amacıyla sınıflandırıcı değişkene uyarlanır.
sklearn.naive_bayes'den GaussianNB'yi içe aktarın
sınıflandırıcı = GaussNB()
classifier.fit(X_tren, y_tren)
Adım 6 – Test seti sonuçlarını tahmin etme –
Eğitilen modeli kullanarak Test seti için türlerin sınıfını tahmin eder ve onu tür sınıfının Gerçek Değerleri ile karşılaştırırız.
y_pred = classifier.predict(X_test)
df = pd.DataFrame({'Gerçek Değerler':y_test, 'Öngörülen Değerler':y_pred})
df>>
Gerçek Değerler Öngörülen Değerler
setoza
setoza
virginica virginika
çok renkli çok renkli
setoza
setoza
……………
virginica versicolor
virginica virginika
setoza
setoza
çok renkli çok renkli
çok renkli çok renkli
Yukarıdaki karşılaştırmada virginica yerine Versicolor'u öngören bir yanlış tahmin olduğunu görüyoruz.
Adım 7 – Karışıklık Matrisi ve Doğruluk
Sınıflandırma ile uğraşırken, sınıflandırıcı modelimizi değerlendirmenin en iyi yolu, Karmaşa Matrisini doğruluğu ile birlikte test setine yazdırmaktır.
sklearn.metrics'den configuration_matrix'i içe aktarın
cm = sklearn.metrics içe aktarma doğruluğundan (y_test, y_pred) karışıklık_matrix(y_test, y_pred)

yazdır (“Doğruluk : “, doğruluk_skoru(y_test, y_pred))
cm>>Doğruluk : 0.9666666666666667
>>array([[14, 0, 0],
[ 0, 7, 0],
[ 0, 1, 8]])
Çözüm
Bu nedenle, bu makalede, Naive Bayes Algoritmasının temellerini inceledik, Elle çözülmüş bir örnekle birlikte Sınıflandırmanın arkasındaki matematiği anladık. Son olarak, Naive Bayes Sınıflandırma algoritmasını kullanarak popüler bir veri kümesini çözmek için bir Makine Öğrenimi kodu uyguladık.
Yapay zeka, makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, çalışan profesyoneller için tasarlanmış ve 450+ saatlik zorlu eğitim, 30'dan fazla vaka çalışması ve ödev sunan IIIT-B & upGrad'ın Makine Öğrenimi ve Yapay Zeka alanında PG Diplomasına göz atın. IIIT-B Mezun statüsü, 5+ pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.
Olasılık, Makine Öğreniminde nasıl yardımcı olur?
Gerçek dünya senaryolarında kısmi veya eksik bilgilere dayalı kararlar vermemiz gerekebilir. Olasılık, bu tür sistemlerdeki belirsizlikleri ölçmemize ve görev için riski yönetmemize yardımcı olur. Geleneksel yöntem yalnızca belirli eylemler için deterministik sonuçlar için çalışır, ancak herhangi bir tahmin modelinde her zaman bir miktar belirsizlik vardır. Bu belirsizlik, verilerdeki gürültü gibi giriş verilerinden gelen birçok parametreden gelebilir. Ayrıca, olasılık teoremlerinden bayesyen görünümler, girdi verilerinden örüntü tanımaya yardımcı olabilir. Bunun için olasılık, maksimum olabilirlik tahmin kavramını kullanır ve bu nedenle ilgili sonuçların üretilmesine yardımcı olur.
Karışıklık Matrisinin kullanımı nedir?
Karışıklık matrisi, sınıflandırma modelinin performansını yorumlamak için kullanılan 2x2'lik bir matristir. Bunun çalışması için girdi verilerinin gerçek değerlerinin bilinmesi gerekir, bu nedenle etiketlenmemiş veriler için temsil edilemez. Yanlış pozitiflerin (FP), gerçek pozitiflerin (TP), yanlış negatiflerin (FN) ve gerçek negatiflerin (TN) sayısından oluşur. Tahminler, eğitim setinden ve test setinden gelen sayım kullanılarak bu sınıflara sınıflandırılır. Doğruluk, kesinlik, hatırlama ve özgüllük gibi yararlı parametreleri görselleştirmemize yardımcı olur. Anlaması nispeten kolaydır ve size algoritma hakkında net bir fikir verir.
Naive Bayes modelinin farklı türleri nelerdir?
Tüm türler öncelikle Bayes Teoremine dayanmaktadır. Naive Bayes modelinin genel olarak üç türü vardır: Gaussian, Bernoulli ve Multinomial. Gaussian Naive Bayes, girdi parametrelerinden sürekli değerlere yardımcı olur ve tüm girdi verisi sınıflarının düzgün bir şekilde dağıldığı varsayımına sahiptir. Bernoulli'nin saf Bayes'i, veri özelliklerinin bağımsız olduğu ve boole değerlerinde bulunduğu olay tabanlı bir modeldir. Çok terimli Naive Bayes ayrıca olay tabanlı bir modele dayanmaktadır. Olayların oluşumuna bağlı olarak ilgili frekansları temsil eden vektör biçiminde veri özelliklerine sahiptir.
