Python'da Bilmeniz Gereken En Çok Kullanılan 7 Makine Öğrenimi Algoritması

Makine Öğrenimi, herhangi bir veri üzerinde kullanılan bilgisayar algoritmalarıyla ilgilenen Yapay Zekanın (AI) bir dalıdır. Beslenen verilerden otomatik olarak öğrenmeye odaklanır ve her seferinde önceki tahminleri geliştirerek bize sonuçlar verir.

Python'da Kullanılan En İyi Makine Öğrenimi Algoritmaları

Aşağıda, Python'da kullanılan en iyi makine öğrenimi algoritmalarından bazıları yer almaktadır ve kod parçacıkları, bunların sınıflandırma sınırlarının uygulanmasını ve görselleştirilmesini gösterir.

1. Doğrusal Regresyon

Doğrusal regresyon, en yaygın olarak kullanılan denetimli makine öğrenimi tekniklerinden biridir. Adından da anlaşılacağı gibi, bu regresyon doğrusal bir denklem kullanarak iki değişken arasındaki ilişkiyi modellemeye ve bu doğruyu gözlenen verilere uydurmaya çalışır. Bu teknik, yapılan toplam satışlar veya evlerin maliyeti gibi gerçek sürekli değerleri tahmin etmek için kullanılır.

En iyi uyum çizgisine regresyon çizgisi de denir. Aşağıdaki denklemle verilir:

Y = a*X + b

burada Y bağımlı değişken, a eğim, X bağımsız değişken ve b kesişme değeridir. a ve b katsayıları, çeşitli veri noktaları ve regresyon çizgisi denklemi arasındaki bu mesafe farkının karesini en aza indirerek türetilir.

# basit regresyon için sentetik veri seti

sklearn.datasets'ten make_regression dosyasını içe aktarın

plt.şekil()

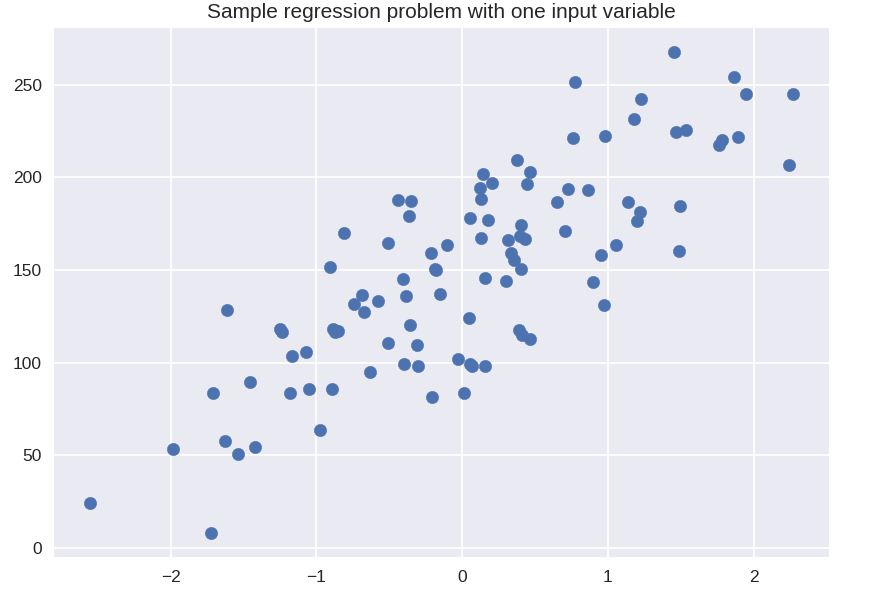
plt.title('Bir giriş değişkeni ile örnek regresyon problemi')

X_R1, y_R1 = make_regression( n_samples = 100, n_features = 1, n_informative = 1, bias = 150.0, noise = 30, random_state = 0 )

plt.scatter( X_R1, y_R1, işaretçi = 'o', s = 50 )

plt.göster()

sklearn.linear_model'den LinearRegression'ı içe aktarın

X_train, X_test, y_train, y_test = train_test_split( X_R1, y_R1,

rastgele_durum = 0 )

linreg = LinearRegression().fit( X_train, y_train )

print( 'doğrusal model katsayısı (w): {}'.format( linreg.coef_ ) )

print( 'doğrusal model kesişimi (b): {:.3f}'z.format( linreg.intercept_ ) )

print( 'R-kare puanı (eğitim): {:.3f}'.format( linreg.score( X_train, y_train ) ) )

print( 'R-kare puanı (test): {:.3f}'.format( linreg.score( X_test, y_test )) )

Çıktı

lineer model katsayısı (w): [ 45.71]

doğrusal model kesişimi (b): 148.446

R-kare puanı (eğitim): 0.679

R-kare puanı (test): 0.492

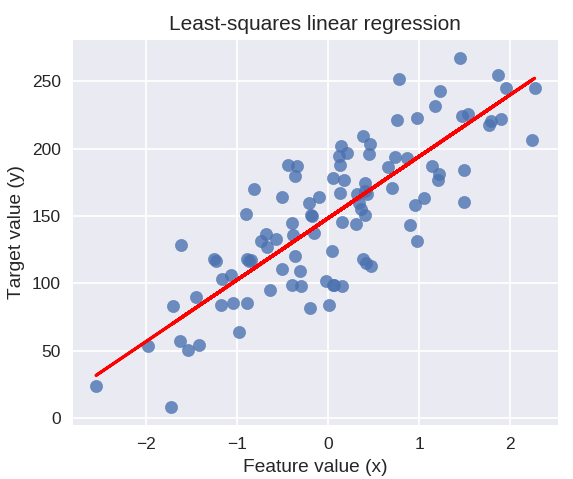
Aşağıdaki kod, veri noktalarımızın grafiğine uygun regresyon çizgisini çizecektir.

plt.figure( figsize = ( 5, 4 ) )

plt.scatter( X_R1, y_R1, işaretçi = 'o', s = 50, alfa = 0.8 )

plt.plot( X_R1, linreg.coef_ * X_R1 + linreg.intercept_, 'r-' )

plt.title( 'En küçük kareler doğrusal regresyon' )

plt.xlabel('Özellik değeri (x)')

plt.ylabel( 'Hedef değer (y)' )

plt.göster()

Sınıflandırma Tekniklerini Keşfetmek İçin Ortak Bir Veri Kümesi Hazırlama

Aşağıdaki veriler, Python'da makine öğreniminde en yaygın olarak kullanılan çeşitli sınıflandırma algoritmalarını göstermek için kullanılacaktır.

UCI Mantar Veri Kümesi , mantar.csv dosyasında saklanır.

%matplotlib not defteri

pandaları pd olarak içe aktar

numpy'yi np olarak içe aktar

matplotlib.pyplot'u plt olarak içe aktar

sklearn.decomposition'dan PCA'yı içe aktar

sklearn.model_selection'dan train_test_split'i içe aktarın

df = pd.read_csv( 'salt okunur/mantar.csv' )

df2 = pd.get_dummies(df)

df3 = df2.örnek( frak = 0.08)

X = df3.iloc[:, 2:]

y = df3.iloc[:, 1]

pca = PCA( n_components = 2 ).fit_transform( X )

X_train, X_test, y_train, y_test = train_test_split( pca, y, random_state = 0 )

plt.şekil( dpi = 120 )

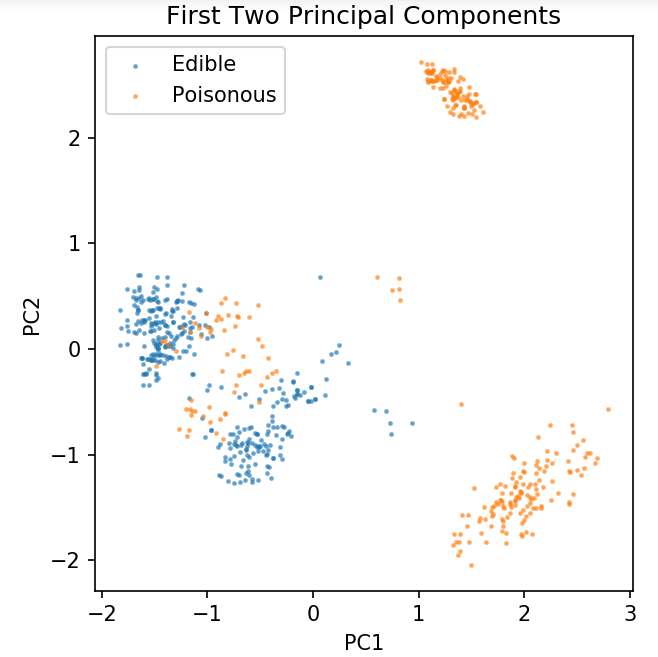
plt.scatter( pca[y.values ​​== 0, 0], pca[y.values ​​== 0, 1], alpha = 0.5, etiket = 'Yenilebilir', s = 2 )

plt.scatter( pca[y.values ​​== 1, 0], pca[y.values ​​== 1, 1], alpha = 0.5, label = 'Zehirli', s = 2 )

plt.legend()

plt.title( 'Mantar Veri Kümesi\nİlk İki Temel Bileşen')

plt.xlabel('PC1')

plt.ylabel('PC2')

plt.gca().set_aspect( 'eşit' )

Mantar veri setinde kullanacağımız farklı sınıflandırıcıların karar sınırlarını almak için aşağıda tanımlanan fonksiyonu kullanacağız.

def plot_mushroom_boundary( X, y, uygun_model ):

plt.figure( figsize = (9.8, 5), dpi = 100 )

i için, enumerate'de plot_type( ['Karar Sınırı', 'Karar Olasılıkları']):

plt.subplot( 1, 2, ben + 1 )

mesh_step_size = 0.01 # ağdaki adım boyutu

x_min, x_max = X[:, 0].min() – .1, X[:, 0].max() + .1

y_min, y_max = X[:, 1].min() – .1, X[:, 1].max() + .1

xx, yy = np.meshgrid( np.arange( x_min, x_max, mesh_step_size ), np.arange( y_min, y_max, mesh_step_size ) )

eğer ben == 0:

Z = fit_model.predict( np.c_[xx.ravel(), yy.ravel()] )

Başka:

denemek:

Z = fit_model.predict_proba( np.c_[xx.ravel(), yy.ravel()] )[:, 1]

hariç:

plt.text( 0.4, 0.5, 'Olasılıklar Kullanılamıyor', yatay hizalama = 'merkez', dikey hizalama = 'merkez', transform = plt.gca().transAxes, fontsize = 12 )

plt.axis('kapalı')

kırmak

Z = Z.yeniden şekil( xx.şekil )

plt.scatter( X[y.values ​​== 0, 0], X[y.values ​​== 0, 1], alpha = 0.4, label = 'Yenilebilir', s = 5)

plt.scatter( X[y.değerleri == 1, 0], X[y.değerleri == 1, 1], alfa = 0.4, etiket = 'Zehirli', s = 5)

plt.imshow( Z, enterpolasyon = 'en yakın', cmap = 'RdYlBu_r', alpha = 0.15, kapsam = ( x_min, x_max, y_min, y_max), orijin = 'düşük' )

plt.title( plot_type + '\n' + str( fit_model ).split( '(' )[0] + ' Test Doğruluğu: ' + str( np.round( fit_model.score( X, y ), 5 ) ) )

plt.gca().set_aspect('eşit');

plt.tight_layout()

plt.subplots_adjust( üst = 0.9, alt = 0.08, wspace = 0.02)

2. Lojistik Regresyon

Doğrusal regresyondan farklı olarak lojistik regresyon, ayrık değerlerin (0/1 ikili değerler, doğru/yanlış, evet/hayır) tahmini ile ilgilenir. Bu tekniğe logit regresyon da denir. Bunun nedeni, verilen verileri eğitmek için bir logit işlevi kullanarak bir olayın olasılığını tahmin etmesidir. Değeri her zaman 0 ile 1 arasındadır (çünkü bir olasılık hesaplamaktadır).

Sonuçların günlük oranları, tahmin değişkeninin doğrusal bir kombinasyonu olarak aşağıdaki gibi oluşturulur:

oranlar = p / (1 – p) = olayın olma olasılığı veya gerçekleşmeme olasılığı

ln( oranlar ) = ln( p / (1 – p))

logit( p ) = ln( p / (1 – p) ) = b0 + b1X1 + b2X2 + b3X3 + … + bkXk

p, bir özelliğin bulunma olasılığıdır.

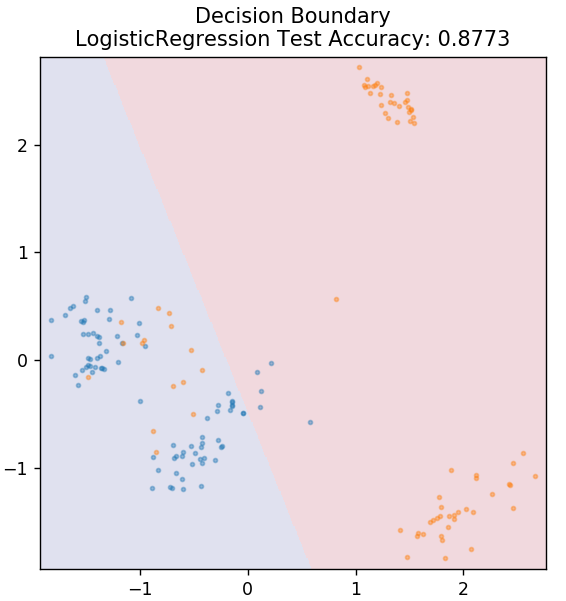
sklearn.linear_model'den LogisticRegression'ı içe aktarın

model = LojistikRegresyon()

model.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, model )

Kariyerinizi hızlandırmak için Dünyanın en iyi Üniversiteleri - Yüksek Lisanslar, Yönetici Yüksek Lisans Programları ve Makine Öğrenimi ve Yapay Zeka alanında İleri Düzey Sertifika Programından çevrimiçi olarak yapay zeka sertifikası alın .

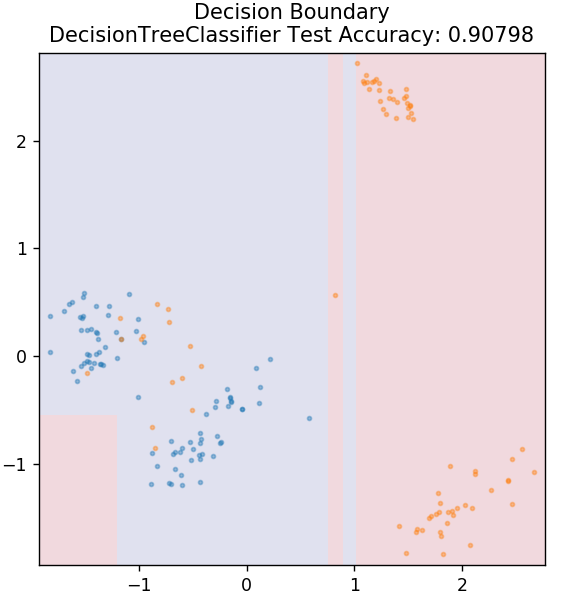
3. Karar Ağacı

Bu, hem sürekli hem de ayrık veri değişkenlerini sınıflandırmak için kullanılabilen çok popüler bir algoritmadır. Her adımda, veriler bazı ayırma özelliklerine/koşullarına dayalı olarak birden fazla homojen kümeye bölünür.

sklearn.tree'den DecisionTreeClassifier'ı içe aktarın

model = DecisionTreeClassifier( max_depth = 3 )

model.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, model )

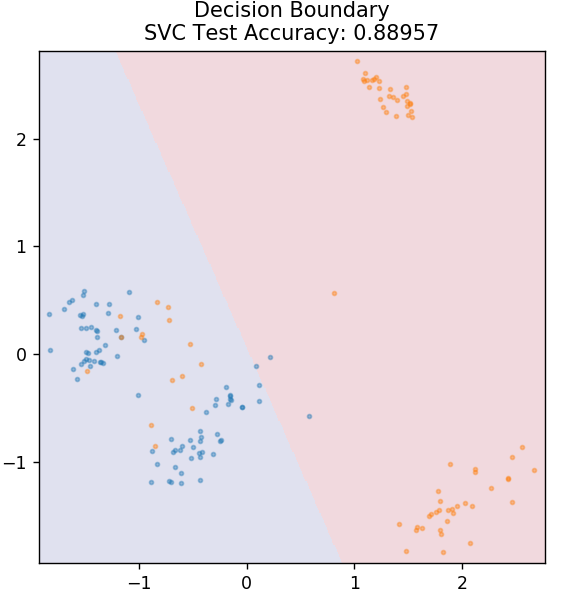
4. DVM

SVM, Support Vector Machines'in kısaltmasıdır. Buradaki temel fikir, ayırma için hiper düzlemler kullanarak veri noktalarını sınıflandırmaktır. Amaç, hem sınıfların hem de kategorilerin veri noktaları arasında maksimum mesafeye (veya kenar boşluğuna) sahip böyle bir hiperdüzlem bulmaktır.

Uçağı, gelecekte bilinmeyen noktaları en yüksek güvenle tasnif etmeye özen gösterecek şekilde seçiyoruz. SVM'ler, çok daha az hesaplama gücü alırken yüksek doğruluk sağladıkları için ünlüdür. DVM'ler regresyon problemleri için de kullanılabilir.

sklearn.svm'den SVC'yi içe aktar

model = SVC( çekirdek = 'doğrusal')

model.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, model )

Ödeme: GitHub'da Python Projeleri

5. Naif Bayes

Naive Bayes algoritması adından da anlaşılacağı gibi Bayes Teoremine dayalı denetimli bir öğrenme algoritmasıdır . Bayes Teoremi, verilen bazı bilgilere dayalı olarak size bir olayın olasılığını vermek için koşullu olasılıkları kullanır.

Neresi,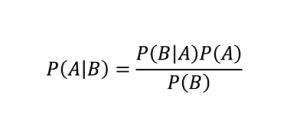

P (A | B): B olayının zaten gerçekleştiği göz önüne alındığında, A olayının gerçekleşmesinin koşullu olasılığı. (Arka olasılık da denir)

P(A): A olayının olasılığı.

P(B): B olayının olasılığı.

P (B | A): A olayının zaten gerçekleştiği göz önüne alındığında, B olayının gerçekleşmesinin koşullu olasılığı.

Bu algoritmanın adı neden Naive diye soruyorsunuz? Bunun nedeni, tüm olayların oluşumlarının birbirinden bağımsız olduğunu varsaymasıdır. Böylece her bir özellik, kendi aralarında herhangi bir bağımlılık olmaksızın, bir veri noktasının ait olduğu sınıfı ayrı ayrı tanımlar. Naive Bayes, metin kategorizasyonları için en iyi seçimdir. Küçük miktarlardaki eğitim verileriyle bile yeterince iyi çalışacaktır.

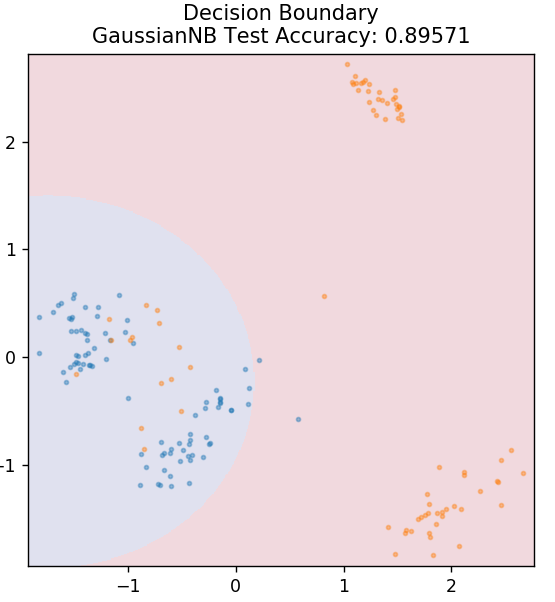
sklearn.naive_bayes'den GaussianNB'yi içe aktarın

model = GaussNB()

model.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, model )

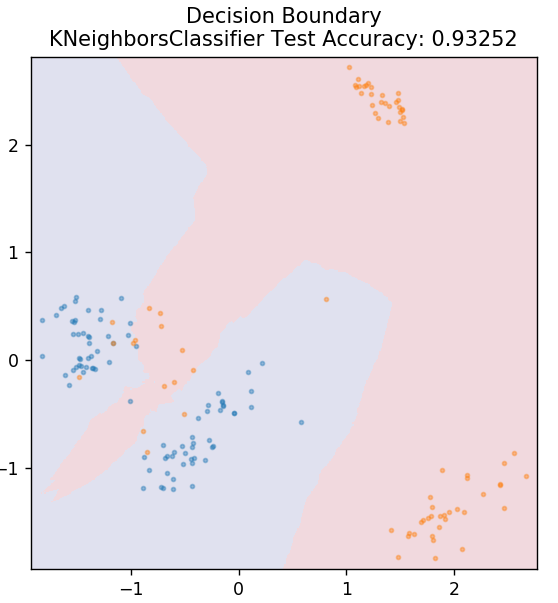
5. KNN

KNN, K-Nearest Neighbours anlamına gelir. Test verilerini daha önce sınıflandırılmış eğitim verileriyle benzerliklerine göre sınıflandıran çok yaygın kullanılan bir denetimli öğrenme algoritmasıdır. KNN, eğitim sırasında tüm veri noktalarını sınıflandırmaz. Bunun yerine, yalnızca veri kümesini depolar ve herhangi bir yeni veri aldığında, bu veri noktalarını benzerliklerine göre sınıflandırır. Bunu, o veri noktasının en yakın komşularının (burada, n_neighbors ) K sayısının Öklid mesafesini hesaplayarak yapar .

sklearn.neighbors'dan KNeighborsClassifier'ı içe aktarın

model = KNeighborsClassifier( n_neighbors = 20 )

model.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, model )

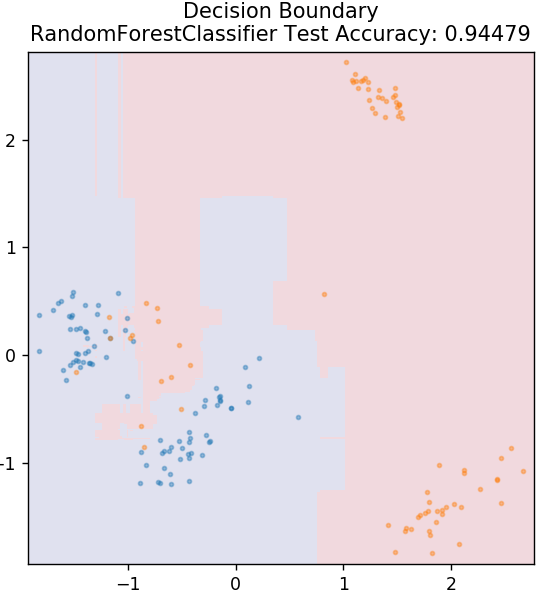
6. Rastgele Orman

Rastgele orman, denetimli bir öğrenme tekniği kullanan çok basit ve çeşitli bir makine öğrenme algoritmasıdır. Adından da tahmin edebileceğiniz gibi, rastgele orman, bir topluluk görevi gören çok sayıda karar ağacından oluşur. Her karar ağacı, veri noktalarının çıktı sınıfını belirleyecek ve çoğunluk sınıfı, modelin nihai çıktısı olarak seçilecektir. Buradaki fikir, aynı veriler üzerinde çalışan daha fazla ağacın, sonuçlarda tek tek ağaçlardan daha doğru olma eğiliminde olmasıdır.

sklearn.ensemble'dan RandomForestClassifier'ı içe aktarın

model = RandomForestClassifier()

model.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, model )

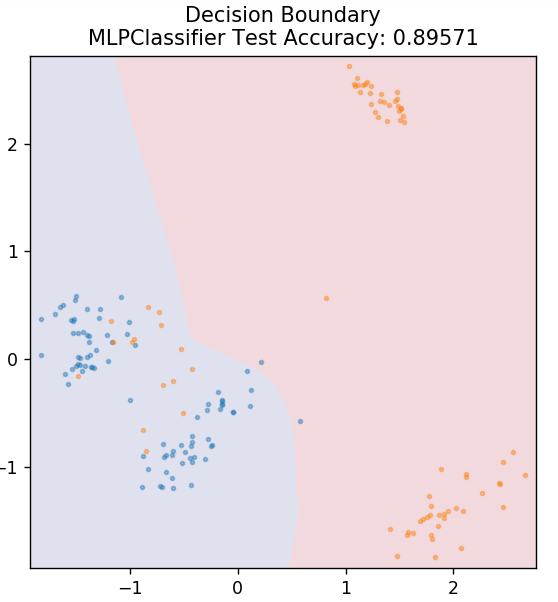
7. Çok Katmanlı Algılayıcı

Çok Katmanlı Algılayıcı (veya MLP), derin öğrenme dalı altına giren çok etkileyici bir algoritmadır. Daha spesifik olarak, ileri beslemeli yapay sinir ağları (YSA) sınıfına aittir. MLP, en az üç katmana sahip çoklu algılayıcılardan oluşan bir ağ oluşturur: bir girdi katmanı, çıktı katmanı ve gizli katman(lar). MLP'ler, doğrusal olarak ayrılamayan verileri ayırt edebilir.

Gizli katmanlardaki her nöron, bir sonraki katmana geçmek için bir aktivasyon işlevi kullanır. Burada, geri yayılım algoritması, parametreleri gerçekten ayarlamak ve dolayısıyla sinir ağını eğitmek için kullanılır. Çoğunlukla basit regresyon problemleri için kullanılabilir.

sklearn.neural_network'ten içe aktarma MLPClassifier

model = MLPClassifier()

model.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, model )

Ayrıca Okuyun: Python Proje Fikirleri ve Konuları

Çözüm

Farklı makine öğrenimi algoritmalarının farklı karar sınırları sağladığı ve dolayısıyla aynı veri setini sınıflandırmada farklı doğruluk sonuçları olduğu sonucuna varabiliriz.

Genel olarak her türlü veri için herhangi bir algoritmayı en iyi algoritma olarak ilan etmenin bir yolu yoktur. Makine öğrenimi, her bir veri kümesi için ayrı ayrı neyin en iyi sonucu verdiğini belirlemek için çeşitli algoritmalar için titiz deneme ve hatalar gerektirir. ML algoritmalarının listesi burada bitmiyor. Python'un Scikit-Learn kitaplığında keşfedilmeyi bekleyen çok sayıda başka teknik var. Devam edin ve tüm bunları kullanarak veri kümelerinizi eğitin ve eğlenin!

Karar ağaçları, makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, IIIT-B & upGrad'ın çalışan profesyoneller için tasarlanmış ve 450+ saatlik zorlu eğitim, 30'dan fazla vaka çalışması ve atamalar, IIIT-B Mezun statüsü, 5+ pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.