25 Makine Öğrenimi Mülakat Soruları ve Cevapları – Doğrusal Regresyon
Yayınlanan: 2022-09-08Veri bilimi adaylarını mülakatlarda yaygın olarak kullanılan makine öğrenimi algoritmaları üzerinde test etmek yaygın bir uygulamadır. Bu geleneksel algoritmalar lineer regresyon, lojistik regresyon, kümeleme, karar ağaçları vb.'dir. Veri bilimcilerinin bu algoritmalar hakkında derinlemesine bilgi sahibi olmaları beklenir.
Bir röportajda sordukları tipik ML soruları hakkında bilgi edinmek için çeşitli kuruluşlardan işe alım yöneticilerine ve veri bilimcilerine danıştık. Kapsamlı geri bildirimlerine dayanarak, veri bilimcilerin görüşmelerinde yardımcı olmak için bir dizi soru ve cevap hazırlandı. Doğrusal Regresyon görüşme soruları , Makine Öğrenimi görüşmelerinde en yaygın olanıdır. Bu algoritmalarla ilgili Soru-Cevap, dört blog gönderisinden oluşan bir dizi halinde sunulacaktır.
En İyi Makine Öğrenimi Kursları ve Çevrimiçi Yapay Zeka Kursları
| LJMU'dan Makine Öğrenimi ve Yapay Zeka Bilim Ustası | IIITB'den Makine Öğrenimi ve Yapay Zeka alanında Yönetici Yüksek Lisans Programı | |
| IIITB'den Makine Öğrenimi ve NLP'de İleri Düzey Sertifika Programı | IIITB'den Makine Öğrenimi ve Derin Öğrenmede Gelişmiş Sertifika Programı | Maryland Üniversitesi'nden Veri Bilimi ve Makine Öğrenimi alanında Yönetici Yüksek Lisans Programı |
| Tüm kurslarımızı keşfetmek için aşağıdaki sayfamızı ziyaret edin. | ||
| Makine Öğrenimi Kursları | ||
Her blog yazısı aşağıdaki konuyu kapsayacaktır: -
- Doğrusal Regresyon
- Lojistik regresyon
- kümeleme
- Tüm algoritmalara ait Karar Ağaçları ve Sorular
Doğrusal regresyonla başlayalım!
1. Doğrusal regresyon nedir?
Basit bir ifadeyle, doğrusal regresyon, verilen verilere uyan en iyi düz çizgiyi bulma yöntemidir, yani bağımsız ve bağımlı değişkenler arasındaki en iyi doğrusal ilişkiyi bulma.
Teknik terimlerle, doğrusal regresyon, herhangi bir veri üzerinde bağımsız ve bağımlı değişkenler arasında en iyi doğrusal-uyum ilişkisini bulan bir makine öğrenme algoritmasıdır. Çoğunlukla Kareli Artıkların Toplamı Yöntemi ile yapılır.
İsteğe Bağlı Makine Öğrenimi Becerileri
| Yapay Zeka Kursları | Tablo Kursları |
| NLP Kursları | Derin Öğrenme Kursları |

2. Doğrusal bir regresyon modelinde varsayımları belirtin.
Doğrusal bir regresyon modelinde üç ana varsayım vardır:
- Modelin formuyla ilgili varsayım:
Bağımlı ve bağımsız değişkenler arasında doğrusal bir ilişki olduğu varsayılmaktadır. 'Doğrusalite varsayımı' olarak bilinir. - Artıklarla ilgili varsayımlar:
- Normallik varsayımı: ε (i) hata terimlerinin normal dağıldığı varsayılır.
- Sıfır ortalama varsayımı: Kalıntıların ortalama değerinin sıfır olduğu varsayılır.
- Sabit varyans varsayımı: Artık terimlerin aynı (ancak bilinmeyen) varyansa sahip olduğu varsayılır, σ 2 Bu varsayım aynı zamanda homojenlik veya homoskedastisite varsayımı olarak da bilinir.
- Bağımsız hata varsayımı: Artık terimlerin birbirinden bağımsız olduğu varsayılır, yani ikili kovaryansları sıfırdır.
- Tahminciler hakkında varsayımlar:
- Bağımsız değişkenler hatasız ölçülür.
- Bağımsız değişkenler birbirinden lineer olarak bağımsızdır, yani verilerde çoklu bağlantı yoktur.
Açıklama:
- Bu kendi kendini açıklayıcı.
- Artıklar normal dağılmamışsa, rastgelelikleri kaybolur, bu da modelin verilerdeki ilişkiyi açıklayamadığı anlamına gelir.
Ayrıca, artıkların ortalaması sıfır olmalıdır.
Y (i)i = β 0 + β 1 x (i) + ε (i)
Bu, ε'nin artık terim olduğu varsayılan doğrusal modeldir.
E(Y) = E( β 0 + β 1 x (i) + ε (i) )
= E( β 0 + β 1 x (i) + ε (i) )
Artıkların beklentisi (ortalaması) E(ε (i) ), sıfır ise, modelin hedeflerinden biri olan hedef değişkenin ve modelin beklentileri aynı olur.
Artıklar (hata terimleri olarak da bilinir) bağımsız olmalıdır. Bu, artıklar ile tahmin edilen değerler arasında veya artıkların kendileri arasında bir korelasyon olmadığı anlamına gelir. Bir korelasyon varsa, regresyon modelinin tanımlayamadığı bir ilişki olduğu anlamına gelir. - Bağımsız değişkenler birbirinden lineer olarak bağımsız değilse, en küçük kareler çözümünün (veya normal denklem çözümünün) benzersizliği kaybolur.
Kariyerinizi hızlandırmak için Dünyanın en iyi Üniversiteleri - Yüksek Lisanslar, Yönetici Yüksek Lisans Programları ve Makine Öğrenimi ve Yapay Zeka alanında İleri Düzey Sertifika Programından çevrimiçi Yapay Zeka Kursuna katılın.
3. Özellik mühendisliği nedir? Modelleme sürecinde nasıl uyguluyorsunuz?
Özellik mühendisliği, ham verileri, temeldeki sorunu daha iyi temsil eden özelliklere, tahmine dayalı modellere dönüştürme sürecidir.
, görünmeyen veriler üzerinde geliştirilmiş model doğruluğu ile sonuçlanır.
Layman terimleriyle, özellik mühendisliği, sorunu daha iyi anlamanıza ve modellemenize yardımcı olabilecek yeni özelliklerin geliştirilmesi anlamına gelir. Özellik mühendisliği iki türdür - iş odaklı ve veri odaklı. İş odaklı özellik mühendisliği, iş açısından özelliklerin dahil edilmesi etrafında döner. Buradaki iş, iş değişkenlerini problemin özelliklerine dönüştürmektir. Veriye dayalı özellik mühendisliği durumunda, eklediğiniz özelliklerin önemli bir fiziksel yorumu yoktur, ancak hedef değişkenin tahmininde modele yardımcı olurlar.
Bilginize: Ücretsiz nlp kursu!
Özellik mühendisliğini uygulamak için veri kümesine tam olarak aşina olunmalıdır. Bu, verilen verinin ne olduğunu, neyi ifade ettiğini, ham özelliklerin neler olduğunu vb. bilmeyi içerir. Ayrıca, hedef değişkeni hangi faktörlerin etkilediği, değişkenin fiziksel yorumunun ne olduğu gibi problem hakkında net bir fikre sahip olmalısınız. , vb.
4. Düzenlileştirmenin kullanımı nedir? L1 ve L2 düzenlemelerini açıklayın.
Düzenlileştirme, modelin aşırı takılması sorununu çözmek için kullanılan bir tekniktir. Eğitim verileri üzerinde çok karmaşık bir model uygulandığında, fazla uyuyor. Bazen, basit model verileri genelleştiremeyebilir ve karmaşık model aşırıya kaçabilir. Bu sorunu çözmek için düzenlileştirme kullanılır.
Düzenleme, katsayı terimlerini (betalar) maliyet fonksiyonuna eklemekten başka bir şey değildir, böylece terimler cezalandırılır ve büyüklükleri küçüktür. Bu, esasen verilerdeki eğilimlerin yakalanmasına yardımcı olur ve aynı zamanda modelin çok karmaşık hale gelmesine izin vermeyerek fazla uydurmayı önler.
- L1 veya LASSO düzenlemesi: Burada katsayıların mutlak değerleri maliyet fonksiyonuna eklenir. Bu, aşağıdaki denklemde görülebilir; vurgulanan kısım L1 veya LASSO düzenlemesine karşılık gelir. Bu düzenlileştirme tekniği, öznitelik seçimine de yol açan seyrek sonuçlar verir.
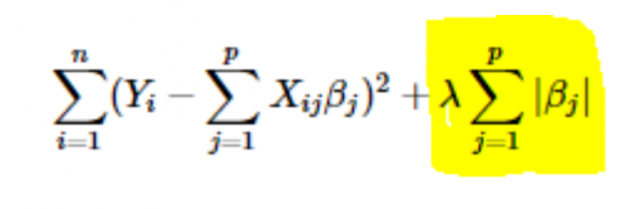
- L2 veya Ridge düzenlemesi: Burada katsayıların kareleri maliyet fonksiyonuna eklenir. Bu, vurgulanan kısmın L2 veya Ridge düzenlemesine karşılık geldiği aşağıdaki denklemde görülebilir.
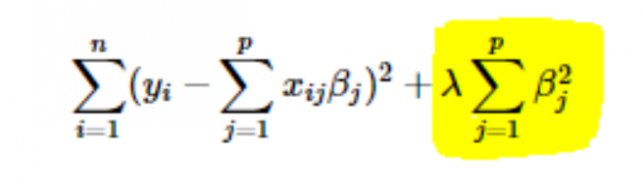
5. Parametre öğrenme oranı (α) değeri nasıl seçilir?
Öğrenme oranının değerini seçmek zor bir iştir. Değer çok küçükse, gradyan iniş algoritmasının optimal çözüme yakınsaması uzun zaman alır. Öte yandan, öğrenme hızının değeri yüksekse, gradyan inişi optimal çözümü aşacak ve büyük olasılıkla hiçbir zaman optimal çözüme yakınsamayacaktır.
Bu sorunun üstesinden gelmek için, bir dizi değer üzerinde farklı alfa değerleri deneyebilir ve maliyete karşı yineleme sayısı grafiğini çizebilirsiniz. Daha sonra grafiklere dayalı olarak hızlı düşüşü gösteren grafiğe karşılık gelen değer seçilebilir. 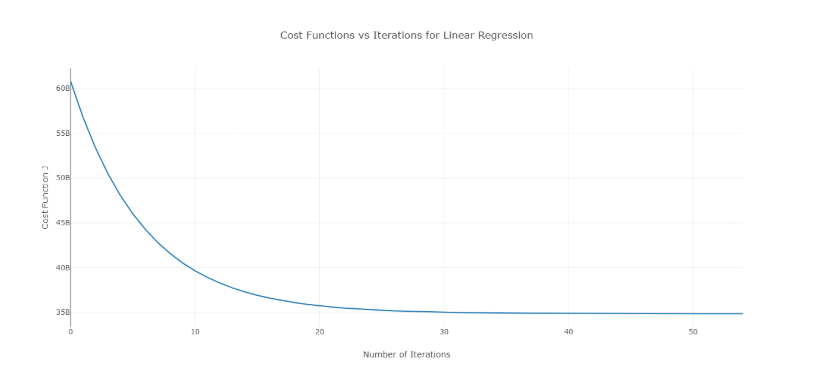
Yukarıda bahsedilen grafik, yineleme sayısı eğrisine karşı ideal bir maliyettir. Başlangıçta yineleme sayısı arttıkça maliyetin düştüğünü, ancak belirli yinelemelerden sonra gradyan inişinin yakınsadığını ve maliyetin artık düşmediğini unutmayın.
Eğer iterasyon sayısı arttıkça maliyetin arttığını görüyorsanız öğrenme oranı parametreniz yüksek ve düşürülmesi gerekiyor.
6. Düzenlileştirme parametresinin (λ) değeri nasıl seçilir?
Düzenlileştirme parametresini seçmek zor bir iştir. Eğer λ değeri çok yüksekse, regresyon katsayısının β son derece küçük değerlerine yol açacaktır , bu da modelin eksik kalmasına (yüksek sapma – düşük varyans) yol açacaktır. Öte yandan, λ değeri 0 (çok küçük) ise, model eğitim verisine fazla uyma eğiliminde olacaktır (düşük sapma – yüksek varyans).
λ değerini seçmenin uygun bir yolu yoktur . Yapabileceğiniz şey, bir veri alt örneğine sahip olmak ve algoritmayı farklı kümelerde birden çok kez çalıştırmaktır. Burada, kişi ne kadar varyansın tolere edilebileceğine karar vermelidir. Kullanıcı varyanstan memnun olduğunda, bu λ değeri tüm veri seti için seçilebilir.
Dikkat edilmesi gereken bir şey, burada seçilen λ değerinin tüm eğitim verileri için değil, o alt küme için optimal olduğudur.
7. Zaman serisi analizi için doğrusal regresyon kullanabilir miyiz?
Zaman serisi analizi için doğrusal regresyon kullanılabilir, ancak sonuçlar ümit verici değildir. Bu nedenle, genellikle bunu yapmak tavsiye edilmez. Bunun arkasındaki nedenler -
- Zaman serisi verileri çoğunlukla geleceğin tahmini için kullanılır, ancak doğrusal regresyon, ekstrapolasyon amaçlı olmadığı için nadiren gelecek tahmini için iyi sonuçlar verir.
- Çoğunlukla, zaman serisi verileri, en yoğun saatler, bayram mevsimleri vb. gibi, doğrusal regresyon analizinde büyük olasılıkla aykırı değerler olarak ele alınacak bir modele sahiptir.
8. Bir lineer regresyonun artıklarının toplamı hangi değere yakındır? Savunmak.
Ans Lineer regresyonun artıklarının toplamı 0'dır. Lineer regresyon, hataların (artıklar) normal olarak 0 ortalama ile dağıldığı varsayımıyla çalışır, yani
Y = β T X + ε
Burada Y, hedef veya bağımlı değişkendir,
β , regresyon katsayısının vektörüdür,
X, sütunlar olarak tüm özellikleri içeren özellik matrisidir,
ε, ε ~ N(0,σ 2 ) olacak şekilde artık terimdir .
Böylece, tüm artıkların toplamı, artıkların beklenen değeri çarpı toplam veri noktası sayısıdır. Artıkların beklentisi 0 olduğundan, tüm artık terimlerin toplamı sıfırdır.
Not : N(μ,σ 2 ), ortalama μ ve standart sapma σ 2 olan bir normal dağılım için standart gösterimdir .
9. Çoklu doğrusallık doğrusal regresyonu nasıl etkiler?
Ans Çoklu Bağlantılılık, bağımsız değişkenlerden bazıları birbirleriyle yüksek düzeyde (olumlu veya olumsuz) ilişkili olduğunda ortaya çıkar. Bu çoklu doğrusallık, doğrusal regresyonun temel varsayımına aykırı olduğu için bir soruna neden olur. Çoklu doğrusal bağlantının varlığı, modelin tahmin yeteneğini etkilemez. Bu nedenle, yalnızca tahminler istiyorsanız, çoklu bağlantının varlığı çıktınızı etkilemez. Ancak, modelden bazı içgörüler çıkarmak ve bunları diyelim ki bir iş modeline uygulamak isterseniz, sorunlara neden olabilir.
Çoklu bağlantının neden olduğu en büyük sorunlardan biri, yanlış yorumlara yol açması ve yanlış içgörüler sağlamasıdır. Doğrusal regresyon katsayıları, bir özellik bir birim değiştirilirse hedef değerdeki ortalama değişikliği gösterir. Dolayısıyla, eğer çoklu bağlantı varsa, bir özelliğin değiştirilmesi, ilişkili değişkende değişikliklere ve bunun sonucunda hedef değişkende değişikliklere yol açacağından, bu doğru değildir. Bu, yanlış içgörülere yol açar ve bir işletme için tehlikeli sonuçlar doğurabilir.
Çoklu bağlantı ile başa çıkmanın oldukça etkili bir yolu VIF (Varyans Enflasyon Faktörü) kullanmaktır. Bir özellik için VIF değeri ne kadar yüksekse, o özellik o kadar doğrusal olarak ilişkilidir. Çok yüksek VIF değerine sahip özelliği kaldırın ve modeli kalan veri kümesi üzerinde yeniden eğitin.
10. Doğrusal regresyonun normal formu (denklem) nedir? Gradyan iniş yöntemine ne zaman tercih edilmelidir?
Doğrusal regresyon için normal denklem -
β=(X T X) -1 . X TY
Burada Y=β T X lineer regresyon modelidir,
Y , hedef veya bağımlı değişkendir,
β , normal denklem kullanılarak ulaşılan regresyon katsayısının vektörüdür,
X , sütunlar olarak tüm özellikleri içeren özellik matrisidir.
Burada X matrisindeki ilk sütunun tüm 1'lerden oluştuğuna dikkat edin. Bu, regresyon çizgisi için ofset değerini dahil etmektir.
Gradyan iniş ve normal denklem arasındaki karşılaştırma:
| Dereceli alçalma | Normal Denklem |
| Alfa için hiper parametre ayarlaması gerekiyor (öğrenme parametresi) | Böyle bir ihtiyaç yok |
| yinelemeli bir süreçtir | Yinelemeli olmayan bir süreçtir |
| O(kn 2 ) zaman karmaşıklığı | O(n 3 ) X T X değerlendirmesi nedeniyle zaman karmaşıklığı |
| n son derece büyük olduğunda tercih edilir | n'nin büyük değerleri için oldukça yavaş olur |
Burada ' k ' eğim inişi için maksimum yineleme sayısıdır ve ' n ' eğitim setindeki toplam veri noktası sayısıdır.
Açıkça, büyük eğitim verilerimiz varsa, normal denklem kullanımı için tercih edilmez. Küçük ' n ' değerleri için, normal denklem gradyan inişinden daha hızlıdır.
Makine Öğrenimi Nedir ve Neden Önemlidir?
11. Regresyonunuzu verilerinizin farklı alt kümelerinde çalıştırırsınız ve her alt kümede belirli bir değişkenin beta değeri çılgınca değişir. Buradaki sorun ne olabilir?
Bu durum veri setinin heterojen olduğunu göstermektedir. Bu sorunun üstesinden gelebilmek için veri kümesinin farklı alt kümeler halinde kümelenmesi ve ardından her küme için ayrı modeller oluşturulması gerekir. Bu problemle başa çıkmanın bir başka yolu, heterojen verilerle oldukça verimli bir şekilde başa çıkabilen karar ağaçları gibi parametrik olmayan modelleri kullanmaktır.

12. Doğrusal regresyon çalışmaz ve regresyon katsayıları için sonsuz sayıda en iyi tahmin olduğunu bildirir. Ne yanlış olabilir?
Bu durum, bazı değişkenler arasında mükemmel bir korelasyon (pozitif veya negatif) olduğunda ortaya çıkar. Bu durumda katsayılar için benzersiz bir değer yoktur ve dolayısıyla verilen koşul ortaya çıkar.
13. Ayarlanmış R 2 ile ne demek istiyorsunuz ? R2'den farkı nedir ?
Düzeltilmiş R2 , tıpkı R2 gibi , regresyon çizgisinin etrafındaki noktaların bir temsilcisidir. Yani, modelin eğitim verilerine ne kadar iyi uyduğunu gösterir. Düzeltilmiş R 2 formülü dır-dir -
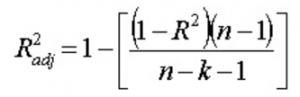
Burada n, veri noktalarının sayısıdır ve k, özelliklerin sayısıdır.
R 2'nin bir dezavantajı yeni özellik kullanışlı olsun ya da olmasın, her zaman yeni bir özelliğin eklenmesiyle artacak olmasıdır. Ayarlanmış R2 bu dezavantajı giderir. Ayarlanan R2 değeri ancak yeni eklenen özelliğin modelde önemli bir rol oynaması durumunda artar.
14. Artık değere karşı uygun değer eğrisini nasıl yorumluyorsunuz?
Artık değere karşı uygun değer grafiği, tahmin edilen değerlerin ve artıkların bir korelasyona sahip olup olmadığını görmek için kullanılır. Artıklar, uygun değer etrafında bir ortalama ve sabit bir varyans ile normal olarak dağılırsa, modelimiz iyi çalışıyor; Aksi takdirde, modelle ilgili bir sorun vardır.
Modeli geniş bir veri kümesi aralığında eğitirken bulunabilecek en yaygın sorun değişen varyanstır (bu, aşağıdaki yanıtta açıklanmıştır). Değişen varyansın varlığı, artık değere karşı uygun değer eğrisi çizilerek kolayca görülebilir.
15. Değişen varyans nedir? Sonuçları nelerdir ve bunun üstesinden nasıl gelebilirsiniz?
Farklı alt popülasyonlar farklı değişkenlere sahip olduğunda (standart sapma) rastgele bir değişkenin değişen varyanslı olduğu söylenir.
Değişen varyansın varlığı, varsayımın hata terimlerinin ilişkisiz olduğunu ve dolayısıyla varyansın sabit olduğunu söylediği için regresyon analizinde belirli sorunlara yol açar. Değişen varyansın varlığı, genellikle artık değerlere karşı sabit değerler için koni benzeri bir dağılım grafiği şeklinde görülebilir.
Doğrusal regresyonun temel varsayımlarından biri, verilerde değişen varyans olmamasıdır. Varsayımların ihlali nedeniyle, Sıradan En Küçük Kareler (OLS) tahmin edicileri, En İyi Doğrusal Tarafsız Tahminciler (BLUE) değildir. Bu nedenle, diğer Doğrusal Yansız Tahmin Edicilerden (LUE'ler) en az varyansı vermezler.
Değişen varyansın üstesinden gelmek için sabit bir prosedür yoktur. Bununla birlikte, değişen varyansın azalmasına yol açabilecek bazı yollar vardır. Bunlar -
- Verilerin logaritması: Üstel olarak artan bir seri, genellikle artan değişkenlik ile sonuçlanır. Bu, log dönüşümü kullanılarak aşılabilir.
- Ağırlıklı doğrusal regresyon kullanma: Burada, X ve Y'nin ağırlıklı değerlerine OLS yöntemi uygulanır. Bir yol, doğrudan bağımlı değişkenin büyüklüğü ile ilgili ağırlıkları eklemektir.
16. VIF nedir? Nasıl hesaplarsın?
Varyans Enflasyon Faktörü (VIF), bir veri setinde çoklu bağlantının varlığını kontrol etmek için kullanılır. Şu şekilde hesaplanır:
Burada, VIF j , j'inci değişken için VIF'nin değeridir ,
R j 2 o değişkenin diğer tüm bağımsız değişkenlere karşı regresyonu yapıldığında modelin R2 değeridir.
Bir değişken için VIF değeri yüksekse, R 2 karşılık gelen modelin değeri yüksektir, yani diğer bağımsız değişkenler o değişkeni açıklayabilir. Basit bir ifadeyle, değişken diğer bazı değişkenlere doğrusal olarak bağımlıdır.
17. Herhangi bir veri için lineer regresyonun uygun olduğunu nereden biliyorsunuz?
Herhangi bir veri için doğrusal regresyonun uygun olup olmadığını görmek için bir dağılım grafiği kullanılabilir. İlişki doğrusal görünüyorsa, doğrusal bir modele gidebiliriz. Ancak durum böyle değilse, ilişkiyi lineer hale getirmek için bazı dönüşümler uygulamamız gerekir. Basit veya tek değişkenli doğrusal regresyon durumunda dağılım grafiklerini çizmek kolaydır. Ancak çok değişkenli doğrusal regresyon durumunda, iki boyutlu ikili dağılım grafikleri, dönen grafikler ve dinamik grafikler çizilebilir.
18. Doğrusal regresyonda hipotez testi nasıl kullanılır?
Hipotez testi, aşağıdaki amaçlar için doğrusal regresyonda gerçekleştirilebilir:
- Hedef değişkenin tahmini için bir tahmin edicinin anlamlı olup olmadığını kontrol etmek. Bunun için iki yaygın yöntem -
- p değerlerinin kullanılmasıyla:
Bir değişkenin p değeri belirli bir sınırdan (genellikle 0.05) büyükse, değişken hedef değişkenin tahmininde önemsizdir. - Regresyon katsayısının değerlerini kontrol ederek:
Bir tahmin ediciye karşılık gelen regresyon katsayısının değeri sıfır ise, bu değişken hedef değişkenin tahmininde önemsizdir ve onunla doğrusal bir ilişkisi yoktur.
- p değerlerinin kullanılmasıyla:
- Hesaplanan regresyon katsayılarının gerçek katsayıların iyi tahmin edicileri olup olmadığını kontrol etmek.
19. Gradyan inişini lineer regresyona göre açıklayın.
Gradyan iniş bir optimizasyon algoritmasıdır. Doğrusal regresyonda, maliyet fonksiyonunu optimize etmek ve maliyet fonksiyonunun optimize edilmiş değerine karşılık gelen βs (tahmin ediciler) değerlerini bulmak için kullanılır.
Gradyan inişi, grafiği aşağı yuvarlayan bir top gibi çalışır (atalet yok sayılarak). Top, en büyük eğim yönü boyunca hareket eder ve düz yüzeyde (minima) durur. 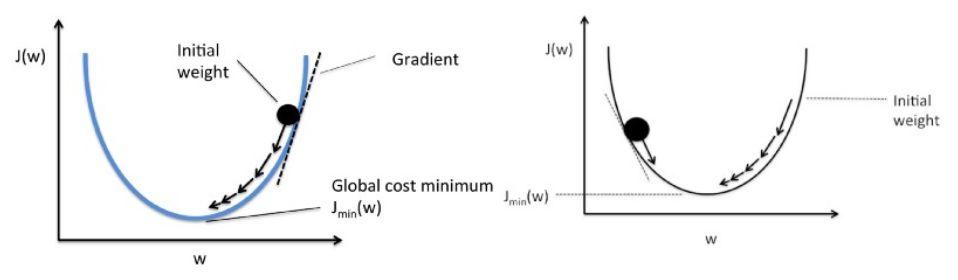
Matematiksel olarak, lineer regresyon için gradyan inişinin amacı aşağıdakilerin çözümünü bulmaktır.
ArgMin J(Θ 0 ,Θ 1 ), burada J(Θ 0 ,Θ 1 ) doğrusal regresyonun maliyet fonksiyonudur. tarafından verilir - 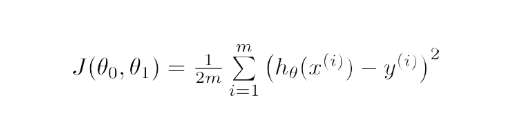
Burada h lineer hipotez modelidir, h=Θ 0 + Θ 1 x, y gerçek çıktıdır ve m , eğitim kümesindeki veri noktalarının sayısıdır.
Gradient Descent rastgele bir çözümle başlar ve daha sonra degradenin yönüne bağlı olarak çözüm, maliyet fonksiyonunun daha düşük bir değere sahip olduğu yeni değere güncellenir.
Güncelleme:
yakınsama kadar tekrarlayın 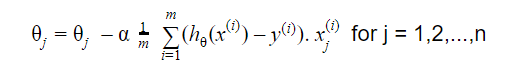
20. Doğrusal bir regresyon modelini nasıl yorumlarsınız?
Doğrusal bir regresyon modelinin yorumlanması oldukça kolaydır. Model aşağıdaki formdadır: 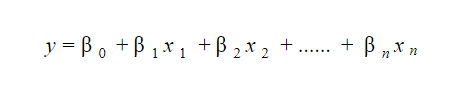
Bu modelin önemi, marjinal değişiklikleri ve bunların sonuçlarını kolayca yorumlayıp anlayabilmenizde yatmaktadır. Örneğin, diğer değişkenler sabit tutularak x 0 değeri 1 birim artarsa, y değerindeki toplam artış β i olacaktır . Matematiksel olarak, kesme terimi ( β 0 ), tüm öngörücü terimler sıfıra ayarlandığında veya dikkate alınmadığında verilen yanıttır.
Bu 6 Makine Öğrenimi Tekniği Sağlık Hizmetlerini İyileştiriyor
21. Güçlü regresyon nedir?
Bir regresyon modeli doğası gereği sağlam olmalıdır. Bu, birkaç gözlemdeki değişikliklerle modelin büyük ölçüde değişmemesi gerektiği anlamına gelir. Ayrıca aykırı değerlerden fazla etkilenmemelidir.
OLS (Olağan En Küçük Kareler) içeren bir regresyon modeli, aykırı değerlere karşı oldukça hassastır. Bu sorunun üstesinden gelmek için, regresyon katsayılarının tahmin edicilerini belirlemek için WLS (Ağırlıklı En Küçük Kareler) yöntemini kullanabiliriz. Burada, uç değerlere daha az ağırlık verilir veya bağlantıdaki yüksek kaldıraç noktaları, bu noktaların daha az etkili olmasını sağlar.
22. Model uydurmadan önce hangi grafiklerin izlenmesi önerilir?
Modeli yerleştirmeden önce, değişkenlerdeki trendler, dağılım, çarpıklık vb. gibi verilerin iyi bilinmesi gerekir. Değişkenlerin dağılımını gözlemlemek için histogramlar, kutu çizimleri ve nokta çizimleri gibi grafikler kullanılabilir. Bunun dışında bağımlı ve bağımsız değişkenler arasındaki ilişkinin ne olduğu da analiz edilmelidir. Bu, dağılım grafikleri (tek değişkenli problemler olması durumunda), dönen grafikler, dinamik grafikler vb. ile yapılabilir.
23. Genelleştirilmiş doğrusal model nedir?
Genelleştirilmiş doğrusal model, sıradan doğrusal regresyon modelinin türevidir. GLM, artıklar açısından daha esnektir ve doğrusal regresyonun uygun görünmediği durumlarda kullanılabilir. GLM, artıkların dağılımının normal dağılımdan farklı olmasına izin verir. Doğrusal modelin bağlantı işlevini kullanarak hedef değişkene bağlanmasına izin vererek doğrusal regresyonu genelleştirir. Model tahmini, maksimum olabilirlik tahmini yöntemi kullanılarak yapılır.
24. Önyargı-varyans değiş tokuşunu açıklayın.
Sapma, model tarafından tahmin edilen değerler ile gerçek değerler arasındaki farkı ifade eder. Bu bir hatadır. Bir ML algoritmasının hedeflerinden biri, düşük bir önyargıya sahip olmaktır.
Varyans, modelin eğitim veri setindeki küçük dalgalanmalara duyarlılığını ifade eder. Bir ML algoritmasının diğer bir amacı, düşük varyansa sahip olmaktır.
Tam olarak doğrusal olmayan bir veri kümesi için aynı anda hem yanlılığın hem de varyansın düşük olması mümkün değildir. Düz çizgi modeli düşük varyansa sahip ancak yüksek sapmaya sahip olurken, yüksek dereceli bir polinom düşük sapmalı ancak yüksek varyansa sahip olacaktır.
Makine öğreniminde önyargı ve varyans arasındaki ilişkiden kaçış yoktur.
- Önyargıyı azaltmak varyansı artırır.
- Varyansı azaltmak yanlılığı artırır.
Yani, ikisi arasında bir değiş tokuş var; Makine öğrenimi uzmanı, atanan soruna bağlı olarak, ne kadar yanlılık ve varyansın tolere edilebileceğine karar vermelidir. Buna dayanarak, nihai model inşa edilmiştir.
25. Öğrenme eğrileri daha iyi bir model oluşturmaya nasıl yardımcı olabilir?
Öğrenme eğrileri, fazla ya da eksik uyumun varlığının göstergesini verir.
Bir öğrenme eğrisinde, eğitim hatası ve çapraz doğrulama hatası, eğitim veri noktalarının sayısına karşı çizilir. Tipik bir öğrenme eğrisi şöyle görünür: 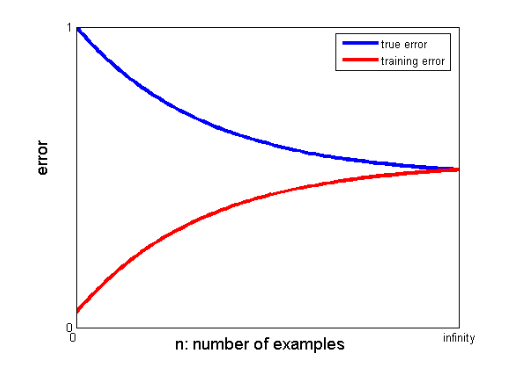
Eğitim hatası ve gerçek hata (çapraz doğrulama hatası) aynı değere yakınsarsa ve hatanın karşılık gelen değeri yüksekse, bu modelin uyumsuz olduğunu ve yüksek önyargıdan muzdarip olduğunu gösterir.
Makine Öğrenimi Röportajları ve Nasıl Başarılı Olunur?
Makine Öğrenimi Mülakatları türlere veya kategorilere göre değişiklik gösterebilir, örneğin birkaç işe alım uzmanı birçok Lineer Regresyon mülakat sorusu sorar . Makine Öğrenimi Mühendisi mülakatı rolüne giderken Kodlama, Araştırma, Vaka Çalışması, Proje Yönetimi, Sunum, Sistem Tasarımı ve İstatistik gibi kategorilerde uzmanlaşabilirler. En yaygın kategori türlerine ve bunlara nasıl hazırlanılacağına odaklanacağız.
- kodlama
Kodlama ve programlama, bir makine öğrenimi görüşmesinin önemli bileşenleridir ve başvuranları taramak için sıklıkla kullanılır. Bu röportajlarda başarılı olmak için sağlam programlama becerilerine sahip olmanız gerekir. Kodlama görüşmeleri genellikle 45 ila 60 dakika sürer ve yalnızca iki sorudan oluşur. Görüşmeci konuyu ortaya koyar ve başvuranın mümkün olan en kısa sürede ele alacağını tahmin eder.
Nasıl hazırlanır – Veri yapılarını, zaman ve mekanın karmaşıklığını, yönetim becerilerini ve bir sorunu anlama ve çözme becerisini iyi anlayarak bu görüşmelere hazırlanabilirsiniz. upGrad , kodlama becerilerinizi geliştirmenize ve bu röportajda başarılı olmanıza yardımcı olabilecek harika bir yazılım mühendisliği kursuna sahiptir.
2. Makine Öğrenimi
Makine öğrenimi anlayışınız, görüşmeler yoluyla değerlendirilecektir. Konvolüsyonel katmanlar, tekrarlayan sinir ağları, üretken düşman ağları, konuşma tanıma ve diğer konular, istihdam ihtiyaçlarına bağlı olarak kapsanabilir.
Nasıl hazırlanır – Bu görüşmede başarılı olabilmek için, iş rollerini ve sorumluluklarını tam olarak anladığınızdan emin olmalısınız. Bu, incelemeniz gereken makine öğreniminin özelliklerini belirlemenize yardımcı olacaktır. Ancak, herhangi bir spesifikasyonla karşılaşmazsanız, temelleri derinlemesine anlamalısınız. upGrad'ın sağladığı kapsamlı bir makine öğrenimi kursu bu konuda size yardımcı olabilir. Ayrıca, en son trendlerini anlamak için ML ve AI ile ilgili en son makaleleri inceleyebilir ve bunları düzenli olarak dahil edebilirsiniz.
3. Tarama
Bu görüşme biraz gayri resmidir ve tipik olarak görüşmenin ilk noktalarından biridir. Potansiyel bir işveren genellikle bunu halleder. Bu görüşmenin ana amacı, başvuru sahibine iş, rol ve görevler hakkında bir fikir vermektir. Daha resmi olmayan bir ortamda, adayın ilgi alanlarının pozisyonla eşleşip eşleşmediğini belirlemek için geçmişleri hakkında da sorgulanır.
Nasıl hazırlanır - Bu, röportajın çok teknik olmayan bir parçasıdır. Tüm bunlar, dürüstlüğünüz ve Makine Öğrenimi konusundaki uzmanlığınızın temelleridir.
4. Sistem Tasarımı
Bu tür görüşmeler, bir kişinin baştan sona tamamen ölçeklenebilir bir çözüm yaratma kapasitesini test eder. Mühendislerin çoğu bir konuyla o kadar meşguller ki, çoğu zaman daha geniş resmi gözden kaçırıyorlar. Bir sistem tasarımı görüşmesi, bir çözüm üretmek için bir araya gelen çok sayıda unsurun anlaşılmasını gerektirir. Bu öğeler, ön uç düzenini, yük dengeleyiciyi, önbelleği ve daha fazlasını içerir. Bu konular iyi anlaşıldığında, etkili ve ölçeklenebilir bir uçtan uca sistem geliştirmek daha kolaydır.
Nasıl hazırlanır – Sistem tasarım projesinin kavramlarını ve bileşenlerini anlayın. Projeyi daha iyi anlamak için görüşmecinize yapıyı açıklamak için gerçek hayattan örnekler kullanın.
Popüler Makine Öğrenimi ve Yapay Zeka Blogları
| IoT: Tarih, Bugün ve Gelecek | Makine Öğrenimi Eğitimi: Makine Öğrenimi Öğrenin | Algoritma nedir? Basit ve Kolay |
| Hindistan'da Robotik Mühendisi Maaşı : Tüm Roller | Bir Makine Öğrenimi Mühendisinin Hayatından Bir Gün: Ne yapıyorlar? | IoT (Nesnelerin İnterneti) Nedir? |
| Permütasyon ve Kombinasyon: Permütasyon ve Kombinasyon Arasındaki Fark | Yapay Zeka ve Makine Öğreniminde En İyi 7 Trend | R ile Makine Öğrenimi: Bilmeniz Gereken Her Şey |

Eğitimin yakınsak değerleri ile çapraz doğrulama hataları arasında önemli bir boşluk varsa, yani çapraz doğrulama hatası eğitim hatasından önemli ölçüde yüksekse, bu modelin eğitim verilerine fazla uyduğunu ve yüksek varyanstan muzdarip olduğunu gösterir. .
Makine Öğrenimi Mühendisleri: Mitler ve Gerçekler
Bu serinin ilk bölümünün sonu. Serinin Lojistik Regresyona dayalı sorulardan oluşan bir sonraki bölümü için bekleyin . Yorumlarınızı göndermekten çekinmeyin.
Ortak yazar – Ojas Agarwal
Pratik uygulamalı atölyeler, bire bir sektör danışmanı, 12 vaka çalışması ve ödev, IIIT-B Mezunu statüsü ve daha fazlasını sağlayan Makine Öğrenimi ve Yapay Zeka'daki Yönetici PG Programımızı inceleyebilirsiniz.
Düzenlemeden ne anlıyorsunuz?
Düzenlileştirme, modele aşırı uyum sorunuyla başa çıkmak için bir stratejidir. Aşırı uyum, eğitim verilerine karmaşık bir model uygulandığında meydana gelir. Temel model zaman zaman verileri genelleştiremeyebilir ve karmaşık model verilere fazla sığabilir. Bu sorunu hafifletmek için düzenleme kullanılır. Düzenlileştirme, terimleri cezalandıracak ve mütevazı bir büyüklüğe sahip olacak şekilde minimizasyon problemine katsayı terimleri (betalar) ekleme işlemidir. Bu, esas olarak, modelin çok karmaşık hale gelmesini önleyerek fazla uydurmayı önlerken veri modellerini tanımlamaya yardımcı olur.
Özellik mühendisliği hakkında ne anlıyorsunuz?
Özgün verileri, altta yatan sorunu daha iyi tanımlayan özelliklere dönüştürme süreci, öngörülebilir modellere dönüştürülerek, görünmeyen veriler üzerinde gelişmiş model doğruluğu ile sonuçlanır, özellik mühendisliği olarak bilinir. Layman'ın terimleriyle, özellik mühendisliği, bir konunun daha iyi anlaşılmasına ve modellenmesine yardımcı olabilecek ek özelliklerin yaratılması anlamına gelir. İki tür özellik mühendisliği vardır: iş odaklı ve veri odaklı. Ticari bir bakış açısından özelliklerin dahil edilmesi, iş odaklı özellik mühendisliğinin odak noktasıdır.
Önyargı-varyans değiş tokuşu nedir?
Model - tahmin edilen değerler ile gerçek değerler arasındaki boşluk, sapma olarak adlandırılır. Bu bir hata. Düşük bir önyargı, bir ML algoritmasının hedeflerinden biridir. Modelin eğitim veri kümesindeki küçük değişikliklere karşı savunmasızlığına varyans denir. Düşük varyans, bir ML algoritmasının başka bir amacıdır. Mükemmel doğrusal olmayan bir veri kümesinde hem düşük yanlılığa hem de düşük varyansa sahip olmak imkansızdır. Düz çizgi modelinin varyansı düşüktür, ancak sapma büyüktür, yüksek dereceli bir polinomun varyansı düşüktür, ancak sapma yüksektir. Makine öğreniminde, önyargı ve varyasyon arasındaki bağlantı kaçınılmazdır.
