Olasılık Yoğunluk Fonksiyonuna Giriş [Formül, Özellikler, Uygulamalar, Örnekler]

Olasılık Yoğunluk Fonksiyonu (PDF), istatistikte kesikli bir rastgele değişkenin olasılık dağılımını gösteren bir ifadedir. Olasılık dağılımı, basit bir ifadeyle, hisse senedi veya ETF gibi rastgele bir değişkenin sonucunun olasılığı olarak tanımlanabilir. Kesin değeri belirlenebilen sürekli bir rastgele değişkenin aksine ayrık değişkenler ortaya çıkar.

Örneğin, bir borsadaki komut dosyasının değeri, herhangi bir sayıda ondalık basamaklı sürekli bir değişken yerine ayrı bir rastgele değişkende yalnızca iki ondalık basamağa (örneğin, 65.76) sahiptir (örnek: 65.7685434567).

Olasılık yoğunluk işlevi, kesikli bir rastgele değişkenin sonucunun olasılığını belirlemek için kullanılan istatistiksel bir araçtır. PDF'ler bir grafik üzerinde çizildiğinde, eğrinin altındaki alanın sonucun olasılığını temsil ettiği bir çan eğrisine benzer görünür.

Bir grafik model olarak yansıtıldığında, eğrinin altındaki alan, ayrık rasgele değişkenlerin değerlerinin düşeceği aralığı temsil eder. Böylece, eğrinin altındaki toplam alan, değişkenin sonucunun olasılığına eşittir.

Olasılık yoğunluğu işlevi, belirli bir değer aralığına düşen rastgele bir değişkenin olasılığını belirleyebilir.

Tipik olarak, olasılık yoğunluğu işlevleri, borsadaki belirli bir fonla ilişkili riskleri ve potansiyel geliri analiz eder.

Olasılık Yoğunluk Fonksiyonu olarak kabul edilecek bir fonksiyon tarafından sağlanacak koşullar

Kesintisiz bir değişkenin değeri, sonsuz sayıda değere sahip olabilen sürekli bir değişkenin aksine doğru bir şekilde ölçülebilir. Herhangi bir fonksiyonun olasılık yoğunluk fonksiyonu olabilmesi için aşağıdaki iki koşulu sağlaması gerekir:

• Rastgele değişkenin her olası değeri için f(x) değeri pozitif (negatif olmayan) olmalıdır.
• Eğrinin toplam alanının integral değeri (rastgele değişkenin tüm olası değerlerinin integrali) 1 olmalıdır.

Olasılık Yoğunluk Fonksiyonu ile Olasılık Dağılım Fonksiyonu Arasındaki Fark

Rastgele değişkenler birçok değere sahip olabilir. Rastgele bir değişkenin sahip olabileceği her olası değerin tanımına olasılık dağılımı denir.

Olasılık dağılımı, bir dizi sonuç ve bunlarla ilgili olasılıkları verir. Sürekli bir olasılık dağılımını temsil eden istatistiksel fonksiyon, olasılık yoğunluk fonksiyonu olarak bilinir.

Olasılık kütle fonksiyonu adı verilen ayrı bir olasılık dağılımını temsil eden başka bir istatistiksel araç vardır. Bu, tüm olası sonuçların ve olasılık olasılıklarının ayrıntılı bir hesabını verir.

Olasılık Yoğunluk Fonksiyonları İçin İfade

Rastgele değişken kesikli ise olasılık dağılımına olasılık kütle fonksiyonu, sürekli değişken ise olasılık dağılımına olasılık yoğunluk fonksiyonu denir.

Söz konusu rastgele değişken bir dizi olası değere sahip olduğunda bir PDF kullanılır. Olasılık dağılımları, kesin değeri belirlemek için kullanılır.

Rastgele değişken X ile gösterilsin. X rastgele değişkeninin olasılık yoğunluk fonksiyonu, f şu şekilde ifade edilebilir.

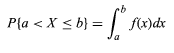
• Rastgele değişkenin değeri a ve b arasındadır.
• X, r ve s aralığından (aralık) belirli bir sayı seçme olasılığını gösteriyorsa, olasılık yoğunluk fonksiyonu şu şekilde ifade edilebilir:

r < x < s için f ( x ) = 1/( s - r ) ve x < r veya x > s için f ( x ) = 0 .

• PDF F şu şekilde temsil edilir:

F ( x ) = P { X ≤ x }

buna X'in dağılım işlevi veya kümülatif dağılım işlevi denir.

Rastgele değişken X'in bir olasılık dağılım fonksiyonu f ( x ) olduğu göz önüne alındığında, f ve F arasındaki ilişki şu şekilde kurulabilir:

F ′(. x ) = f ( x )

Kesikli bir rastgele değişkenin dağılım işlevi, olasılık dağılım işlevinden farklıdır. İkisi arasındaki ilişki aşağıdaki gibi ifade edilebilir:

Rastgele değişkenin beklentisi şu şekilde gösterilir:

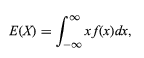
Böylece, tüm ayrık ve rastgele değişkenler, birleşik bir teori yardımıyla tek tip olarak ele alınabilir.

Olasılık Yoğunluk Fonksiyonunun formülü

Sabit bir x değeri üzerinde sürekli bir rastgele değişken X'in olasılığı her zaman 0'dır. Bu durumda, P(X = x) kullanılamaz. Bir değer aralığı (a,b) arasında yer alan X'in değeri belirlenmelidir. Aynısını belirlemek için aşağıdaki formül kullanılır.

Olasılık Yoğunluk Fonksiyonunun Özellikleri

Örneğin, (a,b) aralığı arasında değerini alan sürekli bir rastgele değişken, eğrinin altındaki alan ve (a) alt limiti ve (b) alt limiti olarak çizilen X ekseni hesaplanarak tahmin edilecektir. üst sınır. Yukarıdakiler için olasılık yoğunluk fonksiyonu şu şekilde temsil edilir:

Olasılık yoğunluğu işlevi, tüm olası değerler için pozitiftir (negatif değildir). Bu, her x için f(x)≥ 0 anlamına gelir. Yoğunluk eğrisi ile X ekseni (yatay eksen) arasına düşen alan 1'e eşittir.

Bu aynı zamanda şu şekilde de ifade edilebilir:

Yoğunluk fonksiyonu eğrisi, bir dizi sürekli değere veya değişkenin alanına karşı açıkça tanımlanan, verilen aralık boyunca süreklidir.

Kariyerinizi hızlandırmak için Makine Öğrenimi Kursuna, Makine Öğrenimi ve Yapay Zeka alanında Dünyanın en iyi Üniversiteleri - Yüksek Lisanslar, Yönetici Yüksek Lisans Programları ve İleri Düzey Sertifika Programından çevrimiçi katılın.

Olasılık Yoğunluk Fonksiyonunun Uygulamaları

• Olasılık yoğunluk fonksiyonu, atmosferik NO konsantrasyon seviyelerinin yıllık modellenmesinde kullanılır.
• Dizel motor yanmasının modellenmesi.
• İstatistikte, rastgele bir değişkenin sonucunun olasılıklarını belirlemek için olasılık yoğunluk fonksiyonu kullanılır.

Olasılık Yoğunluk Fonksiyonu Örnekleri

• örnek 1

Aşağıda, bir yatırımcının borsadaki risk potansiyelini belirlemek için olasılık yoğunluk fonksiyonunun (PDF) nasıl kullanıldığına dair bir örnek verilmiştir:

İlk olarak, PDF'ler tarihsel bilgilere dayalı bir grafik aracı olarak oluşturulur.

PDF'nin en yaygın biçimi, riskin çeşitli olasılıklarda ödüle eşit olduğu tarafsız projeksiyondur. Daha az risk alma kabiliyetine sahip yatırımcılar sadece sınırlı karlarla ödüllendirilecek ve bu nedenle çan eğrisinin sol tarafının altına giriyorlar. Tersine, yüksek risk alma kabiliyetine sahip yatırımcıların daha yüksek getiri ile ödüllendirilmeleri muhtemeldir ve bu nedenle eğrinin sağ tarafının altına düşerler.

Yatırımcıların çoğu ortalama risk alma yeteneğinin altındadır ve bu nedenle eğrinin ortasında yer alırlar.

Bu, alınan verilere dayalı olarak yatırımcı kategorisinin analiz edilmesine yardımcı olur. Bu, borsa komisyoncularının ürünlerini satmak için hedef müşteri kategorilerini belirlemelerine yardımcı olur.

• Örnek 2

Olasılık yoğunluk fonksiyonunun temel uygulamalarından biri, normal rastgele değişken olarak da bilinen Gauss rastgele değişkenidir.

Her iki durumda da grafik, olasılık yoğunluk fonksiyonu için bir çan eğrisi verir.

Yoğunluk şu şekilde ifade edilebilir:

Yukarıdaki yoğunluk denkleminin grafiği aşağıda verilmiştir.

Eğrinin altındaki alan, Gauss rastgele değişkeninin gerçek değerini temsil eder.

Çözüm

Olasılık yoğunluğu işlevi, makine öğreniminde hayati bir rol oynar. Makine Öğrenimi ve Yapay Zeka alanında kariyer hedefleyen öğrenciler için upGrad'ın Makine Öğreniminde IIT-İleri Düzey Sertifika Programına kaydolmalarını önemle tavsiye ederiz . Program, üst düzey çalışan profesyonelleri, bulut bilişim teknolojisini kullanarak makine öğrenimi modellerini dağıtmak üzere donatmak üzere özelleştirilmiş ve tasarlanmıştır.

Müfredat, öğrenme sürecini daha alakalı ve pratik hale getirmek için IIT Madras'tan öğretim üyeleri ve endüstri uzmanları tarafından tasarlanmıştır. Program, Hindistan'daki imrenilen ve 1 numaralı Mühendislik kolejinden dünya çapında tanınan sertifika ve upGrad'dan 360 derecelik yerleştirme desteği sunar.

Dahası, upGrad'ın 40.000'den fazla ücretli öğrenci tabanıyla büyük ölçekli projelerde işbirliği yapmak için sayısız fırsat elde edersiniz.

Öğrenme yolculuğunuza başlamak için web sitemize gidin!