Makine Öğreniminde Çok Değişkenli Regresyona Giriş: Eksiksiz Kılavuz

Günümüz teknolojisinin veri odaklı olduğu bir sır değil. Veriler yalnızca rakamların bir derlemesi olabilir, ancak işletmelerin uzun vadede rekabetçi ve sürdürülebilir kalması için üretkenliği ve becerikliliği çıkarmak için anlamlı bir şekilde işlenebilir. Olduğu gibi, veri analizi, ham bilgiden doğru tahminler elde etmenin cevabıdır.

Veri Analizi, verileri incelemek, işlemek ve kullanılabilir bir forma dönüştürmek için istatistiksel ve mantıksal fikirleri içeren bir tekniktir. Veri analizi ile çizilen çözümler, işletmelerde hayati kararlar almak için kullanılmaktadır. Veri bilimi ile birlikte veri analizi, gelecekteki sonuçları yüksek doğrulukla tahmin etmek için kullanılır. Bir veri havuzundan geçerli bilgiler elde etmek için bilimsel teknikleri ve algoritmaları kullanma sürecidir.

Veri uzmanlarının karşılaştığı yaygın bir sorun, bir yanıt değişkeni (Y ile gösterilir) ile açıklayıcı değişkenler (Xi ile gösterilir) arasında istatistiksel bir ilişkinin olup olmadığını belirleme yöntemidir.

Bu endişenin cevabı regresyon analizidir. Bunu daha ayrıntılı olarak anlayalım.

Regresyon Analizi Nedir?

Regresyon analizi, kontrollü veya denetimli bir makine öğrenme algoritmasını izleyen veri analizinde popüler yöntemlerden biridir. Verilerdeki değişkenler arasında ilişki belirlemek ve ilişki kurmak için etkili bir tekniktir.

Regresyon analizi, bu sıralanmış değişkenler hakkında son derece doğru sonuçlar çıkarmak için matematiksel stratejiler kullanarak uygulanabilir değişkenleri ayırmayı içerir.

Çok Değişkenli Regresyon Nedir?

Çok Değişkenli, birden çok veri değişkenini analiz eden kontrollü veya denetimli bir Makine Öğrenimi algoritmasıdır. Bir bağımlı değişken ve birçok bağımsız değişken içeren çoklu regresyonun devamıdır. Çıktı, bağımsız değişkenlerin sayısına göre tahmin edilir.

Çok değişkenli regresyon, değişkenlerde bulunan faktörlerin diğerlerindeki değişikliklere eşzamanlı tepkisini açıklayan bir formül bulur. Verileri çeşitli alanlarda incelemek için kullanılırlar. Örneğin, gayrimenkulde çok değişkenli regresyon, konumu, oda sayısı ve mevcut olanaklar gibi çeşitli faktörlere dayalı olarak bir evin fiyatını tahmin etmek için kullanılır.

Çok Değişkenli Regresyonda Maliyet Fonksiyonu

Maliyet işlevi, bir modelin sonucu gözlemlenen verilerden saptığında örneklere bir maliyet tahsis eder. Maliyet fonksiyonu denklemi, tahmin edilen değer ile gerçekleşen değer arasındaki farkın karesinin toplamının veri setinin uzunluğunun iki katına bölümüdür.

İşte bir örnek :

Sonuç :

Kaynak

Çok Değişkenli Regresyon Analizi nasıl kullanılır?

Çok değişkenli regresyon analizinde yer alan süreçler, öznitelik seçimi, öznitelik mühendisliği, öznitelik normalizasyonu, seçim kaybı fonksiyonları, hipotez analizi ve bir regresyon modeli oluşturmayı içerir.

1. Öznitelik seçimi: Çok değişkenli regresyonda en önemli adımdır. Değişken seçimi olarak da bilinen bu süreç, verimli modeller oluşturmak için uygun değişkenlerin seçilmesini içerir.
2. Özellik Normalleştirme: Bu, akıcı dağıtım ve veri oranlarını korumak için özellik ölçeklendirmeyi içerir. Bu, daha iyi veri analizine yardımcı olur. Tüm özelliklerin değeri ihtiyaca göre değiştirilebilir.
3. Kayıp fonksiyonu ve hipotez seçimi : Kayıp fonksiyonu, hataları tahmin etmek için kullanılır. Hipotez tahmini gerçek rakamlardan değiştiğinde kayıp fonksiyonu devreye girer. Burada hipotez, özellik veya değişkenden tahmin edilen değeri temsil eder.
4. Sabitleme hipotez parametresi : Hipotezin parametresi, kayıp fonksiyonunu en aza indirecek ve daha iyi tahmini geliştirecek şekilde sabitlenir veya ayarlanır.
5. Kayıp fonksiyonunun azaltılması : Kayıp fonksiyonu, veri setinde özellikle kayıp minimizasyonu için bir algoritma üretilerek minimize edilir ve bu da hipotez parametrelerinin değiştirilmesini kolaylaştırır. Gradyan iniş, kayıp minimizasyonu için en yaygın kullanılan algoritmadır. Algoritma, kayıp minimizasyonu tamamlandıktan sonra diğer eylemler için de kullanılabilir.
6. Hipotez fonksiyonunun analiz edilmesi : Değerlerin tahmin edilmesi için çok önemli olduğu için hipotezin fonksiyonunun analiz edilmesi gerekir. Fonksiyon analiz edildikten sonra test verileri üzerinde test edilir.

Şimdi çok değişkenli regresyonun kullanılabileceği iki yola bakalım.

1. Çok Değişkenli Doğrusal Regresyon

Çok değişkenli doğrusal regresyon, çok değişkenli doğrusal regresyonda birden çok bağımsız değişkenin bağımlı değişkenlere katkıda bulunması ve dolayısıyla hesaplamada birden çok katsayı kullanılması dışında basit doğrusal regresyona benzer.

• Birden çok rastgele değişken arasında matematiksel bir ilişki türetmek için kullanılır. Bir bağımlı değişkenle kaç tane bağımsız değişkenin ilişkili olduğunu açıklar.
• Sonuç değişkeni üzerindeki etkilerinin doğru bir tahminini yapmak için birden fazla bağımsız değişkenin ayrıntıları kullanılır.
• Çok değişkenli doğrusal regresyon modeli, her veri noktasının en iyi yaklaşımıyla doğrusal bir biçimde (düz bir çizgi biçiminde) bir ilişki oluşturur.
• Çok değişkenli doğrusal regresyon modelinin denklemi:

yi​=β0​+β1​xi1​+β2​xi2​+…+βp​xip​+

i=n gözlemler için:

Kaynak

Doğrusal regresyon ne zaman kullanılabilir?

Doğrusal regresyon modeli, yalnızca biri bağımlı, diğeri bağımsız olan iki sürekli değişken olduğunda kullanılabilir.

Bağımsız değişken, bağımlı değişkenin değerini veya sonucunu belirlemek için bir parametre olarak kullanılır.

2. Çok Değişkenli Lojistik Regresyon

Lojistik regresyon, birden çok bağımsız değişkene dayalı ikili bir sonucu tahmin etmek için kullanılan bir algoritmadır. İkili bir sonucun iki olasılığı vardır, senaryo gerçekleşir (1 ile gösterilir) veya gerçekleşmez (0 ile gösterilir).

Lojistik regresyon, sonucun (veya bağımlı değişkenin) ikili olduğu veriler olan ikili veriler üzerinde çalışırken kullanılır.

Lojistik regresyon nerelerde kullanılabilir?

Lojistik regresyon öncelikle sınıflandırma sorunlarıyla başa çıkmak için kullanılır. Örneğin, bir e-postanın spam olup olmadığını ve belirli bir işlemin kötü amaçlı olup olmadığını belirlemek için. Veri analizinde, kayıpları en aza indirgemek ve karı artırmak için hesaplanmış kararlar vermek için kullanılır.

Çok değişkenli lojistik regresyon, bir bağımlı değişken ve birden çok sonuç olduğunda kullanılır. İkiden fazla olası sonuca sahip olmasıyla lojistik regresyondan farklıdır.

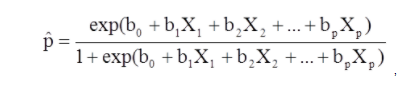
X1 ila Xp farklı bağımsız değişkenlerdir.

b0 ila bp regresyon katsayılarıdır

Çoklu lojistik regresyon modeli farklı bir biçimde de yazılabilir. Aşağıdaki formda, sonuç, sonucun mevcut olma ihtimalinin beklenen günlüğüdür,

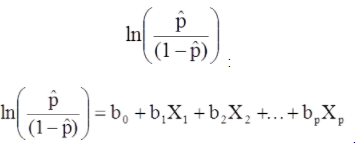
Çoklu lojistik regresyon modeli farklı bir biçimde de yazılabilir. Aşağıdaki formda, sonuç, sonucun mevcut olması ihtimalinin beklenen günlüğüdür.

Yukarıdaki denklemin sağ tarafı lineer regresyon denklemine benzer ancak regresyon katsayılarını bulma yöntemi farklıdır.

Çok Değişkenli Regresyon Modelindeki Varsayımlar

• Bağımlı ve bağımsız değişkenler arasında doğrusal bir ilişki vardır.
• Bağımsız değişkenler kendi aralarında güçlü bir ilişkiye sahip değildir.
• yi gözlemleri popülasyondan rastgele ve bireysel olarak seçilir.

Çok Değişkenli Lojistik Regresyon Modelinde Varsayımlar

• Bağımlı değişken nominal veya sıralıdır. Nominal değişkenler, anlamlı bir organizasyonu olmayan iki veya daha fazla kategoriye sahiptir. Sıralı değişkenler ayrıca iki veya daha fazla kategoriye sahip olabilir, ancak bir yapıları vardır ve sıralanabilirler.
• Sıralı, sürekli veya nominal olabilen tek veya çoklu bağımsız değişkenler olabilir. Sürekli değişkenler, belirli bir aralıkta sonsuz değerlere sahip olabilen değişkenlerdir.
• Bağımlı değişkenler birbirini dışlayan ve kapsamlıdır.
• Bağımsız değişkenler kendi aralarında güçlü bir ilişkiye sahip değildir.

Çok Değişkenli Regresyonun Avantajları

1. Çok değişkenli regresyon, veri kümesindeki birden çok değişken arasındaki ilişkileri incelememize yardımcı olur.
2. Bağımlı ve bağımsız değişkenler arasındaki korelasyon, sonucun tahmin edilmesine yardımcı olur.
3. Makine öğreniminde kullanılan en kullanışlı ve popüler algoritmalardan biridir.

Çok Değişkenli Regresyonun Dezavantajları

• Çok değişkenli tekniklerin karmaşıklığı, karmaşık matematiksel hesaplamalar gerektirir.
• Kayıp ve hata çıktılarında tutarsızlıklar olduğu için çok değişkenli regresyon modelinin çıktısını yorumlamak kolay değildir.
• Çok değişkenli regresyon modelleri daha küçük veri kümelerine uygulanamaz; daha büyük veri kümeleri söz konusu olduğunda doğru çıktılar üretmek için tasarlanmıştır.

Çok değişkenli regresyon ve diğer karmaşık veri bilimi konuları hakkında daha fazla bilgi edinmek istiyorsanız, upGrad'da tam size göre bir çözüm var. Liverpool John Moores Üniversitesi'nden Veri Bilimi alanında 18 aylık Master of Science kursumuz 500'den fazla zorlu öğrenme saatini, 25 koçluk seansını (1:8 temelinde gerçekleştirilir) ve 20'den fazla canlı seansı kapsar. upGrad ayrıca öğrencilerin kariyerlerini dönüştürmeleri için 1:1 öğretim yardımı ve 360° kariyer rehberliği desteği sunar. Öğrenciler, 40.000'den fazla ücretli öğrenciyle küresel platformda eşler arası öğrenimden yararlanabilir ve öğrenim deneyimlerini en üst düzeye çıkarmak için altı işlevsel uzmanlıkta ortak projeler üzerinde çalışabilir.