Makine Öğreniminde Gradyan İnişi: Nasıl Çalışır?

Tanıtım

Makine Öğreniminin en önemli kısımlarından biri, algoritmalarının optimizasyonudur. Makine Öğrenimi'ndeki hemen hemen tüm algoritmaların temelinde, algoritmanın çekirdeğini oluşturan bir optimizasyon algoritması bulunur. Hepimizin bildiği gibi, optimizasyon, gerçek hayattaki olaylarla veya piyasadaki teknoloji tabanlı bir ürünle uğraşırken bile herhangi bir algoritmanın nihai hedefidir.

Halihazırda yüz tanıma, kendi kendini süren arabalar, pazar tabanlı analiz vb. gibi çeşitli uygulamalarda kullanılan birçok optimizasyon algoritması bulunmaktadır. Benzer şekilde, Makine Öğreniminde bu tür optimizasyon algoritmaları önemli bir rol oynamaktadır. Böyle yaygın olarak kullanılan bir optimizasyon algoritması, bu makalede inceleyeceğimiz Gradient Descent Algoritmasıdır.

Gradyan İniş Nedir?

Makine Öğreniminde Gradient Descent algoritması en çok kullanılan algoritmalardan biridir ve yine de yeni gelenlerin çoğunu şaşkına çevirir. Matematiksel olarak Gradient Descent, türevlenebilir bir fonksiyonun yerel minimumunu bulmak için kullanılan birinci dereceden yinelemeli bir optimizasyon algoritmasıdır. Basit bir ifadeyle, bu Gradient Descent algoritması, bir maliyet fonksiyonunu mümkün olduğunca düşük en aza indirmek için kullanılan bir fonksiyonun parametrelerinin (veya katsayılarının) değerlerini bulmak için kullanılır. Maliyet işlevi, oluşturulmuş bir Makine Öğrenimi modelinin tahmin edilen değerleri ile gerçek değerleri arasındaki hatayı ölçmek için kullanılır.

Gradyan İniş Sezgisi

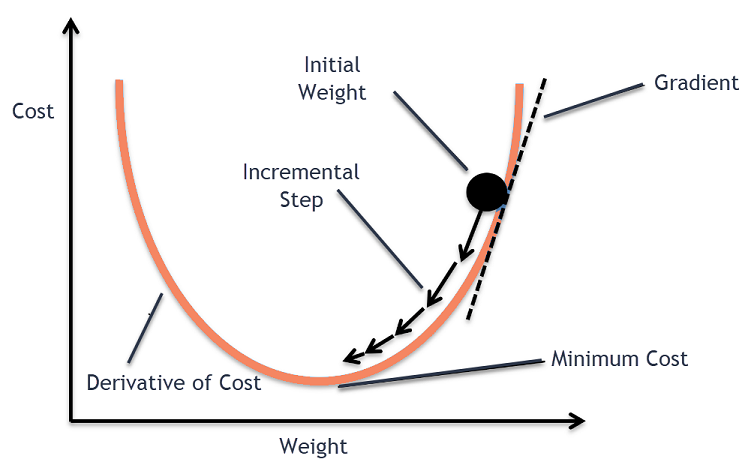
Normalde meyveleri saklayacağınız veya mısır gevreği yiyebileceğiniz büyük bir kase düşünün. Bu kase maliyet fonksiyonu (f) olacaktır.

Şimdi, kasenin yüzeyinin herhangi bir yerindeki rastgele bir koordinat, maliyet fonksiyonunun katsayılarının mevcut değerleri olacaktır. Kasenin dibi en iyi katsayılar kümesidir ve fonksiyonun minimumudur.

Burada amaç, her bir iterasyonda katsayıların farklı değerlerini hesaplamak, maliyeti değerlendirmek ve daha iyi bir maliyet fonksiyonu değerine (daha düşük değer) sahip olan katsayıları seçmektir. Birden fazla yinelemede, kasenin tabanının maliyet fonksiyonunu en aza indirmek için en iyi katsayılara sahip olduğu bulunacaktı.

Bu şekilde, Gradient Descent algoritması minimum maliyetle sonuçlanacak şekilde çalışır.

Kariyerinizi hızlandırmak için Makine Öğrenimi Kursuna , Makine Öğrenimi ve Yapay Zeka alanında Dünyanın en iyi Üniversiteleri - Yüksek Lisanslar, Yönetici Yüksek Lisans Programları ve İleri Düzey Sertifika Programından çevrimiçi katılın .

Gradyan İniş Prosedürü

Bu gradyan iniş süreci, değerlerin başlangıçta maliyet fonksiyonunun katsayılarına tahsis edilmesiyle başlar. Bu, 0'a yakın bir değer veya küçük bir rastgele değer olabilir.

katsayı = 0.0

Daha sonra katsayıların maliyeti, maliyet fonksiyonuna uygulanarak ve maliyet hesaplanarak elde edilir.

maliyet = f(katsayı)

Daha sonra maliyet fonksiyonunun türevi hesaplanır. Maliyet fonksiyonunun bu türevi, diferansiyel hesabın matematiksel kavramıyla elde edilir. Bize fonksiyonun türevinin hesaplandığı noktadaki eğimini verir. Bu eğim, daha düşük bir maliyet değeri elde etmek için bir sonraki iterasyonda katsayının hangi yönde hareket ettirileceğini bilmek için gereklidir. Bu, hesaplanan türevin işareti gözlemlenerek yapılır.

delta = türev(maliyet)

Hesaplanan türevden hangi yönün yokuş aşağı olduğunu öğrendiğimizde, katsayı değerlerini güncellememiz gerekir. Bunun için öğrenme parametresi olarak bilinen bir parametre alfa (α) kullanılır. Bu, katsayıların her güncellemede ne ölçüde değişebileceğini kontrol etmek için kullanılır.

katsayı = katsayı – (alfa * delta)

Kaynak

Bu şekilde, katsayıların maliyeti 0,0'a eşit veya sıfıra yeterince yakın olana kadar bu işlem tekrarlanır. Gradyan iniş algoritması için prosedür budur.

Gradyan İniş Algoritmaları Türleri

Modern zamanlarda, modern makine öğrenimi ve derin öğrenme algoritmalarında kullanılan üç temel Gradient Descent türü vardır. Bu 3 türün her biri arasındaki en büyük fark, hesaplama maliyeti ve verimliliğidir. Kullanılan veri miktarına, zamanın karmaşıklığına ve doğruluğuna bağlı olarak aşağıdakiler üç tiptir.

1. Toplu Gradyan İniş
2. Stokastik Gradyan İniş
3. Mini Toplu Degrade İniş

Toplu Gradyan İniş

Bu, maliyet fonksiyonunu ve gradyanını hesaplamak için tüm veri setinin bir kerede kullanıldığı Gradient Descent algoritmalarının ilk ve temel versiyonudur. Tüm veri seti tek bir güncelleme için tek seferde kullanıldığından, bu tipteki gradyan hesaplaması çok yavaş olabilir ve cihazın hafıza kapasitesini aşan veri setleri ile mümkün değildir.

Bu nedenle, bu Toplu Gradyan İniş algoritması yalnızca daha küçük veri kümeleri için kullanılır ve eğitim örneklerinin sayısı fazla olduğunda toplu gradyan inişi tercih edilmez. Bunun yerine Stokastik ve Mini Toplu Gradyan İniş algoritmaları kullanılır.

Stokastik Gradyan İniş

Bu, yineleme başına yalnızca bir eğitim örneğinin işlendiği başka bir gradyan iniş algoritması türüdür. Bunda ilk adım, tüm eğitim veri setini rastgele seçmektir. Daha sonra katsayıları güncellemek için sadece bir eğitim örneği kullanılır. Bu, parametrelerin (katsayıların) yalnızca tüm eğitim örnekleri değerlendirildiğinde güncellendiği Toplu Gradyan İnişinin aksinedir.

Stokastik Gradyan Düşüşü (SGD), bu tür sık ​​güncellemenin ayrıntılı bir iyileştirme oranı sağlaması avantajına sahiptir. Bununla birlikte, bazı durumlarda, yineleme sayısının çok büyük olmasına neden olabilecek her yinelemede yalnızca bir örnek işlediğinden bu, hesaplama açısından pahalı olabilir.

Mini Toplu Degrade İniş

Bu, hem Batch hem de Stokastik Gradyan İniş algoritmalarından daha hızlı olan, yakın zamanda geliştirilmiş bir algoritmadır. Daha önce bahsedilen her iki algoritmanın bir kombinasyonu olduğu için çoğunlukla tercih edilir. Bunda, eğitim setini birkaç mini partiye ayırır ve bu partinin gradyanını hesapladıktan sonra (SGD'de olduğu gibi) bu partilerin her biri için bir güncelleme gerçekleştirir.

Genellikle parti boyutu 30 ile 500 arasında değişir, ancak farklı uygulamalar için değişiklik gösterdiğinden sabit bir boyut yoktur. Bu nedenle, çok büyük bir eğitim veri seti olsa bile, bu algoritma onu 'b' mini-partilerinde işler. Bu nedenle, daha az sayıda yinelemeli büyük veri kümeleri için uygundur.

Eğer 'm' eğitim örneklerinin sayısıysa, o zaman b==m ise Mini Toplu Dereceli İniş, Toplu Dereceli İniş algoritmasına benzer olacaktır.

Makine Öğreniminde Gradient Descent Varyantları

Gradient Descent için bu temel ile, bundan geliştirilmiş birkaç başka algoritma vardır. Bunlardan birkaçı aşağıda özetlenmiştir.

Vanilya Gradyan İniş

Bu, Gradyan İniş Tekniğinin en basit biçimlerinden biridir. Vanilya adı, saf veya herhangi bir katkısız anlamına gelir. Bunda, maliyet fonksiyonunun gradyanı hesaplanarak minimumlar yönünde küçük adımlar atılır. Yukarıda belirtilen algoritmaya benzer şekilde, güncelleme kuralı şu şekilde verilir:

katsayı = katsayı – (alfa * delta)

Momentumlu Gradyan İniş

Bu durumda, algoritma, bir sonraki adımı atmadan önce önceki adımları bildiğimiz şekildedir. Bu, önceki güncellemenin ürünü olan yeni bir terim ve momentum olarak bilinen bir sabit tanıtılarak yapılır. Bunda ağırlık güncelleme kuralı şu şekilde verilir:

güncelleme = alfa * delta

hız = önceki_güncelleme * momentum

katsayı = katsayı + hız - güncelleme

ADAGRAD

ADAGRAD terimi, Uyarlanabilir Gradyan Algoritması anlamına gelir. Adından da anlaşılacağı gibi, ağırlıkları güncellemek için uyarlanabilir bir teknik kullanır. Bu algoritma seyrek veriler için daha uygundur. Bu optimizasyon, eğitim sırasında parametre güncellemelerinin sıklığına göre öğrenme oranlarını değiştirir. Örneğin, daha yüksek gradyanlara sahip olan parametreler, minimum değeri aşmamak için daha yavaş bir öğrenme oranına sahip olacak şekilde yapılır. Benzer şekilde, daha düşük eğimler, daha hızlı eğitim almak için daha hızlı bir öğrenme oranına sahiptir.

ADAM

Kökleri Gradient Descent algoritmasında olan bir başka uyarlamalı optimizasyon algoritması, Adaptive Moment Estimation anlamına gelen ADAM'dir. Hem ADAGRAD hem de SGD'nin Momentum algoritmalarıyla birleşimidir. ADAGRAD algoritmasından oluşturulmuştur ve daha da olumsuz olarak oluşturulmuştur. Basit bir ifadeyle ADAM = ADAGRAD + Momentum.

Bu şekilde AMSGrad, ADMax gibi dünyada geliştirilmiş ve geliştirilmekte olan birkaç Gradient Descent Algoritma varyantı vardır.

Çözüm

Bu yazımızda, Makine Öğreniminde en sık kullanılan optimizasyon algoritmalarından biri olan Gradient Descent Algorithms'in arkasındaki algoritmayı, geliştirilmiş türleri ve varyantları ile birlikte gördük.

upGrad, Makine Öğrenimi ve Yapay Zeka alanında bir Yönetici PG Programı ve Makine Öğrenimi ve Yapay Zeka alanında size bir kariyer inşa etme yolunda rehberlik edebilecek bir Yüksek Lisans Programı sunar. Bu kurslar, Makine Öğrenimi ihtiyacını ve Makine Öğreniminde Gradient Descent'e kadar uzanan çeşitli kavramları kapsayan bu alanda bilgi toplamak için sonraki adımları açıklayacaktır.