Gauss Naive Bayes: Bilmeniz Gerekenler?
Yayınlanan: 2021-02-22İçindekiler
Gauss Saf Bayes
Naive Bayes, birçok sınıflandırma işlevi için kullanılan olasılıksal bir makine öğrenme algoritmasıdır ve Bayes teoremine dayalıdır. Gauss Naive Bayes, saf Bayes'in uzantısıdır. Veri dağılımını tahmin etmek için diğer işlevler kullanılırken, eğitim verileri için ortalama ve standart sapmayı hesaplamanız gerekeceğinden, Gauss veya normal dağılım uygulanması en basit olanıdır.
Naive Bayes Algoritması nedir?
Naive Bayes, çeşitli sınıflandırma görevlerinde kullanılabilen olasılıklı bir makine öğrenme algoritmasıdır. Naive Bayes'in tipik uygulamaları, belgelerin sınıflandırılması, istenmeyen postaların filtrelenmesi, tahmin vb. Bu algoritma, Thomas Bayes'in keşiflerine ve dolayısıyla ismine dayanmaktadır.
Algoritmanın modelinde birbirinden bağımsız özellikler içermesi nedeniyle “Naif” adı kullanılmıştır. Bir özelliğin değerindeki herhangi bir değişiklik, algoritmanın diğer herhangi bir özelliğinin değerini doğrudan etkilemez. Naive Bayes algoritmasının temel avantajı, basit ama güçlü bir algoritma olmasıdır.
Algoritmanın kolayca kodlanabildiği ve tahminlerin gerçek zamanlı olarak hızlı bir şekilde yapıldığı olasılık modeline dayanmaktadır. Dolayısıyla bu algoritma, kullanıcı isteklerine anında yanıt verecek şekilde ayarlanabildiğinden, gerçek dünya sorunlarını çözmek için tipik bir seçimdir. Ancak, Naive Bayes ve Gaussian Naive Bayes'in derinliklerine dalmadan önce, koşullu olasılığın ne anlama geldiğini bilmeliyiz.
Koşullu Olasılık Açıklaması
Koşullu olasılığı bir örnekle daha iyi anlayabiliriz. Yazı tura attığınızda öne geçme veya yazı gelme olasılığı %50'dir. Benzer şekilde, yüzleri olan zarları attığınızda 4 gelme olasılığı 1/6 veya 0.16'dır.
Bir deste kart alırsak, maça olması koşuluyla bir vezir elde etme olasılığı nedir? Maça olması koşulu önceden ayarlandığından, payda veya seçim seti 13 olur. Maçalarda sadece bir vezir vardır, dolayısıyla bir maça veziri seçme olasılığı 1/13= 0.07 olur.

A olayının belirli bir B olayının koşullu olasılığı, B olayının zaten meydana geldiği göz önüne alındığında A olayının meydana gelme olasılığı anlamına gelir. Matematiksel olarak, verilen B'nin koşullu olasılığı P[A|B] = P[A VE B] / P[B] olarak gösterilebilir.
Biraz karmaşık bir örnek düşünelim. Toplam 100 öğrencisi olan bir okul alın. Bu popülasyon 4 kategoriye ayrılabilir: Öğrenciler, Öğretmenler, Erkekler ve Kadınlar. Aşağıda verilen tabloyu göz önünde bulundurun:
| Dişi | Erkek | Toplam | |
| Öğretmen | 8 | 12 | 20 |
| Öğrenci | 32 | 48 | 80 |
| Toplam | 40 | 50 | 100 |
Burada, belirli bir okul sakininin Erkek olması koşuluyla Öğretmen olma koşullu olasılığı nedir?
Bunu hesaplamak için 60 erkekten oluşan alt popülasyonu filtrelemeniz ve 12 erkek öğretmene kadar inmeniz gerekecek.
Yani, beklenen koşullu olasılık P[Öğretmen | Erkek] = 12/60 = 0,2
P (Öğretmen | Erkek) = P (Öğretmen ∩ Erkek) / P(Erkek) = 12/60 = 0,2
Bu, bir Öğretmen(A) ve Erkek(B), Erkek(B)'ye bölünerek temsil edilebilir. Benzer şekilde, A verilen B'nin koşullu olasılığı da hesaplanabilir. Naive Bayes için kullandığımız kural aşağıdaki gösterimlerden çıkarılabilir:
P (A | B) = P (A ∩ B) / P(B)
P (B | A) = P (A ∩ B) / P(A)
Bayes Kuralı
Bayes kuralında, eğitim veri setinden bulunabilen P (X | Y) den P (Y | X) bulmak için gidiyoruz. Bunu başarmak için tek yapmanız gereken yukarıdaki formüllerde A ve B'yi X ve Y ile değiştirmek. Gözlemler için X bilinen değişken, Y ise bilinmeyen değişken olacaktır. Veri kümesinin her satırı için, X'in zaten gerçekleştiğine göre Y olasılığını hesaplamanız gerekir.
Ancak Y'de 2'den fazla kategori olduğunda ne olur? Kazananı bulmak için her Y sınıfının olasılığını hesaplamalıyız.
Bayes kuralıyla, P (X | Y)'den P (Y | X)'i bulmak için gidiyoruz.
Eğitim verilerinden bilinir: P (X | Y) = P (X ∩ Y) / P(Y)
P (Kanıt | Sonuç)
Bilinmiyor – test verileri için tahmin edilecek: P (Y | X) = P (X ∩ Y) / P(X)

P (Sonuç | Kanıt)
Bayes Kuralı = P (Y | X) = P (X | Y) * P (Y) / P (X)
Naif Bayes
Bayes kuralı, verilen X koşulunun Y olasılığının formülünü sağlar. Ancak gerçek dünyada, birden fazla X değişkeni olabilir. Bağımsız özelliklere sahip olduğunuzda, Bayes kuralı, Naive Bayes kuralına genişletilebilir. X'ler birbirinden bağımsızdır. Naive Bayes formülü, Bayes formülünden daha güçlüdür.
Gauss Saf Bayes
Buraya kadar X'lerin kategorilerde olduğunu gördük ama X sürekli bir değişken olduğunda olasılıkları nasıl hesaplayabiliriz? X'in belirli bir dağılımı izlediğini varsayarsak, olasılıkların olasılığını hesaplamak için bu dağılımın olasılık yoğunluğu işlevini kullanabilirsiniz.
X'lerin bir Gauss veya normal dağılım izlediğini varsayarsak, normal dağılımın olasılık yoğunluğunu değiştirmeli ve onu Gauss Naive Bayes olarak adlandırmalıyız. Bu formülü hesaplamak için X'in ortalamasına ve varyansına ihtiyacınız var.
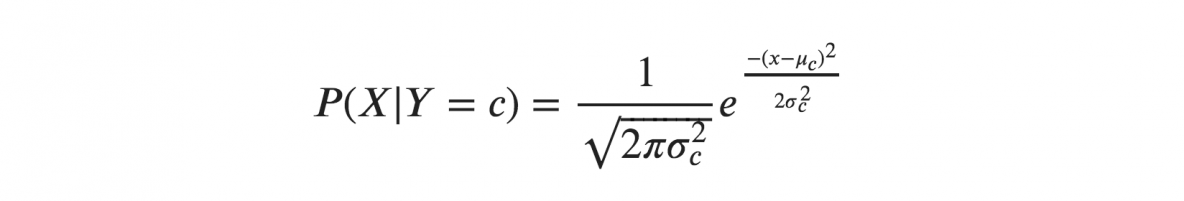
Yukarıdaki formüllerde, sigma ve mu, belirli bir Y sınıfı için hesaplanan sürekli değişken X'in varyansı ve ortalamasıdır.
Gauss Naive Bayes için Temsil
Yukarıdaki formül, bir frekans aracılığıyla her sınıf için giriş değerlerinin olasılıklarını hesapladı. Tüm dağılım için her sınıf için x'lerin ortalamasını ve standart sapmasını hesaplayabiliriz.
Bu, her sınıf için olasılıklarla birlikte, sınıf için her girdi değişkeni için ortalamayı ve standart sapmayı da saklamamız gerektiği anlamına gelir.
ortalama(x) = 1/n * toplam(x)
burada n, örnek sayısını temsil eder ve x, verilerdeki giriş değişkeninin değeridir.
standart sapma(x) = sqrt(1/n * toplam(xi-ortalama(x)^2 ))
Burada, her bir x'in ortalama farklarının karekökü ve x'in ortalaması hesaplanır; burada n, örnek sayısıdır, toplam(), toplam işlevidir, sqrt(), karekök işlevidir ve xi, belirli bir x değeridir. .

Gauss Naive Bayes Modeli ile Tahminler
Gauss olasılık yoğunluk işlevi, parametreleri değişkenin yeni giriş değeriyle değiştirerek tahminlerde bulunmak için kullanılabilir ve sonuç olarak Gauss işlevi, yeni giriş değerinin olasılığı için bir tahmin verecektir.
Saf Bayes Sınıflandırıcısı
Naive Bayes sınıflandırıcısı, bir özelliğin değerinin diğer herhangi bir özelliğin değerinden bağımsız olduğunu varsayar. Naive Bayes sınıflandırıcıları, sınıflandırma için gerekli parametreleri tahmin etmek için eğitim verilerine ihtiyaç duyar. Basit tasarımı ve uygulaması sayesinde Naive Bayes sınıflandırıcıları birçok gerçek hayat senaryosuna uygun olabilir.
Çözüm
Gaussian Naive Bayes sınıflandırıcı, çok fazla çaba harcamadan ve iyi bir doğruluk seviyesi olmadan çok iyi çalışan hızlı ve basit bir sınıflandırıcı tekniğidir.
Yapay zeka, makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, çalışan profesyoneller için tasarlanmış ve 450+ saatlik zorlu eğitim, 30'dan fazla vaka çalışması ve ödev sunan IIIT-B & upGrad'ın Makine Öğrenimi ve Yapay Zeka alanında PG Diplomasına göz atın. IIIT-B Mezun statüsü, 5+ pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.
Dünyanın En İyi Üniversitelerinden ML Kursu öğrenin . Kariyerinizi hızlandırmak için Master, Executive PGP veya Advanced Certificate Programları kazanın.
Saf bayes algoritması nedir?
Naive bayes, klasik bir makine öğrenimi algoritmasıdır. Kökeni istatistik olan saf bayes basit ve güçlü bir algoritmadır. Naive bayes, koşullu olasılık analizinin uygulanmasına dayanan bir sınıflandırıcı ailesidir. Bu analizde, bir olayın koşullu olasılığı, olayı oluşturan bireysel olayların her birinin olasılığı kullanılarak hesaplanır. Naive bayes sınıflandırıcılarının, özellikle özellik setinin boyutlarının sayısı büyük olduğunda, pratikte genellikle son derece etkili olduğu bulunmuştur.
Naive bayes algoritmasının uygulamaları nelerdir?
Naive Bayes, metin sınıflandırma, belge sınıflandırma ve belge indeksleme için kullanılır. Saf bölmelerde, olası her özelliğin ön işleme aşamasında atanan herhangi bir ağırlığı yoktur ve ağırlıklar daha sonra eğitim ve tanıma aşamaları sırasında atanır. Naive bayes algoritmasının temel varsayımı, özniteliklerin bağımsız olduğudur.
Gauss Naive Bayes algoritması nedir?
Gaussian Naive Bayes, Bayes teoreminin güçlü bağımsızlık varsayımları ile uygulanmasına dayanan olasılıksal bir sınıflandırma algoritmasıdır. Sınıflandırma bağlamında bağımsızlık, bir özelliğin bir değerinin varlığının diğerinin varlığını etkilemediği fikrine atıfta bulunur (olasılık teorisindeki bağımsızlığın aksine). Naive, bir nesnenin özelliklerinin birbirinden bağımsız olduğu varsayımının kullanılmasına atıfta bulunur. Makine öğrenimi bağlamında, saf Bayes sınıflandırıcılarının son derece anlamlı, ölçeklenebilir ve makul derecede doğru olduğu bilinmektedir, ancak eğitim setinin büyümesiyle performansları hızla bozulur. Saf Bayes sınıflandırıcılarının başarısına bir dizi özellik katkıda bulunur. En önemlisi, sınıflandırma modelinin parametrelerinin ayarlanmasını gerektirmezler, eğitim veri setinin boyutuyla iyi ölçeklenirler ve sürekli özellikleri kolayca işleyebilirler.
