Bilmeniz Gereken Farklı Regresyon Modelleri

Regresyon sorunları makine öğreniminde yaygındır ve bunları çözmek için en yaygın teknik regresyon analizidir. Veri modellemeye dayalıdır ve tüm veri noktalarından geçen, böylece hat ile her bir veri noktası arasındaki mesafe minimum olacak şekilde en uygun hattı bulmayı içerir. Birçok farklı regresyon analizi tekniği mevcut olmakla birlikte, lineer ve lojistik regresyon en belirgin olanlarıdır. Kullandığımız regresyon analizi modelinin türü, ilgili verilerin doğasına bağlı olacaktır.

Regresyon analizi ve farklı regresyon analizi modelleri hakkında daha fazla bilgi edelim.

Regresyon Analizi Nedir?

Regresyon analizi, bir veri setindeki bağımlı (hedef) değişkenler ile bağımsız değişkenler arasındaki ilişkiyi belirlemek için tahmine dayalı bir modelleme tekniğidir. Tipik olarak, hedef değişken sürekli değerler içerdiğinde ve bağımlı ve bağımsız değişkenler doğrusal veya doğrusal olmayan bir ilişki paylaştığında kullanılır. Bu nedenle, regresyon analizi teknikleri, değişkenler, zaman serisi modellemesi ve tahmin arasındaki nedensel etki ilişkisini belirlemede kullanım bulur. Örneğin, bir şirketin satışları ve reklam harcamaları arasındaki ilişki, en iyi regresyon analizi kullanılarak incelenebilir.

Regresyon Analizi Türleri

Tahmin yapmak için kullanabileceğimiz birçok farklı türde regresyon analizi tekniği vardır. Ayrıca, her tekniğin kullanımı, bağımsız değişkenlerin sayısı, regresyon çizgisinin şekli ve bağımlı değişkenin türü gibi faktörler tarafından yönlendirilir.

En sık kullanılan regresyon analizi yöntemlerinden bazılarını anlayalım:

1. Doğrusal Regresyon

Doğrusal regresyon, en yaygın olarak bilinen modelleme tekniğidir ve bağımlı değişken (Y) ile bağımsız değişken (X) arasında doğrusal bir ilişki olduğunu varsayar. Bu doğrusal ilişkiyi, en uygun çizgi olarak da bilinen bir regresyon çizgisi kullanarak kurar. Doğrusal ilişki Y = c+m*X + e denklemi ile temsil edilir, burada 'c' kesişme noktası, 'm' doğrunun eğimi ve 'e' hata terimidir.

Doğrusal regresyon modeli basit (bir bağımlı ve bir bağımsız değişkenli) veya çoklu (bir bağımlı değişkenli ve birden fazla bağımsız değişkenli) olabilir.

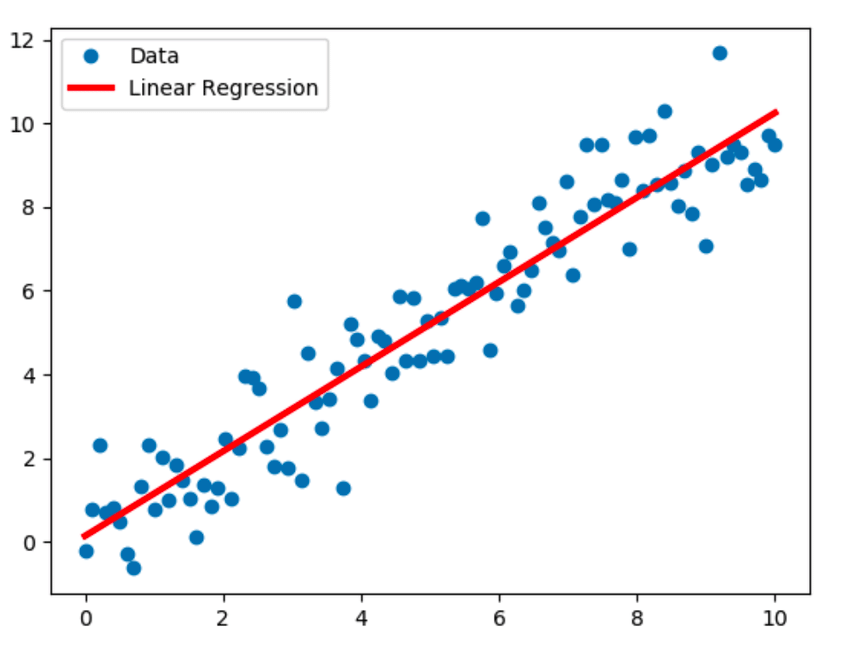
Kaynak

2. Lojistik Regresyon

Lojistik regresyon analizi tekniği, bağımlı değişken ayrık olduğunda kullanım bulur. Başka bir deyişle, bu teknik başarılı/başarısız, doğru/yanlış, 0/1 vb. gibi birbirini dışlayan olayların olasılığını tahmin etmek için kullanılır. Dolayısıyla, hedef değişken iki değerden yalnızca birine sahip olabilir ve bir sigmoid eğri aşağıdakileri temsil eder: bağımsız değişkenle ilişkisi. Olasılık değeri 0 ile 1 arasında değişir.

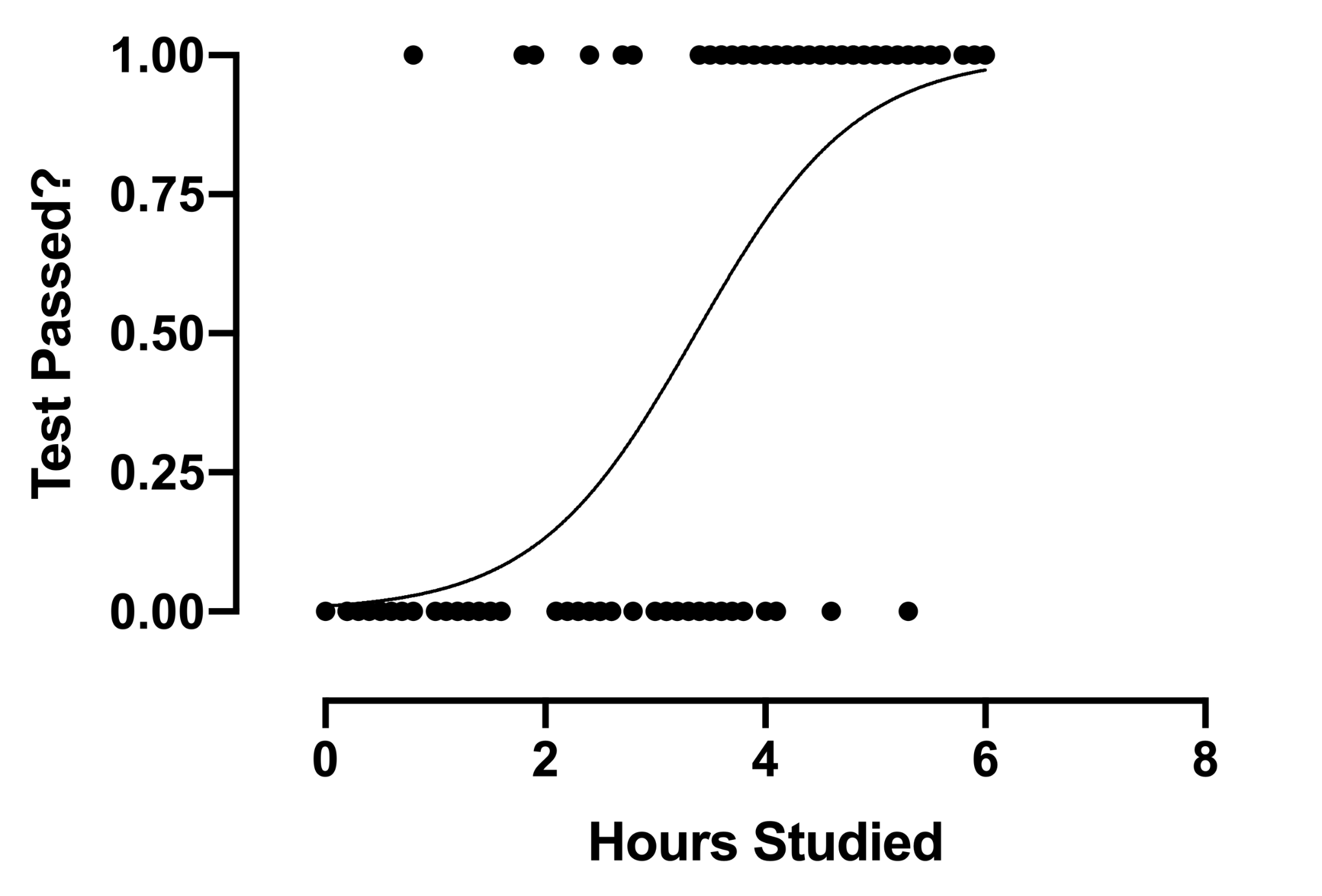
Kaynak

3. Polinom Regresyon

Polinom regresyon analizi tekniği, bağımlı ve bağımsız değişkenler arasında doğrusal olmayan bir ilişkiyi modeller. Çoklu doğrusal regresyon modelinin değiştirilmiş bir şeklidir, ancak tüm veri noktalarından geçen en uygun çizgi düz değil eğridir.

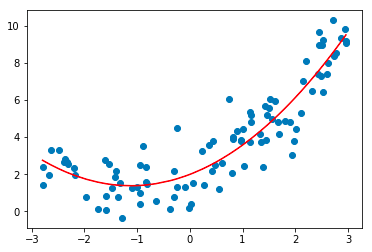
Kaynak

4. Sırt Regresyonu

Ridge regresyon analizi tekniği, veriler çoklu bağlantı gösterdiğinde kullanılır; yani, bağımsız değişkenler yüksek oranda ilişkilidir. Çoklu doğrusal bağlantıdaki en küçük kareler tahminleri yansız olmasına rağmen, varyansları gözlenen değeri gerçek değerden saptıracak kadar büyüktür. Ridge regresyonu, regresyon tahminlerine bir derece sapma getirerek standart hataları en aza indirir.

Sırt regresyon denklemindeki lambda (λ), çoklu bağlantı problemini çözer.

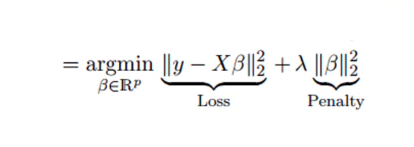
Kaynak

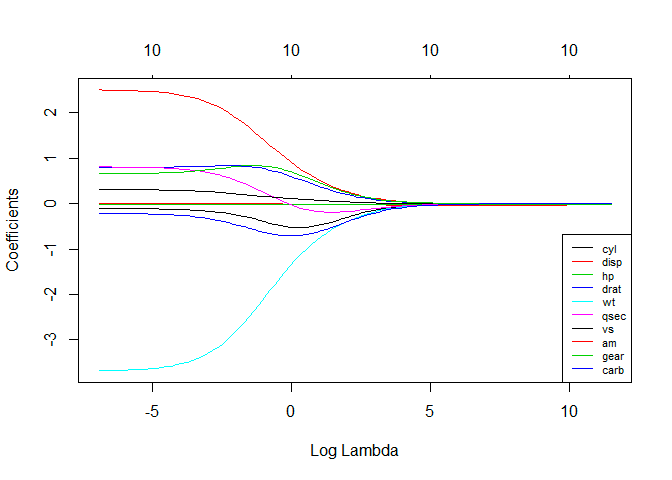
Kaynak

5. Kement Regresyonu

Sırt regresyonu gibi, kement (En Az Mutlak Büzülme ve Seçim Operatörü) regresyon tekniği de regresyon katsayısının mutlak boyutunu cezalandırır. Ek olarak, kement regresyon tekniği değişken seçimini kullanır, bu da katsayı değerlerinin mutlak sıfıra doğru daralmasıyla sonuçlanır.

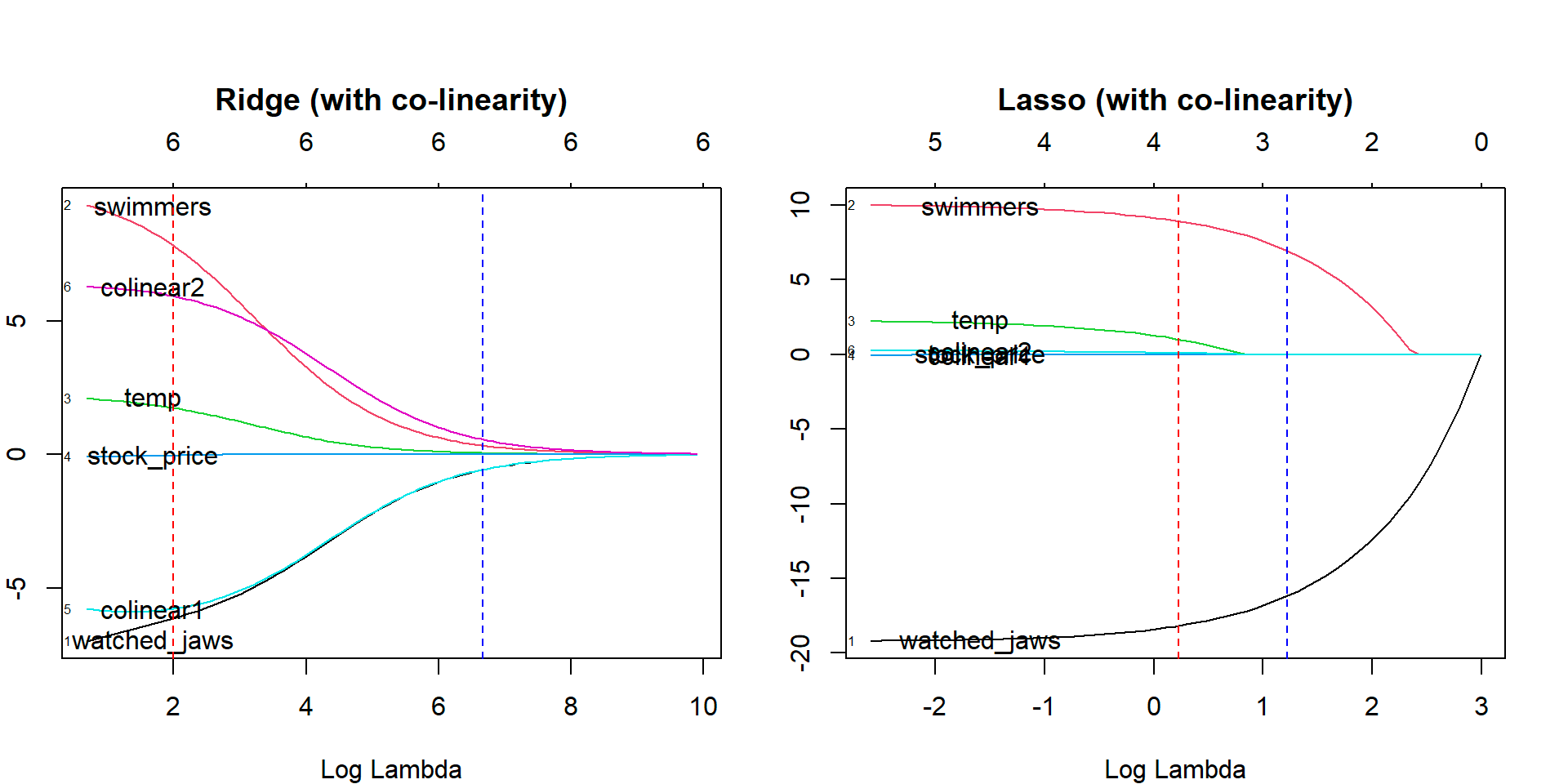
Kaynak

6. Nicel Regresyon

Kuantil regresyon analizi tekniği, lineer regresyon analizinin bir uzantısıdır. Doğrusal regresyon koşulları karşılanmadığında veya verilerde aykırı değerler olduğunda kullanılır. Nicel regresyon, istatistik ve ekonometride uygulamalar bulur.

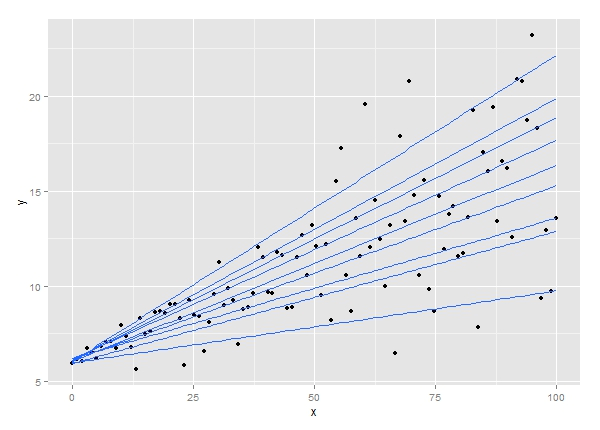
Kaynak

7. Bayes Doğrusal Regresyon

Bayes doğrusal regresyon, makine öğreniminde, regresyon katsayılarının değerini belirlemek için Bayes teoremini kullanan regresyon analizi tekniklerinden biridir. Bu teknik, en küçük kareleri bulmak yerine, özelliklerin sonsal dağılımını belirler. Sonuç olarak, teknik basit doğrusal regresyondan daha fazla kararlılığa sahiptir.

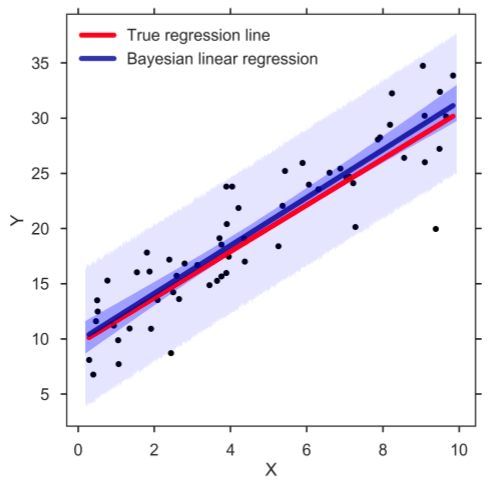
Kaynak

8. Temel Bileşenler Regresyonu

Temel bileşenler regresyon tekniği tipik olarak çoklu bağlantı ile çoklu regresyon verilerini analiz etmek için kullanılır. Sırt regresyon tekniği gibi, ana bileşenler regresyon yöntemi de regresyon tahminlerine bir derece sapma vererek standart hataları en aza indirir. Tekniğin iki adımı vardır - ilk önce eğitim verilerine temel bileşen analizi uygulanır ve ardından dönüştürülmüş örnekler bir regresörü eğitmek için kullanılır.

9. Kısmi En Küçük Kareler Regresyonu

Kısmi en küçük kareler regresyon tekniği, kovaryansa dayalı hızlı ve verimli regresyon analizi tekniklerinden biridir. Bağımsız değişkenlerin sayısının yüksek olduğu ve değişkenler arasında çoklu bağlantının olası olduğu regresyon problemlerinde faydalıdır. Teknik, değişkenleri daha sonra bir regresyon gerçekleştirmek için kullanılan daha küçük bir tahmin kümesine indirger.

10. Elastik Net Regresyon

Elastik net regresyon tekniği, sırt ve kement regresyon modellerinin bir melezidir ve yüksek oranda ilişkili değişkenlerle uğraşırken kullanışlıdır. Regresyon modellerini düzenli hale getirmek için ridge ve lasso regresyon yöntemlerinden alınan cezaları kullanır.

Kaynak

Özet

Burada tartıştığımız regresyon analizi tekniklerinin yanı sıra, makine öğreniminde ekolojik regresyon, adım adım regresyon, jackknife regresyon ve sağlam regresyon gibi birkaç başka regresyon modeli kullanılır. Tüm bu farklı tipteki regresyon tekniklerinin özel kullanım durumu, mevcut verilerin doğasına ve elde edilebilecek doğruluk düzeyine bağlıdır. Genel olarak, regresyon analizinin iki temel faydası vardır. Bunlar aşağıdaki gibidir:

• Bağımlı değişken ile bağımsız değişken arasındaki ilişkiyi gösterir.

• Bağımsız değişkenlerin bağımlı değişken üzerindeki etkisinin gücünü gösterir.

İleriye Doğru: Makine Öğrenimi ve Yapay Zeka alanında Yüksek Lisans Derecesi Kazanın

Bir makine öğrenimi ve yapay zeka kariyerine hazırlanmak için kapsamlı bir çevrimiçi program mı arıyorsunuz?

upGrad, çok yönlü AI uzmanları ve Veri Bilimciler üretmek için Liverpool John Moores Üniversitesi ve IIIT Bangalore ile birlikte Makine Öğrenimi ve Yapay Zeka alanında Yüksek Lisans Derecesi sunar.

Kapsamlı, 20 aylık çevrimiçi program, Derin Öğrenme, NLP, Grafik Modeller, Takviyeli Öğrenme ve benzeri gibi gelişmiş kavram ve becerilerde uzmanlaşmak isteyen çalışan profesyoneller için özel olarak tasarlanmıştır. Ayrıca program, Python, Keras, TensorFlow, Kubernetes, MySQL ve daha fazlası gibi temel programlama dilleri ve araçlarıyla birlikte istatistikte sağlam bir temel sağlamayı amaçlıyor.

Programın Öne Çıkanları:

• Liverpool John Moores Üniversitesi'nden Yüksek Lisans Derecesi
• IIIT Bangalore'dan Yönetici PGP
• 40'tan fazla canlı oturum, 12'den fazla vaka çalışması ve proje, 11 kodlama ödevi, altı bitirme projesi
• Sektör uzmanlarıyla 25+ mentorluk seansı
• 360 derece kariyer yardımı ve öğrenme desteği
• Eşler arası ağ oluşturma fırsatları

Birinci sınıf bir fakülte, pedagoji, teknoloji ve endüstri uzmanları ile upGrad, Güney Asya'nın en büyük yüksek EdTech platformu olarak ortaya çıktı ve dünya çapında 500.000'den fazla çalışan profesyoneli etkiledi. Bugün kaydolun 80'den fazla ülkede upGrad'ın 40.000'den fazla küresel öğrenci tabanının bir parçası olmak için!