Bayes İstatistikleri ve Modeli: Açıklama

Bayes tekniği, veri analizi ve parametre tahmininde kullanılan istatistikte bir yaklaşımdır. Bu yaklaşım Bayes teoremine dayanmaktadır.

Bayes İstatistikleri, istatistiksel bir model kullanarak gözlenen ve gözlemlenmeyen parametreler için ortak olasılık dağılımının belirlenmesine yardımcı olan benzersiz bir ilkeyi takip eder. Bu senaryoda analitik problemlerin üstesinden gelmek için istatistik bilgisi esastır.

Bayes teoremi 1770'lerde Thomas Bayes tarafından tanıtıldığından beri, istatistikte vazgeçilmez bir araç olarak kaldı. Bayes modelleri, istatistiklerdeki son yenilikler tıbbi araştırma, web aramalarını anlama ve doğal dilleri işleme (Doğal Dil İşleme) dahil olmak üzere çok çeşitli endüstrilerde kilometre taşlarının kırılmasına yardımcı olduğundan, sık kullanılan modellerin klasik bir alternatifidir.

Örneğin Alzheimer, kişi yaşlandıkça ilerleyici bir risk oluşturduğu bilinen bir hastalıktır. Ancak, Bayes teoreminin yardımıyla doktorlar, bir kişinin gelecekte Alzheimer olma olasılığını tahmin edebilir. Aynı zamanda, bir kişinin yaşamının sonraki yıllarında savunmasız hale geldiği kanser ve diğer yaşa bağlı hastalıklar için de geçerlidir.

Sık İstatistikler ve Bayes İstatistikleri

Sık İstatistikler ve Bayes istatistikleri, ikisi arasında seçim yapmakta zorluk çeken yeni başlayanlar için sürekli olarak bir tartışma konusu ve kabus olmuştur. 20. yüzyılın başlarında, Bayes istatistikleri, güvensizlik ve kabul konularından payını aldı. Ancak zamanla insanlar Bayes modellerinin uygulanabilirliğini ve sağladığı doğru çözümleri fark ettiler.

Sık istatistiklere ve bunlarla ilişkili karmaşıklıklara bir göz atalım:

Sık İstatistikler

İstatistik dünyasında yaygın olarak kullanılan bir çıkarımsal metodolojidir. Bir olayın (hipotez olarak bahsedilen) olup olmadığını analiz eder. Ayrıca, deneyin süresi boyunca meydana gelen olayın olasılığını da tahmin eder. İstenen sonuç elde edilene kadar deney tekrarlanır.

Dağılım örnekleri gerçek boyuttadır ve deney teorik olarak sonsuz kez tekrarlanır. İşte bir madeni paranın havaya atılmasını incelemek için istatistiklerin ne sıklıkta kullanılabileceğini gösteren bir örnek.

• Yazı tura atıldığında tura gelme olasılığı 0,5 (1/2)'dir.
• Kafa sayısı, elde edilen gerçek potansiyel müşteri sayısını belirtir.
• Gerçek tura sayısı ile beklenen tura sayısı arasındaki fark, atış sayısı arttıkça artacaktır.

Yani burada sonuç, deneyin tekrarlanma sayısına bağlıdır. Sık kullanılan istatistiklerin önemli bir dezavantajıdır.

Tasarım ve yorumlama teknikleriyle ilgili diğer kusurlar, sık istatistiklerin sayısal modellere uygulanmasının zirvede olduğu 20. yüzyılda ortaya çıktı.

Sık İstatistiklerin Sınırlamaları

Sık kullanılan istatistiklerin üç ana kusuru aşağıda listelenmiştir:

1. Değişken p Değerleri

Son nokta ve numune boyutundaki herhangi bir değişiklikle birlikte, tanımlanmış bir son nokta değişikliği olan bir deneyde sabit boyutlu bir numune için ölçülen p değerleri. Tek bir veri için yanlış olan iki p değeriyle sonuçlanır.

2. Tutarsız Güven Aralıkları

CI (Güven Aralığı) yalnızca numune boyutuna bağlıdır. Durma potansiyelini önemsiz hale getirir.

3. Tahmini CI Değerleri

Güven aralıkları bir olasılık dağılımı değildir ve bir parametreye ilişkin değerleri yalnızca bir tahmindir ve gerçek değerler değildir.

Yukarıdaki üç neden, olasılıkları istatistiksel problemlere uygulayan Bayes yaklaşımını doğurdu.

Bayes İstatistiklerinin Doğuşu

Rahip Thomas Bayes ilk olarak 1763'te yazdığı makalesinde istatistiklere Bayesci yaklaşımı önerdi. Bu yaklaşım Richard Price tarafından geçmişe dayalı gelecekteki olayları tahmin etmek için ters olasılıkta bir strateji olarak yayınlandı.

Yaklaşım, aşağıda açıklanan Bayes teoremine dayanmaktadır:

Bayes teoremi

Renyi'nin olasılık aksiyomu, A olayının ve B Olayının meydana gelme olasılıklarının bağımlı veya koşullu olduğu koşullu olasılıkları inceler . Temel koşullu olasılık şu şekilde yazılabilir:

B Olayının meydana gelme olasılığı A Olayına bağlıdır.

Yukarıdaki denklem, Bayes teoreminin matematiksel bir ifadesi olan Bayes kuralının temelidir:

Burada ∩ kesişimi ifade eder.

Bayes kuralı şu şekilde yazılabilir:

Bayes kuralı, istatistiksel bir modeldeki belirli bir parametreye ilişkin mevcut bilgilerin toplanan verilerle karşılaştırıldığı ve güncellendiği Bayes istatistiklerinin temelidir.

Arka plan bilgisi, önceki dağılım olarak temsil edilir ve daha sonra, sonsal dağılımı bulmak için bir olabilirlik fonksiyonu olarak gözlemlenen veya toplanan verilerle karşılaştırılır ve incelenir.

Bu sonsal dağılım, gelecekteki olaylar hakkında tahminlerde bulunmak için kullanılır.

Bayes yaklaşımının uygulamaları aşağıdaki parametrelere bağlıdır:

1. Önceki ve veri modelini tanımlama
2. İlgili çıkarımlarda bulunmak
3. Modellerin incelenmesi ve düzenlenmesi

Bayesian Sinir Ağları nedir?

Bayesian Sinir Ağları (BNN'ler), istatistiksel metodolojiyi kullanarak standart ağları genişlettiğinizde ve fazla uydurmayı takip etmek için sonsal çıkarımı değiştirdiğinizde oluşturduğunuz ağlardır. Bayes yaklaşımı olduğu için sinir ağlarının parametreleriyle ilişkili bir olasılık dağılımı vardır.

Serbest veri akışının olmadığı karmaşık sorunları çözmek için kullanılırlar. Bayesian sinir ağları, moleküler biyoloji ve tıbbi teşhis gibi alanlardaki aşırı uyumu kontrol etmeye yardımcı olur.

Bayesian sinir ağlarını kullanan tek bir olasılıktan ziyade bir soruya verilen cevapların bütün bir dağılımını düşünebiliriz. Model seçimini/karşılaştırmasını belirlemenize ve düzenlileştirmeyi içeren sorunları çözmenize yardımcı olurlar.

Bayes istatistikleri, yeni veriler veya bilimsel kanıtlarla ilgili öznel bilgiyi rasyonelleştirmek ve güncellemek için matematiksel araçlar sunar. Sık istatistiksel yaklaşımın aksine, olasılıkların aynı koşullar altında tekrarlanan olayların sıklığına bağlı olduğu varsayımına dayalı olarak çalışır.

Kısacası Bayes tekniği, bireyin varsayım ve kanaatinin bir uzantısıdır. Bayesian modelini daha verimli kılan en önemli yönü, bireylerin aldıkları bilgi türüne göre farklı görüşlere sahip olduğu anlayışıdır.

Bununla birlikte, yeni kanıtlar ve veriler ortaya çıktıkça, bireylerin bir yakınsama noktası, Bayes çıkarımı olur . Bu rasyonel güncelleme, Bayes istatistiklerinin analitik problemler üzerinde daha etkili olmasını sağlayan özel bir özelliğidir.

Burada, bir olayın gerçekleşeceğine dair hiçbir umut olmadığında 0 olasılığı, olayın gerçekleşeceğinden emin olduğunda 1 olasılığı uygulanır. 0 ile 1 arasındaki bir olasılık, diğer potansiyel sonuçlara yer verir.

Modelden daha iyi bir çıkarım elde etmek için Bayes çıkarımına ulaşmak için artık Bayes kuralı uygulanmaktadır.

Bayes Çıkarımını Elde Etmek için Bayes Kuralını nasıl uygularsınız?

Denklemi düşünün:

P(θ|D) = P(D|θ.)P(θ) / P(D)

P(θ) önceki dağılımı ifade eder,

P(θ|D) sonraki inancı ifade eder,

P(D) kanıtı temsil eder,

P(D|θ) olasılığı gösterir.

Bayes çıkarımının temel amacı, güncellenmiş sonsal inançları elde etmek için inançları kanıtlarla harmanlamak için rasyonel ve matematiksel olarak doğru bir yöntem sunmaktır. Son inançlar, yeni veriler oluşturulduğunda önceki inançlar olarak kullanılabilir. Böylece Bayes çıkarımı, Bayes kuralı yardımıyla inançların sürekli olarak güncellenmesine yardımcı olur.

Aynı yazı tura örneğini göz önünde bulundurarak, Bayes modeli, prosedürü yeni yazı turaları ile öncekinden sonraki inançlara günceller. Bayes yöntemi aşağıdaki olasılıkları verir.

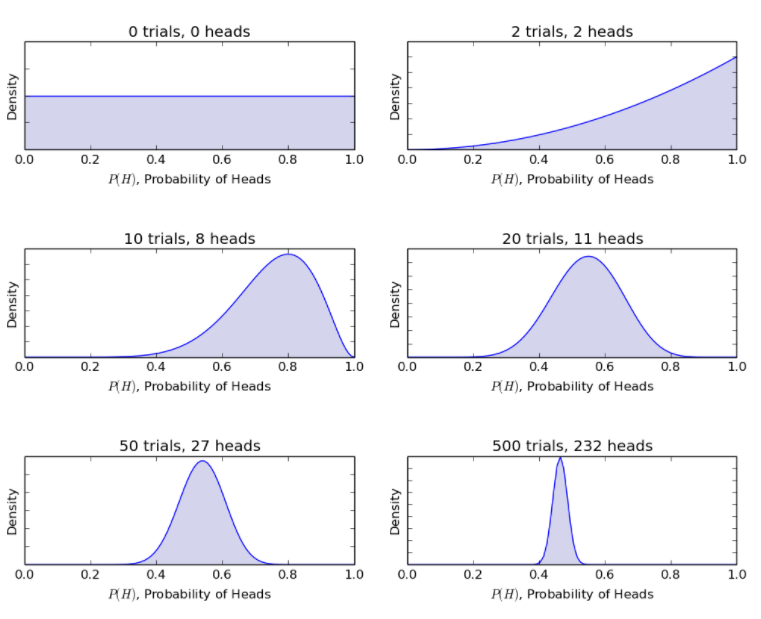
Kaynak

Böylece, Bayes modeli, sınırlı bilgi içeren belirsiz bir senaryoyu, önemli miktarda veri içeren daha tanımlanmış bir senaryoya rasyonalize etmeye izin verir.

Bayes Modeli ile Frequentist Model Arasındaki Önemli Farklar

sık istatistikler

Bayes istatistikleri

Hedef, nokta tahmini olarak kabul edilir ve CI

Hedef, bir sonraki dağılım olarak kabul edilir

Prosedür gözlemlerden başlar

Süreç önceki dağıtımdan başlar

Ne zaman yeni gözlemler yapılsa, frekans yaklaşımı mevcut modeli yeniden hesaplar.

Ne zaman yeni gözlemler yapılsa, sonsal dağılım (ideoloji/hipotez) güncellenir.

Örnekler: Ortalama tahmini, t-testi ve ANOVA.

Örnekler: Ortalamanın sonsal dağılımının tahmini ve yüksek yoğunluklu aralıkların örtüşmesi.

Bayes İstatistiklerinin Avantajları

• Önceden tasarlanmış bilgileri sağlam bir çerçeveyle bilimsel kanıtlarla harmanlamak için organik ve basit bir araç sağlar. Bir parametre hakkındaki geçmiş bilgiler, gelecekteki araştırmalar için bir ön dağılım oluşturmak için kullanılabilir. Çıkarımlar Bayes teoremine bağlıdır.
• Bayes modelinden yapılan çıkarımlar mantıksal ve matematiksel olarak doğrudur ve kaba varsayımlar değildir. Doğruluk, numunenin boyutundan bağımsız olarak sabit kalır.
• Bayes istatistikleri olabilirlik ilkesini takip eder. İki farklı örnek bir inanç θ için ortak olabilirlik fonksiyonuna sahip olduğunda, inançla ilgili tüm çıkarımlar benzer olmalıdır. Klasik istatistiksel teknikler, olabilirlik ilkesini takip etmez.
• Bayes analizinden elde edilen çözümler kolayca yorumlanabilir.
• Hiyerarşik modeller ve eksik veri sorunları gibi çeşitli modeller için elverişli bir platform sunar. Tüm parametrik modellerin hesaplamaları, diğer sayısal tekniklerin yardımıyla sanal olarak izlenebilir.

Bayes Modellerinin Tarih Boyunca Başarılı Uygulamaları

Bayes yöntemleri, II. Dünya Savaşı sırasında birçok başarılı uygulamaya sahipti. Bunlardan birkaçı aşağıda listelenmiştir:

• Rus istatistikçi Andrey Kolmogorov , Rus topçusunun verimliliğini artırmak için Bayes yöntemlerini başarıyla kullandı.
• Alman U teknelerinin kodlarını kırmak için Bayes modelleri kullanıldı.
• Fransız doğumlu Amerikalı matematikçi Bernard Koopman, radyo yayınlarını kesmek için Bayes modellerinin yardımıyla müttefiklerin Alman U teknelerinin yerini belirlemelerine yardımcı oldu.

Bayes istatistikleri hakkında daha fazla bilgi edinmek istiyorsanız, gerçek hayattaki endüstri projeleri ve vaka çalışmaları yoluyla temel kavramları anlamak için upGrad'ın Makine Öğrenimi ve Bulutta Gelişmiş Sertifikası burada. 12 aylık kurs, IIT Madras tarafından sunulur ve kendi hızınızda öğrenmeyi destekler.

Daha fazla ayrıntı için bize ulaşın.