Makine Öğreniminde Bayes Teoremi: Giriş, Nasıl Uygulanır ve Örnek
Yayınlanan: 2021-02-04İçindekiler
Giriş: Bayes Teoremi Nedir?
Bayes Teoremi, olasılıkları içeren matematik alanı olan karar teorisinde yoğun olarak çalışan İngiliz matematikçi Thomas Bayes'in adını almıştır. Bayes Teoremi, sınıfları kesinlik ve doğrulukla tahmin etmenin basit ve etkili bir yolu olduğu makine öğreniminde de yaygın olarak kullanılmaktadır. Bayesian koşullu olasılıkları hesaplama yöntemi, sınıflandırma görevlerini içeren makine öğrenimi uygulamalarında kullanılır.
Naive Bayes Sınıflandırması olarak bilinen Bayes Teoreminin basitleştirilmiş bir versiyonu, hesaplama süresini ve maliyetlerini azaltmak için kullanılır. Bu yazıda sizi bu kavramlara götürüyor ve Bayes Teoreminin makine öğrenimindeki uygulamalarını tartışıyoruz.
Kariyerinizi hızlandırmak için Makine Öğrenimi ve Yapay Zeka alanında Dünyanın en iyi Üniversiteleri - Yüksek Lisanslar, Yönetici Yüksek Lisans Programları ve İleri Düzey Sertifika Programı'ndan çevrimiçi makine öğrenimi kursuna katılın .
Bayes Teoremi Neden Makine Öğreniminde Kullanılır?
Bayes Teoremi, koşullu olasılıkları belirlemek için bir yöntemdir - yani, başka bir olayın zaten gerçekleştiğine göre bir olayın meydana gelme olasılığı. Koşullu olasılık ek koşullar, başka bir deyişle daha fazla veri içerdiğinden, daha doğru sonuçlara katkıda bulunabilir.
Bu nedenle, Makine Öğreniminde doğru tahminlerin ve olasılıkların belirlenmesinde koşullu olasılıklar bir zorunluluktur. Alanın çeşitli alanlarda giderek daha yaygın hale geldiği göz önüne alındığında, Makine Öğreniminde Bayes Teoremi gibi algoritmaların ve yöntemlerin rolünü anlamak önemlidir.
Teoremin kendisine geçmeden önce, bazı terimleri bir örnekle anlayalım. Bir kitapçı yöneticisinin müşterilerinin yaşı ve geliri hakkında bilgisi olduğunu varsayalım. Kitap satışlarının müşterilerin üç yaş sınıfına nasıl dağıldığını bilmek istiyor: gençler (18-35), orta yaşlılar (35-60) ve yaşlılar (60+).

Verilerimizi X olarak adlandıralım. Bayes terminolojisinde X'e kanıt denir. Belirli bir C sınıfına ait bazı X'lerin olduğu bazı H hipotezimiz var.
Amacımız, X, yani P(H | X) verilen H hipotezimizin koşullu olasılığını belirlemektir.
Basit bir ifadeyle, P(H | X) değerini belirleyerek, X verildiğinde X'in C sınıfına ait olma olasılığını elde ederiz. X'in yaş ve gelir nitelikleri vardır – örneğin, 26 yaşında ve 2000$ geliri varsayalım. H, müşterinin kitabı satın alacağı hipotezimizdir.
Aşağıdaki dört terime çok dikkat edin:
- Kanıt – Daha önce tartışıldığı gibi, P(X) kanıt olarak bilinir. Basitçe, bu durumda müşterinin 26 yaşında ve 2000$ kazanıyor olma olasılığıdır.
- Ön Olasılık – Ön olasılık olarak bilinen P(H), hipotezimizin basit olasılığıdır – yani müşterinin bir kitap satın alacağı. Bu olasılık, yaşa ve gelire dayalı olarak herhangi bir ekstra girdi sağlanmayacaktır. Hesaplama daha az bilgi ile yapıldığından sonuç daha az doğrudur.
- Arka Olasılık – P(H | X) arka olasılık olarak bilinir. Burada P(H | X), müşterinin X verilen bir kitabı (H) satın alma olasılığıdır (26 yaşındadır ve 2000$ kazanır).
- Olabilirlik – P(X | H) olabilirlik olasılığıdır. Bu durumda, müşterinin kitabı satın alacağını bildiğimize göre, olasılık olasılığı, müşterinin 26 yaşında ve 2000$ gelire sahip olma olasılığıdır.
Bunlar göz önüne alındığında, Bayes Teoremi şunları belirtir:
P(H | X) = [ P(X | H) * P(H) ] / P(X)
Teoremde yukarıdaki dört terimin görünümüne dikkat edin – sonsal olasılık, olabilirlik olasılığı, önceki olasılık ve kanıt.
Okuyun: Naive Bayes Açıklaması
Bayes Teoremi Makine Öğreniminde Nasıl Uygulanır?
Bayes Teoreminin basitleştirilmiş bir versiyonu olan Naive Bayes Sınıflandırıcı, verileri çeşitli sınıflara doğruluk ve hızla sınıflandırmak için bir sınıflandırma algoritması olarak kullanılır.
Naive Bayes Sınıflandırıcısının bir sınıflandırma algoritması olarak nasıl uygulanabileceğini görelim.
- Genel bir örnek düşünün: X, 'n' özniteliklerinden oluşan bir vektördür, yani X = {x1, x2, x3, …, xn}.
- Diyelim ki {C1, C2, …, Cm} 'm' sınıflarımız var. Sınıflandırıcımız, X'in belirli bir sınıfa ait olduğunu tahmin etmek zorunda kalacak. En yüksek arka olasılığı veren sınıf, en iyi sınıf olarak seçilecektir. Yani matematiksel olarak, sınıflandırıcı Ci iff P(Ci | X) > P(Cj | X) sınıfı için tahminde bulunacaktır. Bayes Teoreminin Uygulanması:
P(Ci | X) = [ P(X | Ci) * P(Ci) ] / P(X)
- P(X) koşuldan bağımsız olduğundan her sınıf için sabittir. Yani P(Ci | X) maksimize etmek için [P(X | Ci) * P(Ci)] maksimize etmeliyiz. Her sınıfın eşit derecede olası olduğunu düşünürsek, elimizde P(C1) = P(C2) = P(C3) … = P(Cn) var. Sonuç olarak, sadece P(X | Ci) maksimize etmemiz gerekiyor.
- Tipik büyük veri kümesinin birkaç özniteliği olması muhtemel olduğundan, her bir öznitelik için P(X | Ci) işlemini gerçekleştirmek hesaplama açısından pahalıdır. Sorunu basitleştirmek ve hesaplama maliyetlerini azaltmak için sınıf koşullu bağımsızlığın geldiği yer burasıdır. Sınıf koşullu bağımsızlık ile, özniteliğin değerlerinin koşullu olarak birbirinden bağımsız olduğunu düşündüğümüzü kastediyoruz. Bu Naive Bayes Sınıflandırmasıdır.
P(Xi | C) = P(x1 | C) * P(x2 | C) *… * P(xn | C)
Daha küçük olasılıkları hesaplamak artık çok kolay. Burada dikkat edilmesi gereken önemli bir nokta: xk her özniteliğe ait olduğu için, uğraştığımız özniteliğin kategorik mi yoksa sürekli mi olduğunu da kontrol etmemiz gerekiyor .
- Kategorik bir özelliğimiz varsa , işler daha basittir. Sadece k özniteliği için xk değerinden oluşan Ci sınıfı örneklerinin sayısını sayabilir ve ardından bunu Ci sınıfı örneklerinin sayısına bölebiliriz.
- Sürekli bir özniteliğimiz varsa, normal dağılım fonksiyonumuz olduğunu düşünürsek, aşağıdaki formülü uygularız, ortalama ? ve standart sapma ?:
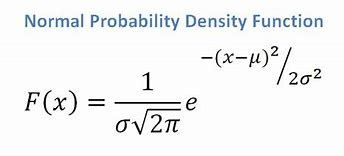

Kaynak
Sonuçta, P(x | Ci) = F(xk, ?k, ?k) elde edeceğiz.
- Şimdi, her Ci sınıfı için Bayes Teoremini kullanmamız gereken tüm değerlere sahibiz. Tahmini sınıfımız, en yüksek olasılığa sahip P(X | Ci) * P(Ci) olan sınıf olacaktır.
Örnek: Bir Kitapevinin Müşterilerini Öngörülü Olarak Sınıflandırma
Bir kitapçıdan aşağıdaki veri setine sahibiz:
| Yaş | Gelir | Öğrenci | Kredi notu | Buys_Book |
| Gençlik | Yüksek | Numara | Adil | Numara |
| Gençlik | Yüksek | Numara | Harika | Numara |
| Orta yaşlı | Yüksek | Numara | Adil | Evet |
| Kıdemli | Orta | Numara | Adil | Evet |
| Kıdemli | Düşük | Evet | Adil | Evet |
| Kıdemli | Düşük | Evet | Harika | Numara |
| Orta yaşlı | Düşük | Evet | Harika | Evet |
| Gençlik | Orta | Numara | Adil | Numara |
| Gençlik | Düşük | Evet | Adil | Evet |
| Kıdemli | Orta | Evet | Adil | Evet |
| Gençlik | Orta | Evet | Harika | Evet |
| Orta yaşlı | Orta | Numara | Harika | Evet |
| Orta yaşlı | Yüksek | Evet | Adil | Evet |
| Kıdemli | Orta | Numara | Harika | Numara |
Yaş, gelir, öğrenci ve kredi notu gibi özelliklerimiz var. Buys_book sınıfımız iki sonuca sahiptir: Evet veya Hayır.
Amacımız, aşağıdaki özelliklere göre sınıflandırmaktır:
X = {yaş = genç, öğrenci = evet, gelir = orta, kredi derecelendirmesi = adil}.
Daha önce gösterdiğimiz gibi, P(Ci | X)'i maksimize etmek için i = 1 ve i = 2 için [ P(X | Ci) * P(Ci) ]'yi maksimize etmemiz gerekir.
Dolayısıyla, P(kitap satın alır = evet) = 9/14 = 0.643
P(kitap satın alır = hayır) = 5/14 = 0.357
P(yaş = gençlik | buys_book = evet) = 2/9 = 0,222
P(yaş = genç | buys_book = hayır) =3/5 = 0.600
P(gelir = orta | buys_book = evet) = 4/9 = 0.444
P(gelir = orta | buys_book = hayır) = 2/5 = 0.400
P(öğrenci = evet | buys_book = evet) = 6/9 = 0.667
P(öğrenci = evet | buys_book = hayır) = 1/5 = 0.200
P(credit_rating = adil | buys_book = evet) = 6/9 = 0,667
P(credit_rating = adil | buys_book = hayır) = 2/5 = 0,400
Yukarıda hesaplanan olasılıkları kullanarak,
P(X | buys_book = evet) = 0.222 x 0.444 x 0.667 x 0.667 = 0.044
Benzer şekilde,
P(X | buys_book = hayır) = 0,600 x 0,400 x 0,200 x 0,400 = 0,019
Ci hangi sınıfı maksimum P(X|Ci)*P(Ci) sağlar? Hesaplıyoruz:
P(X | kitap satın alır = evet)* P(kitap satın alır = evet) = 0,044 x 0,643 = 0,028
P(X | kitap satın alır = hayır)* P(kitap satın alır = hayır) = 0,019 x 0,357 = 0,007

Yukarıdaki ikisini karşılaştırarak, 0.028 > 0.007 olduğundan, Naive Bayes Sınıflandırıcısı, yukarıda belirtilen niteliklere sahip müşterinin bir kitap satın alacağını tahmin eder.
Ödeme: Makine Öğrenimi Projesi Fikirleri ve Konuları
Bayes Sınıflandırıcısı İyi Bir Yöntem mi?
Makine öğreniminde Bayes Teoremine dayalı algoritmalar, diğer algoritmalarla karşılaştırılabilir sonuçlar sağlar ve Bayes sınıflandırıcıları genellikle basit, yüksek doğruluklu yöntemler olarak kabul edilir. Bununla birlikte, Bayes sınıflandırıcılarının, tüm durumlarda değil, sınıf koşullu bağımsızlık varsayımının geçerli olduğu durumlarda özellikle uygun olduğunu unutmamak gerekir. Bir başka pratik endişe, tüm olasılık verilerinin elde edilmesinin her zaman mümkün olmayabileceğidir.
Çözüm
Bayes Teoremi, makine öğreniminde, özellikle sınıflandırma tabanlı problemlerde birçok uygulamaya sahiptir. Bu algoritma ailesini makine öğreniminde uygulamak, önceki olasılık ve sonraki olasılık gibi terimlere aşina olmayı gerektirir. Bu yazıda Bayes Teoreminin temellerini, makine öğrenimi problemlerinde kullanımını tartıştık ve bir sınıflandırma örneği üzerinde çalıştık.
Bayes Teoremi, Makine Öğrenimi'ndeki sınıflandırma tabanlı algoritmaların önemli bir parçasını oluşturduğundan, upGrad'ın Makine Öğrenimi ve NLP'deki Gelişmiş Sertifika Programı hakkında daha fazla bilgi edinebilirsiniz . Bu kurs, Makine Öğrenimi ile ilgilenen, 1-1 mentorluk ve çok daha fazlasını sunan çeşitli öğrenciler göz önünde bulundurularak hazırlanmıştır.
Bayes teoremini neden Makine Öğreniminde kullanıyoruz?
Bayes Teoremi, koşullu olasılıkları veya daha önce başka bir olay meydana gelmişse, bir olayın meydana gelme olasılığını hesaplamak için bir yöntemdir. Koşullu bir olasılık, ekstra koşullar, başka bir deyişle daha fazla veri dahil ederek daha doğru sonuçlara yol açabilir. Makine Öğrenmesinde doğru tahmin ve olasılıkları elde etmek için koşullu olasılıklar gereklidir. Alanın çok çeşitli alanlarda artan yaygınlığı göz önüne alındığında, Makine Öğreniminde Bayes Teoremi gibi algoritmaların ve yaklaşımların önemini anlamak çok önemlidir.
Bayesian Sınıflandırıcı iyi bir seçim mi?
Makine öğreniminde, Bayes Teoremine dayalı algoritmalar, diğer yöntemlerle karşılaştırılabilir sonuçlar üretir ve Bayes sınıflandırıcıları, yaygın olarak basit, yüksek doğruluklu yaklaşımlar olarak kabul edilir. Ancak, Bayes sınıflandırıcılarının her koşulda değil, sınıf koşullu bağımsızlık koşulu doğru olduğunda en iyi şekilde kullanıldığını akılda tutmak önemlidir. Diğer bir husus, tüm olabilirlik verilerinin elde edilmesinin her zaman mümkün olmayabileceğidir.
Bayes teoremi pratikte nasıl uygulanabilir?
Bayes teoremi, kendisiyle ilgili olan veya olabilecek yeni kanıtlara dayalı olarak meydana gelme olasılığını hesaplar. Yöntem, yeni bilgilerin doğru olduğu varsayılarak, varsayımsal yeni bilgilerin bir olayın olasılığını nasıl etkilediğini görmek için de kullanılabilir. Örneğin, 52 kartlık bir desteden seçilen tek bir kart alın. Kartın kral olma olasılığı 4 bölü 52 veya 1/13 veya kabaca yüzde 7,69'dur. Destenin dört kral içerdiğini unutmayın. Diyelim ki seçilen kartın bir yüz kartı olduğu ortaya çıktı. Bir destede 12 resimli kart olduğundan, seçilen kartın kral olma olasılığı 4 bölü 12 veya kabaca yüzde 33.3'tür.
