Bayes Teoremi Örnekle Açıklandı - Eksiksiz Kılavuz

Tanıtım

Bayes Teoremi nedir?

Bayes teoremi, sezginin sıklıkla başarısız olduğu koşullu bir olasılığın hesaplanması için kullanılır. Olasılıkta yaygın olarak kullanılmasına rağmen, teorem makine öğrenimi alanında da uygulanmaktadır. Makine öğreniminde kullanımı, bir modelin eğitim veri kümesine uydurulmasını ve sınıflandırma modellerinin geliştirilmesini içerir.

koşullu olasılık nedir?

Koşullu olasılık, genellikle, başka bir olayın meydana gelmesi durumunda bir olayın olasılığı olarak tanımlanır.

• A ve B iki olaysa, koşullu olasılık me, P(A verilen B) veya P(A|B) olarak belirlenir.
• Koşullu olasılık, ortak olasılıktan hesaplanabilir (A | B) = P(A, B) / P(B)

• Koşullu olasılık simetrik değildir; Örneğin P(A | B) != P(B | A)

Koşullu olasılığı hesaplamanın diğer yolları, diğer koşullu olasılığı kullanmayı içerir;

P(A|B) = P(B|A) * P(A) / P(B)

Ters de kullanılır

P(B|A) = P(A|B) * P(B) / P(A)

Bu hesaplama yöntemi, birleşik olasılığı hesaplamanın zor olduğu durumlarda kullanışlıdır. Aksi takdirde, ters koşullu olasılık mevcut olduğunda, bunun üzerinden hesaplama kolaylaşır.

Bu alternatif koşullu olasılık hesaplamasına Bayes Kuralı veya Bayes Teoremi denir. Onu ilk tanımlayan kişinin adı, “Rahip Thomas Bayes”.

Bayes teoreminin formülü

Bayes teoremi, birleşik olasılık mevcut olmadığında koşullu olasılığı hesaplamanın bir yoludur. Bazen paydaya doğrudan erişilemez. Bu gibi durumlarda alternatif hesaplama yöntemi şu şekildedir:

P(B) = P(B|A) * P(A) + P(B|A değil) * P(A değil)

Bu, alternatif bir P(B) hesaplamasını gösteren Bayes teoreminin formülasyonudur.

P(A|B) = P(B|A) * P(A) / P(B|A) * P(A) + P(B|A değil) * P(A değil)

Yukarıdaki formül, paydanın etrafındaki parantezlerle açıklanabilir.

P(A|B) = P(B|A) * P(A) / (P(B|A) * P(A) + P(B|A değil) * P(A değil))

Ayrıca, elimizde P(A) varsa, o zaman P(A değil) şu şekilde hesaplanabilir:

P(A değil) = 1 – P(A)

Benzer şekilde, eğer P(not B|not A) varsa, o zaman P(B|not A) şu şekilde hesaplanabilir:

P(B|A değil) = 1 – P(B|değil A)

Bayes Koşullu Olasılık Teoremi

Bayes Teoremi, isimleri denklemdeki uygulama bağlamına göre verilen birkaç terimden oluşur.

Arka olasılık, P(A|B) sonucunu ifade eder ve önceki olasılık P(A)'yı ifade eder.

• P(A|B): Arka olasılık.
• P(A): Ön olasılık.

Benzer şekilde, P(B|A) ve P(B) olasılık ve kanıt olarak adlandırılır.

• P(B|A): Olasılık.
• P(B): Kanıt.

Bu nedenle, koşullu olasılığın Bayes teoremi şu şekilde yeniden ifade edilebilir:

Arka = Olasılık * Önceki / Kanıt

Duman varken yangın olma olasılığını hesaplamamız gerekirse, aşağıdaki denklem kullanılacaktır:

P(Ateş|Duman) = P(Duman|Ateş) * P(Ateş) / P(Duman)

Burada, P(Ateş) Önceliktir, P(Duman|Ateş) Olasılıktır ve P(Duman) kanıttır.

Bayes teoreminin bir örneği

Bir problemde Bayes teoreminin kullanımını göstermek için bir Bayes teoremi örneği açıklanmıştır.

Sorun

A, B ve C olarak etiketlenmiş üç kutu mevcuttur. Kutuların detayları şöyle:

• A kutusunda 2 kırmızı ve 3 siyah top vardır.
• B Kutusu 3 kırmızı ve 1 siyah top içerir
• C kutusunda 1 kırmızı ve 4 siyah top vardır.

Her üç kutu da aynı olup, alınma olasılıkları eşittir. Buna göre kırmızı topun A kutusundan alınmış olma olasılığı kaçtır?

Çözüm

E kırmızı bir topun alınması olayını ve A, B ve C topun kendi kutularından alınması olayını göstersin. Bu nedenle koşullu olasılık, hesaplanması gereken P(A|E) olacaktır.

Mevcut olasılıklar P(A) = P(B) = P (C) = 1 / 3, çünkü tüm kutuların seçilme olasılığı eşit.

P(E|A) = A kutusundaki kırmızı top sayısı / A kutusundaki toplam top sayısı = 2 / 5

Benzer şekilde, P(E|B) = 3 / 4 ve P(E|C) = 1 / 5

O halde kanıt P(E) = P(E|A)*P(A) + P(E|B)*P(B) + P(E|C)*P(C)

= (2/5) * (1/3) + (3/4) * (1/3) + (1/5) * (1/3) = 0,45

Bu nedenle, P(A|E) = P(E|A) * P(A) / P(E) = (2/5) * (1/3) / 0,45 = 0,296

Bayes Teoremi Örneği

Bayes teoremi, "testler" hakkında verilen bilgilerle bir "olay" olasılığını verir.

• “Olaylar” ve “testler” arasında bir fark vardır. Örneğin, karaciğer hastalığına, yani bir olaya gerçekten sahip olmaktan farklı bir karaciğer hastalığı testi vardır.
• Nadir olaylar daha yüksek bir yanlış pozitif oranına sahip olabilir.

örnek 1

Alkolik olan bir hastanın karaciğer hastalığı olma olasılığı nedir?

Burada “alkolik olmak” karaciğer hastalığı için “test”tir (litmus testinin türü).

• A, yani “hastada karaciğer hastalığı var” olayıdır.

Kliniğin daha önceki kayıtlarına göre, kliniğe giren hastaların %10'unun karaciğer hastalığından muzdarip olduğu belirtiliyor.

Bu nedenle, P(A)=0.10

• B, “Hasta alkoliktir” turnusol testidir.

Kliniğin daha önceki kayıtları, kliniğe giren hastaların %5'inin alkolik olduğunu gösteriyordu.

Bu nedenle, P(B)=0.05

• Ayrıca karaciğer hastalığı tespit edilen hastaların %7'si alkoliktir. Bu, B|A'yı tanımlar: karaciğer hastalığı olan bir hastanın alkolik olma olasılığı %7'dir.

Bayes teoremi formülüne göre ,

P(A|B) = (0.07 * 0.1)/0.05 = 0.14

Dolayısıyla alkolik olan bir hastanın karaciğer hastalığı geçirme olasılığı 0,14 (%14)'dür.

Örnek2

• Tehlikeli yangınlar nadirdir (%1)
• Ancak mangal nedeniyle duman oldukça yaygındır (%10),
• Ve tehlikeli yangınların %90'ı duman çıkarır

Duman varken tehlikeli Yangın olasılığı nedir?

Hesaplama

P(Ateş|Duman) =P(Ateş) P(Duman|Ateş)/P(Duman)

= %1 x %90/10%

= %9

Örnek 3

Gün boyunca yağmur ihtimali nedir? Nerede, Yağmur gün boyunca yağmur anlamına gelir ve Bulut bulutlu sabah anlamına gelir.

Buluta verilen Yağmur ihtimali P(Rain|Cloud) şeklinde yazılır.

P(Yağmur|Bulut) = P(Yağmur) P(Bulut|Yağmur)/P(Bulut)

P(Yağmur) Yağmur Olasılığı = %10

P(Bulut|Yağmur) Bulut Olasılığıdır, Yağmurun meydana gelme olasılığı = %50

P(Bulut) Bulut Olasılığı = %40

P(Yağmur|Bulut) = 0,1 x 0,5/0,4 = 0,125

Bu nedenle, %12,5 yağmur ihtimali.

Uygulamalar

Bayes teoreminin birçok uygulaması gerçek dünyada mevcuttur. Teoremin birkaç ana uygulaması şunlardır:

1. Modelleme Hipotezleri

Bayes teoremi, uygulamalı makine öğreniminde geniş uygulama alanı bulur ve veriler ile model arasında bir ilişki kurar. Uygulamalı makine öğrenimi, belirli bir veri kümesinde farklı hipotezlerin test edilmesi ve analiz edilmesi sürecini kullanır.

Veri ve model arasındaki ilişkiyi açıklamak için Bayes teoremi olasılıksal bir model sağlar.

P(h|D) = P(D|h) * P(h) / P(D)

Neresi,

P(h|D): Hipotezin arka olasılığı

P(h): Hipotezin ön olasılığı.

P(D)'deki bir artış P(h|D)'yi azaltır. Tersine, eğer P(h) ve verilen hipotezi gözlemleme olasılığı artarsa, o zaman P(h|D) olasılığı artar.

2. Sınıflandırma için Bayes Teoremi

Sınıflandırma yöntemi, belirli bir verinin etiketlenmesini içerir. Bir veri örneği verilen bir sınıf etiketinin koşullu olasılığının hesaplanması olarak tanımlanabilir.

P(sınıf|veri) = (P(veri|sınıf) * P(sınıf)) / P(veri)

Burada P(class|data), sağlanan veri verilen sınıfın olasılığıdır.

Hesaplama her sınıf için yapılabilir. En büyük olasılığa sahip sınıf, girdi verilerine atanabilir.

Koşullu olasılığın hesaplanması, az sayıda örneğin koşulları altında mümkün değildir. Bu nedenle, Bayes teoreminin doğrudan uygulaması mümkün değildir. Sınıflandırma modeline bir çözüm basitleştirilmiş hesaplamada yatmaktadır.

• Saf Bayes Sınıflandırıcısı

Bayes teoremi, girdi değişkenlerinin, hesaplama karmaşıklığına neden olan diğer değişkenlere bağlı olduğunu düşünür. Bu nedenle, varsayım kaldırılır ve her girdi değişkeni bağımsız bir değişken olarak kabul edilir. Sonuç olarak, model bağımlıdan bağımsız koşullu olasılık modeline değişir. Sonuçta karmaşıklığı azaltır.

Bayes teoreminin bu basitleştirilmesine Naive Bayes denir. Modelleri sınıflandırmak ve tahmin etmek için yaygın olarak kullanılır.

• Bayes Optimal Sınıflandırıcı

Bu, eğitim veri kümesi verilen yeni bir örneğin tahminini içeren bir tür olasılıklı modeldir. Bayes Optimal Sınıflandırıcının bir örneği, "Eğitim verileri verilen yeni örneğin en olası sınıflandırması nedir?"

Eğitim verisi verilen yeni bir örneğin koşullu olasılığının hesaplanması aşağıdaki denklem ile yapılabilir.

P(vj | D) = toplam {h cinsinden H} P(vj | hi) * P(hi | D)

vj, sınıflandırılacak yeni bir örnek olduğunda,

H, örneği sınıflandırmak için hipotezler kümesidir,

merhaba verilen bir hipotez,

P(vj | hi) hi hipotezi verilen vi için arka olasılıktır ve

P(hi | D), D verisi verilen hi hipotezinin arka olasılığıdır.

3. Bayes teoreminin makine öğreniminde kullanımları

Bayes teoreminin makine öğreniminde en yaygın uygulaması, sınıflandırma problemlerinin geliştirilmesidir. Sınıflandırma dışındaki diğer uygulamalar, optimizasyon ve geçici modelleri içerir.

• Bayes optimizasyonu

Belirli bir amaç fonksiyonunun minimum veya maksimum maliyetiyle sonuçlanan bir girdi bulmak her zaman zor bir iştir. Bayes optimizasyonu, Bayes teoremine dayanır ve global bir optimizasyon probleminin aranması için bir bakış açısı sağlar. Yöntem, olasılıksal bir modelin (vekil fonksiyon) oluşturulmasını, bir toplama fonksiyonunda arama yapılmasını ve gerçek amaç fonksiyonunu değerlendirmek için aday örneklerin seçimini içerir.

Uygulamalı makine öğreniminde, iyi performans gösteren bir modelin hiper parametrelerini ayarlamak için Bayes optimizasyonu kullanılır.

• Bayes İnanç ağları

Değişkenler arasındaki ilişkiler, olasılık modelleri kullanılarak tanımlanabilir. Ayrıca olasılıkların hesaplanmasında da kullanılırlar. Tamamen koşullu bir olasılık modeli, büyük miktarda veri nedeniyle olasılıkları hesaplayamayabilir. Naive Bayes, hesaplama yaklaşımını basitleştirdi. Rastgele değişkenler arasındaki bilinen koşullu bağımlılığa ve diğer durumlarda koşullu bağımsızlığa dayalı olarak bir modelin geliştirildiği başka bir yöntem daha mevcuttur. Bayes ağı, bu bağımlılığı ve bağımsızlığı, yönlendirilmiş kenarlara sahip olasılıklı grafik modeli aracılığıyla gösterir. Bilinen koşullu bağımlılık, yönlendirilmiş kenarlar olarak görüntülenir ve eksik bağlantılar modeldeki koşullu bağımsızlıkları temsil eder.

4. Bayesian Spam filtreleme

Spam filtreleme, Bayes teoreminin başka bir uygulamasıdır. İki olay mevcuttur:

• Olay A: İleti spam.
• Test X: Mesaj belirli kelimeleri içeriyor (X)

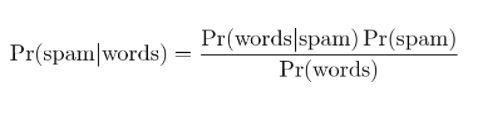
Bayes teoreminin uygulanması ile “test sonuçları” verilerek mesajın spam olup olmadığı tahmin edilebilir. Bir mesajdaki kelimeleri analiz etmek, spam mesajı olma olasılığını hesaplayabilir. Tekrarlanan mesajlarla filtrelerin eğitilmesiyle, mesajda belirli kelimelerin bulunma olasılığının spam olacağı gerçeğini günceller.

Bayes teoreminin bir örnekle uygulaması

Bir katalizör üreticisi, belirli bir elektrokatalizördeki (EC) kusurları test etmek için bir cihaz üretir. Katalizör üreticisi, EC'nin kusurlu olması durumunda testin %97, kusursuz olduğunda ise %99 güvenilir olduğunu iddia ediyor. Ancak, söz konusu EC'nin %4'ünün teslimat sırasında kusurlu olması beklenebilir. Cihazın gerçek güvenilirliğini belirlemek için Bayes kuralı uygulanır. Temel olay kümeleri şunlardır:

A : EC arızalı; A': EC kusursuzdur; B: EC'nin kusurlu olduğu test edilmiştir; B': EC'nin kusursuz olduğu test edilmiştir.

Olasılıklar

B/A: EC'nin (olduğu biliniyor) kusurlu ve test edilmiş kusurlu, P(B/A) = 0.97,

B'/A: EC kusurlu (olduğu biliniyor), ancak kusursuz test edildi, P(B'/A)=1-P(B/A)=0.03,

B/A': EC'nin (olduğu biliniyor) kusurlu, ancak test edilmiş kusurlu, P(B/A') = 1- P(B'/A')=0.01

B'/A: = EC kusursuzdur (olduğu bilinmektedir) ve kusursuz test edilmiştir P(B'/A') = 0.99

Bayes teoremi ile hesaplanan olasılıklar:

Hesaplama olasılığı, kusursuz EC'leri reddetme olasılığının yüksek olduğunu (yaklaşık %20) ve hatalı EC'leri belirleme olasılığının düşük olduğunu (yaklaşık %80) göstermektedir.

Çözüm

Bayes teoreminin en çarpıcı özelliklerinden biri, birkaç olasılık oranından çok büyük miktarda bilgi elde edilebilmesidir. Olabilirlik araçlarıyla, önceki bir olayın olasılığı, sonraki olasılığa dönüştürülebilir. Bayes teoreminin yaklaşımları istatistik, epistemoloji ve tümevarımsal mantık alanlarında uygulanabilir.

Bayes Teoremi, yapay zeka ve makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, IIIT-B & upGrad'ın çalışan profesyoneller için tasarlanmış ve 450+ saatlik zorlu eğitim, 30'dan fazla vaka sunan Makine Öğrenimi ve Yapay Zeka alanında Yönetici PG Programına göz atın çalışmalar ve ödevler, IIIT-B Mezun statüsü, 5'ten fazla pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.