การคิดแบบเบย์คืออะไร? บทนำและทฤษฎีบท

ทฤษฎีบททางสถิติที่กำหนดโดยโธมัส เบย์ส์ นักสถิติและนักปรัชญาชาวอังกฤษในช่วงทศวรรษ 1700 ยังคงเป็นแสงนำทางสำหรับนักวิทยาศาสตร์และนักวิเคราะห์ทั่วโลก ทุกวันนี้ การคิดแบบเบย์พบการประยุกต์ใช้ในด้านการแพทย์ วิทยาศาสตร์ เทคโนโลยี และสาขาวิชาอื่นๆ และยังคงมีอิทธิพลต่อมุมมองโลกทัศน์และการกระทำที่เป็นผลอย่างแข็งขัน

แนวคิดของ Thomas' Bayes นั้นเรียบง่ายมาก จากข้อมูลของ Bayes ความน่าจะเป็นของสมมติฐานที่เป็นจริงนั้นขึ้นอยู่กับสองเงื่อนไข: ความสมเหตุสมผลนั้นขึ้นอยู่กับสิ่งที่เรารู้อยู่แล้ว (ความรู้เดิม) และความเหมาะสมของหลักฐานใหม่มากน้อยเพียงใด ดังนั้น การคิดแบบเบย์จึงแตกต่างจากการทดสอบสมมติฐานแบบเดิมๆ โดยที่วิธีเดิมจะรวมความรู้เดิมไว้ก่อนก่อนที่จะสรุป

เมื่อคำนึงถึงการแนะนำเบื้องต้นแล้ว ให้เราเจาะลึกรายละเอียดเพิ่มเติมเล็กน้อยเกี่ยวกับสถิติแบบเบย์

สถิติเบย์

พูดง่ายๆ ก็คือ สถิติแบบเบย์จะใช้ความน่าจะเป็นกับปัญหาทางสถิติเพื่ออัปเดตความเชื่อก่อนหน้าโดยพิจารณาจากหลักฐานของข้อมูลใหม่ ความน่าจะเป็นแสดงถึงระดับของความเชื่อในเหตุการณ์เฉพาะ

ระดับของความเชื่ออาจขึ้นอยู่กับความรู้ก่อนหน้าเกี่ยวกับเหตุการณ์ตามสมมติฐานส่วนตัวหรือผลการทดลองก่อนหน้า สถิติแบบเบย์ใช้ทฤษฎีบทของเบย์ในการคำนวณความน่าจะเป็น ในทางกลับกัน ทฤษฎีบทของเบย์จะอธิบายความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์โดยอิงจากหลักฐานใหม่และข้อมูลก่อนหน้าที่เกี่ยวข้องกับเหตุการณ์

โดยคำนึงถึงสิ่งนั้น ให้เราทบทวนแนวคิดพื้นฐานของความน่าจะเป็นแบบมีเงื่อนไขก่อนที่เราจะเข้าใจทฤษฎีบทของเบย์ในเชิงลึก

ความน่าจะเป็นแบบมีเงื่อนไข

ความน่าจะเป็นแบบมีเงื่อนไขสามารถกำหนดเป็นความน่าจะเป็นของเหตุการณ์หรือผลลัพธ์โดยพิจารณาจากเหตุการณ์หรือผลลัพธ์ก่อนหน้า คำนวณโดยการคูณความน่าจะเป็นของเหตุการณ์ก่อนหน้าด้วยความน่าจะเป็นของเหตุการณ์ที่ตามมาหรือเหตุการณ์ตามเงื่อนไข

มาดูตัวอย่างเพื่อทำความเข้าใจแนวคิดกันดีกว่า

• เหตุการณ์ A คือครอบครัวที่วางแผนจะไปเที่ยวปิกนิก มีโอกาส 80% ที่ครอบครัวจะไปปิกนิก
• เหตุการณ์ B คือวันที่ฝนตกในวันที่ครอบครัวออกไปปิกนิก พยากรณ์อากาศบอกว่ามีโอกาส 60% ที่ฝนจะตกในวันปิกนิก
• ดังนั้น ความน่าจะเป็น (P) ที่ครอบครัวไปปิกนิกและฝนตกจึงคำนวณได้ดังนี้

P (ปิกนิกและฝน) = P (ฝน | ปิกนิก) P (ปิกนิก) = (0.60) * (0.80) = 0.48

ในตัวอย่างข้างต้น ความน่าจะเป็นแบบมีเงื่อนไขจะพิจารณาเหตุการณ์สองเหตุการณ์ A และ B ที่มีความสัมพันธ์ซึ่งกันและกัน นั่นคือ ความน่าจะเป็นที่ครอบครัวจะไปปิกนิกและฝนก็ตกในวันเดียวกันด้วย

ดังนั้น ความน่าจะเป็นแบบมีเงื่อนไขจึงแตกต่างจากความน่าจะเป็นแบบไม่มีเงื่อนไข เนื่องจากความน่าจะเป็นแบบหลังหมายถึงความน่าจะเป็นของการเกิดเหตุการณ์โดยไม่คำนึงว่าเหตุการณ์หรือเหตุการณ์อื่นเกิดขึ้นหรือมีเงื่อนไขอื่นใดอยู่

สูตรความน่าจะเป็นแบบมีเงื่อนไข

สูตรความน่าจะเป็นแบบมีเงื่อนไขมาจากกฎการคูณความน่าจะเป็น:

P (A และ B) หรือ P (AUB) = P ( B ให้ A) หรือ P (B | A) * P (A)

ในสมการข้างต้น P (A และ B) คือความน่าจะเป็นร่วมกัน ซึ่งหมายถึงความน่าจะเป็นที่เหตุการณ์สองเหตุการณ์ขึ้นไปเกิดขึ้นพร้อมกัน เขียนเป็น P (A,B) ด้วย

ต่อไปนี้เป็นวิธีอนุมานสมการความน่าจะเป็นแบบมีเงื่อนไขจากกฎการคูณ:

ขั้นตอนที่ 1: เขียนกฎการคูณ

P (A และ B) = P (B | A) * P (A)

ขั้นตอนที่ 2: หารทั้งสองข้างของสมการด้วย P (A)

P (A และ B) / P (A) = P (B | A) * P (A) / P (A)

ขั้นตอนที่ 3: ยกเลิก P (A) ทางด้านขวาของสมการ

P (A และ B) / P (A) = P (B | A)

ขั้นตอนที่ 4: เขียนสมการใหม่

P (A และ B) = P (B | A) / P (A)

ดังนั้น สูตรของความน่าจะเป็นแบบมีเงื่อนไขจึงถูกกำหนดเป็น:

P (A และ B) = P (B | A) / P (A)

ทฤษฎีบทของเบย์

เมื่อใช้ทฤษฎีบทของเบย์ส์ เราสามารถอัปเดตความเชื่อและความเชื่อมั่นของเราตามหลักฐานใหม่และที่เกี่ยวข้อง ตัวอย่างเช่น หากเรากำลังพยายามหาความน่าจะเป็นของคนที่เป็นมะเร็ง โดยทั่วไปเราจะถือว่ามันเป็นเปอร์เซ็นต์ของประชากรที่เป็นมะเร็ง อย่างไรก็ตาม หากเรานำเสนอหลักฐานเพิ่มเติม เช่น บุคคลที่เป็นปัญหาเป็นผู้สูบบุหรี่ เราสามารถปรับปรุงการรับรู้ของเรา (และด้วยเหตุนี้ความน่าจะเป็น) เนื่องจากความน่าจะเป็นที่จะเป็นมะเร็งจะสูงขึ้นหากบุคคลนั้นสูบบุหรี่ ดังนั้นเราจึงใช้ทั้งความรู้เดิมของเราและหลักฐานเพิ่มเติมเพื่อปรับปรุงการประมาณการของเรา

สูตรสำหรับทฤษฎีบทเบย์

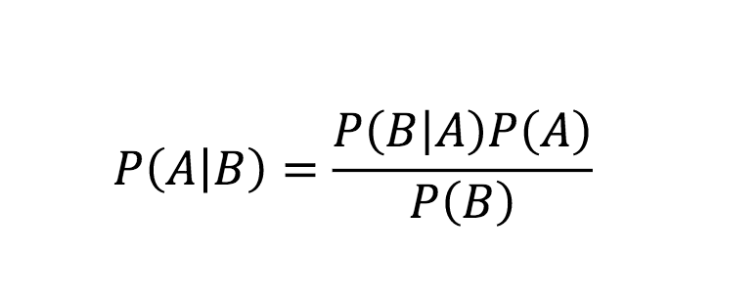
แหล่งที่มา

สมการข้างต้นเป็นกฎของเบย์ ทีนี้ ให้เรามาดูที่มาแบบเป็นขั้นของสมการทฤษฎีบทเบย์กัน

ขั้นตอนที่ 1: พิจารณาสองเหตุการณ์ A และ B. A เป็นเหตุการณ์ที่มีความน่าจะเป็นที่เราต้องการคำนวณและ B เป็นหลักฐานเพิ่มเติมที่เกี่ยวข้องกับ A

ขั้นตอนที่ 2: เขียนความสัมพันธ์ระหว่างความน่าจะเป็นร่วมและความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ A และ B

P (A,B) = P (A | B) * P(B) = P (B,A) = P (B | A) * P(A)

ขั้นตอนที่ 3: ตั้งค่าเงื่อนไขความน่าจะเป็นแบบมีเงื่อนไขสองเงื่อนไขให้เท่ากัน

P (A | B) * P(B) = P (B | A) * P(A)

ขั้นตอนที่ 4: หารทั้งสองข้างของสมการด้วย P (B)

P (A | B) * P(B) / P (B) = P (B | A) * P(A) / P (B)

ขั้นตอนที่ 5: ยกเลิก P (B) ทางด้านซ้ายของสมการ

P (A | B) = P (B | A) * P(A) / P (B)

ดังนั้นเราจึงได้สูตรของทฤษฎีบทเบย์ดังนี้:

P (A | B) = P (B | A) * P(A) / P (B)

การทำความเข้าใจเงื่อนไขในสมการทฤษฎีบทของเบย์

P (A | B) = P (B | A) * P(A) / P (B)

• P (A | B) เรียกว่า ความน่าจะเป็น หลัง หรือความน่าจะเป็นที่เราพยายามจะประมาณ จากตัวอย่างก่อนหน้านี้ ความน่าจะเป็นภายหลังคือความน่าจะเป็นของผู้ที่เป็นมะเร็ง เนื่องจากบุคคลนั้นสูบบุหรี่เป็นประจำ
• P (B | A) เรียกว่าความ น่าจะ เป็น ซึ่งหมายถึงความน่าจะเป็นที่จะตรวจพบหลักฐานเพิ่มเติม จากสมมติฐานเบื้องต้นของเรา ในตัวอย่างข้างต้น ความน่าจะเป็นคือความน่าจะเป็นของผู้สูบบุหรี่ เนื่องจากบุคคลนั้นเป็นมะเร็ง
• P (A) คือ ความน่าจะเป็น ก่อนหน้า หรือความน่าจะเป็นของสมมติฐานของเราโดยไม่มีหลักฐานหรือข้อมูลเพิ่มเติม ในตัวอย่างข้างต้น ความน่าจะเป็นก่อนหน้าคือความน่าจะเป็นที่จะเป็นมะเร็ง
• P (B) คือความ น่าจะ เป็นส่วนเพิ่ม หรือความน่าจะเป็นรวมของการสังเกตหลักฐาน ในบริบทของตัวอย่างข้างต้น ความน่าจะเป็นส่วนเพิ่มคือความน่าจะเป็นที่จะเป็นผู้สูบบุหรี่

ตัวอย่างง่ายๆ เพื่อทำความเข้าใจทฤษฎีบทของเบย์

ในตัวอย่างที่แล้ว เราจะเห็นผลของการใช้ทฤษฎีบทของเบย์โดยใช้ตัวเลขสมมุติฐานบางส่วน

สมมติว่าความน่าจะเป็นที่จะเป็นมะเร็งเท่ากับ 0.06 นั่นคือ 6% ของคนเป็นมะเร็ง สมมติว่าความน่าจะเป็นของการสูบบุหรี่คือ 0.20 หรือ 20% ของผู้สูบบุหรี่ และ 30% ของผู้ที่เป็นมะเร็งเป็นผู้สูบบุหรี่ ดังนั้น พี (ผู้สูบบุหรี่ | มะเร็ง) = 0.30 น.

ในขั้นต้น ความน่าจะเป็นที่จะเป็นมะเร็งนั้นอยู่ที่ 0.06 (ก่อนหน้า) แต่จากหลักฐานใหม่เราสามารถคำนวณ P (Cancer | Smoker) = P ((Smoker | Cancer) * P (Cancer)) / P (Smoker) = (0.30*0.06) / (0.20) = 0.09

เรียนรู้ หลักสูตรวิทยาศาสตร์ข้อมูล ออนไลน์จากมหาวิทยาลัยชั้นนำของโลก รับโปรแกรม PG สำหรับผู้บริหาร โปรแกรมประกาศนียบัตรขั้นสูง หรือโปรแกรมปริญญาโท เพื่อติดตามอาชีพของคุณอย่างรวดเร็ว

ก้าวไปข้างหน้า: ฝึกฝนแนวคิดของสถิติสำหรับอาชีพใน Data Science หรือ Machine Learning

แพลตฟอร์มการเรียนรู้ EdTech ที่สูงขึ้นของ upGrad ได้ส่งผลกระทบต่อคนทำงานกว่า 500,000 คนทั่วโลกด้วยหลักสูตรมากมายและประสบการณ์การเรียนรู้ที่สมจริง ด้วยฐานผู้เรียนมากกว่า 40,000 รายในกว่า 85 ประเทศ หลักสูตรที่เกี่ยวข้องกับอุตสาหกรรมของ upGrad รับประกันความก้าวหน้าในอาชีพของคุณในสาขาที่คุณเลือก

วิทยาศาสตรมหาบัณฑิตสาขาวิทยาศาสตร์ข้อมูล เป็นหลักสูตรระยะเวลา 18 เดือนที่สอนทักษะที่สำคัญในด้านสถิติ การวิเคราะห์เชิงทำนาย การเรียนรู้ของเครื่อง การวิเคราะห์ข้อมูลขนาดใหญ่ การแสดงข้อมูล เป็นต้น

ไฮไลท์ของโปรแกรม:

• ปริญญาโทจาก Liverpool John Moores University และ Executive PGP จาก IIIT Bangalore
• เนื้อหามากกว่า 500 ชั่วโมง กรณีศึกษาและโครงการมากกว่า 60 รายการ เซสชันสดมากกว่า 20 รายการ ภาษาและเครื่องมือการเขียนโปรแกรม 14+
• เครือข่ายอุตสาหกรรม เซสชันการแก้ปัญหาข้อสงสัย และการสนับสนุนการเรียนรู้

โปรแกรมประกาศนียบัตรขั้นสูงในการเรียนรู้ของเครื่องและการเรียนรู้เชิงลึก เป็นหลักสูตร 6 เดือนที่เข้มงวดพร้อมโอกาสในการสร้างเครือข่ายแบบเพื่อน โครงการภาคปฏิบัติ การให้คำปรึกษาในอุตสาหกรรม และความช่วยเหลือด้านอาชีพแบบ 360 องศา

ไฮไลท์ของโปรแกรม:

• การยอมรับอันทรงเกียรติจาก IIIT Bangalore
• เนื้อหามากกว่า 240 ชั่วโมง กรณีศึกษาและโครงการมากกว่า 5 รายการ เซสชันสดมากกว่า 24 รายการ ครอบคลุมภาษาโปรแกรม เครื่องมือ และห้องสมุด 12 ภาษา
• เซสชั่นการฝึกสอนแบบกลุ่ม 1:8 และเซสชั่นการให้คำปรึกษาแบบ 1:1 กับผู้เชี่ยวชาญในอุตสาหกรรม

บทสรุป

การคิดแบบเบย์สนับสนุนการคิด การไต่ถาม และความเชื่อหลายๆ ด้านของมนุษย์ แม้ว่าพวกเราส่วนใหญ่จะไม่ทราบเรื่องนี้ก็ตาม ตั้งแต่ การตรวจคัดกรองมะเร็ง และ ภาวะโลกร้อน ไปจนถึง นโยบายการเงิน การ ประเมินความเสี่ยงและการประกันภัย การ คิดแบบเบย์เป็นพื้นฐาน แม้แต่นักคณิตศาสตร์ชาวอังกฤษชื่อดังอย่าง อลัน ทัวริง ก็เชื่อกันว่าใช้วิธีเบย์เซียนในการถอดรหัสอีนิกมาของเยอรมันในช่วงสงครามโลกครั้งที่สอง

ลงทะเบียนกับ upGrad และเรียนรู้เพิ่มเติมเกี่ยวกับแนวคิดทางสถิติที่สำคัญ และอีกมากมาย!