เริ่มต้นกับการถดถอยทวินามลบ: คำแนะนำทีละขั้นตอน

เทคนิคการถดถอยทวินามเชิงลบใช้สำหรับการสร้างแบบจำลองของตัวแปรนับ วิธีการนี้เกือบจะคล้ายกับวิธีการถดถอยพหุคูณ อย่างไรก็ตาม มีความแตกต่างที่ในกรณีของการถดถอยทวินามเชิงลบ ตัวแปรตาม เช่น Y จะตามหลังการแจกแจงทวินามลบ ดังนั้น ค่าของตัวแปรอาจเป็นจำนวนเต็มที่ไม่ติดลบ เช่น 0, 1, 2

วิธีการนี้ยังเป็นส่วนเสริมของการถดถอยแบบปัวซองที่ทำให้ผ่อนคลายโดยสมมติว่าค่าเฉลี่ยเท่ากับความแปรปรวน หนึ่งในแบบจำลองดั้งเดิมของการถดถอยทวินาม ซึ่งกำหนดเป็น “NB2” นั้นอิงจากการแจกแจงแบบผสมของปัวซอง-แกมมา

วิธีการถดถอยปัวซองเป็นแบบทั่วไปโดยการเพิ่มตัวแปรของสัญญาณรบกวนแกมมา ตัวแปรนี้มีค่าเท่ากับหนึ่งและพารามิเตอร์มาตราส่วนคือ "v"

ต่อไปนี้คือตัวอย่างบางส่วนของการถดถอยทวินามเชิงลบ:

• ผู้บริหารโรงเรียนได้ทำการศึกษาเพื่อศึกษาพฤติกรรมการเข้าชั้นเรียนของนักเรียนชั้นมัธยมศึกษาตอนปลายจากสองโรงเรียน ปัจจัยที่อาจส่งผลต่อพฤติกรรมการเข้าชั้นเรียนอาจรวมถึงวันที่รุ่นน้องขาดเรียน นอกจากนี้โปรแกรมที่พวกเขาลงทะเบียน
• นักวิจัยจากการศึกษาเกี่ยวกับสุขภาพได้ทำการศึกษาจำนวนผู้สูงอายุที่ไปโรงพยาบาลในช่วง 12 เดือนที่ผ่านมา การศึกษานี้พิจารณาจากลักษณะเฉพาะของแต่ละบุคคลและแผนสุขภาพที่ผู้สูงอายุซื้อ

ตัวอย่างของการถดถอยทวินามลบ

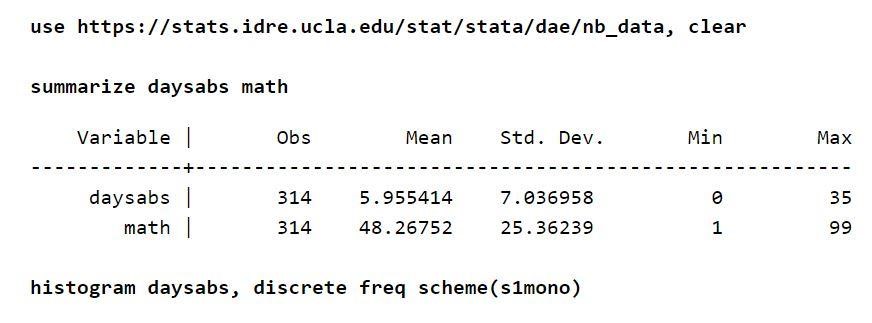
สมมติว่ามีใบตอบรับนักเรียนประมาณ 314 คนจากโรงเรียนมัธยมศึกษาตอนปลาย ข้อมูลนำมาจากโรงเรียนในเมืองสองแห่งและจัดเก็บไว้ในไฟล์ชื่อ nb_data.dta ตัวแปรตอบสนองที่น่าสนใจในตัวอย่างนี้คือวันที่ขาดหายไปซึ่งก็คือ “daysabs” มีตัวแปรหนึ่งตัวคือ "คณิตศาสตร์" ซึ่งกำหนดคะแนนคณิตศาสตร์สำหรับนักเรียนทุกคน มีตัวแปรอื่นซึ่งก็คือ "prog" ตัวแปรนี้ระบุโปรแกรมที่นักเรียนลงทะเบียน

แหล่งที่มา

ตัวแปรแต่ละตัวมีข้อสังเกตประมาณ 314 รายการ ดังนั้นการแจกแจงระหว่างตัวแปรก็สมเหตุสมผลเช่นกัน นอกจากนี้ เมื่อพิจารณาตัวแปรผลลัพธ์แล้ว ค่าเฉลี่ยแบบไม่มีเงื่อนไขจะต่ำกว่าค่าความแปรปรวน

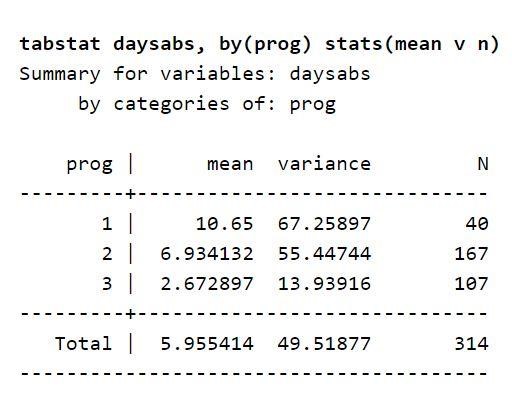
ตอนนี้ ให้เน้นที่คำอธิบายตัวแปรที่พิจารณาในชุดข้อมูล ตารางแสดงจำนวนวันเฉลี่ยที่นักเรียนขาดเรียนในโปรแกรมทุกประเภท นี่แสดงให้เห็นว่าโปรแกรมประเภทตัวแปรสามารถทำนายวันที่นักเรียนขาดเรียนได้ คุณยังสามารถใช้เพื่อทำนายตัวแปรผลลัพธ์ได้อีกด้วย เนื่องจากค่ากลางของตัวแปรผลลัพธ์จะแตกต่างกันไปตามตัวแปรที่โปรก นอกจากนี้ ค่าของความแปรปรวนจะสูงกว่าค่าในแต่ละระดับของตัวแปร prog ค่าเหล่านี้เรียกว่าความแปรปรวนและวิธีการ ความแตกต่างที่มีอยู่ชี้ให้เห็นว่ามีการกระจายตัวมากเกินไป ดังนั้น จึงเหมาะสมที่จะใช้แบบจำลองทวินามเชิงลบ

แหล่งที่มา

นักวิจัยสามารถพิจารณาวิธีการวิเคราะห์หลายวิธีสำหรับการศึกษาประเภทนี้ วิธีการเหล่านี้อธิบายไว้ด้านล่าง วิธีการวิเคราะห์บางส่วนที่ผู้ใช้สามารถใช้ในการวิเคราะห์แบบจำลองการถดถอย ได้แก่

1. การถดถอยทวินามลบ

วิธีการถดถอยทวินามเชิงลบจะใช้เมื่อมีข้อมูลกระจายมากเกินไป ซึ่งหมายความว่าค่าของความแปรปรวนตามเงื่อนไขจะสูงกว่าหรือสูงกว่าค่าของค่าเฉลี่ยตามเงื่อนไข วิธีการนี้ถือเป็นวิธีทั่วไปจากวิธีถดถอยปัวซอง เนื่องจากทั้งสองวิธีมีโครงสร้างค่าเฉลี่ยเหมือนกัน แต่มีพารามิเตอร์เพิ่มเติมในการถดถอยทวินามเชิงลบที่ใช้ในการสร้างแบบจำลองการกระจายเกิน ช่วงความเชื่อมั่นจะถือว่าแคบกว่าการถดถอยของกิเลสเมื่อการกระจายแบบมีเงื่อนไขกระจายตัวมากเกินไปจากตัวแปรผลลัพธ์

2. การถดถอยปัวซอง

วิธีการถดถอยปัวซองใช้ในการสร้างแบบจำลองข้อมูลการนับ สามารถใช้ส่วนขยายจำนวนมากเพื่อสร้างแบบจำลองตัวแปรการนับในการถดถอยปัวซอง

3. การถดถอย OLS

ผลลัพธ์ของตัวแปรการนับจะถูกแปลงบันทึกเป็นบางครั้ง จากนั้นจึงวิเคราะห์โดยใช้วิธีการถดถอย OLS อย่างไรก็ตาม มีบางครั้งที่เกี่ยวข้องกับวิธีการถดถอย OLS ปัญหาเหล่านี้อาจทำให้ข้อมูลสูญหายเนื่องจากการสร้างค่าที่ไม่ได้กำหนดโดยการพิจารณาบันทึกของค่าศูนย์ นอกจากนี้ มันอาจจะถูกสร้างขึ้นเนื่องจากขาดการสร้างแบบจำลองข้อมูลที่กระจัดกระจาย

4. รุ่นที่ไม่มีลม

โมเดลประเภทนี้พยายามคำนวณค่าศูนย์ส่วนเกินทั้งหมดในแบบจำลอง

การวิเคราะห์โดยใช้การถดถอยทวินามเชิงลบ

คำสั่ง “nbreg” ใช้สำหรับประมาณแบบจำลองของการถดถอยทวินามเชิงลบ มีตัว "i" นำหน้าตัวแปร "prog" การมีอยู่ของ "i" บ่งชี้ว่าตัวแปรนั้นเป็นปัจจัยประเภท เช่น ตัวแปรหมวดหมู่ ควรรวมสิ่งเหล่านี้เป็นตัวแปรตัวบ่งชี้ในแบบจำลอง

• เอาต์พุตของโมเดลเริ่มต้นด้วยบันทึกการวนซ้ำ มันเริ่มต้นจากการปรับโมเดลของปัวซอง ตามด้วยโมเดล null และจากนั้นโมเดลของทวินามเชิงลบ วิธีนี้ใช้ค่าประมาณของความเป็นไปได้สูงสุดและวนซ้ำจนกว่าจะมีการเปลี่ยนแปลงค่าของบันทึกสุดท้าย ความน่าจะเป็นของบันทึกจะใช้สำหรับการเปรียบเทียบรุ่นต่างๆ
• ข้อมูลต่อไปอยู่ในไฟล์ส่วนหัว
• มีข้อมูลสัมประสิทธิ์ของการถดถอยทวินามเชิงลบอยู่ใต้ส่วนหัว ค่าสัมประสิทธิ์ถูกสร้างขึ้นสำหรับทุกตัวแปรพร้อมกับข้อผิดพลาดเช่นค่า p, z-score นอกจากนี้ยังมีช่วงความเชื่อมั่น 95% สำหรับสัมประสิทธิ์ทั้งหมด ค่าสัมประสิทธิ์สำหรับตัวแปร "คณิตศาสตร์" คือ -0.006 ซึ่งแสดงว่ามีนัยสำคัญทางสถิติ ผลลัพธ์หมายความว่าหากมีการเพิ่มขึ้นของหนึ่งหน่วยในตัวแปร "คณิตศาสตร์" จำนวนบันทึกที่คาดหวังสำหรับจำนวนวันที่ขาดหายไปจะลดลงเป็น 0.006 นอกจากนี้ ค่าของโปรก 2 ซึ่งเป็นตัวแปรตัวบ่งชี้ คือความแตกต่างที่คาดหวังในการนับบันทึกระหว่างสองกลุ่ม ( กลุ่ม 2 และกลุ่มอ้างอิง)
• การประมาณค่าพารามิเตอร์สำหรับการบันทึกที่ถ่ายโอนเกินกระจายเสร็จสิ้นแล้ว จากนั้นแสดงด้วยค่าที่ยังไม่ได้แปลง ในแบบจำลองปัวซอง ค่าเป็นศูนย์
• มีข้อมูลความน่าจะเป็นในการทดสอบอัตราส่วนด้านล่างตารางค่าสัมประสิทธิ์ โมเดลนี้สามารถเข้าใจเพิ่มเติมได้โดยใช้คำสั่ง "ระยะขอบ"

กระบวนการทำการวิเคราะห์การถดถอยทวินามเชิงลบใน Python

แพ็คเกจที่จำเป็นสำหรับการดำเนินการถดถอยจะต้องนำเข้าจาก Python แพ็คเกจเหล่านี้มีการระบุไว้ด้านล่าง:

• นำเข้า statsmodels.api เป็น sm
• นำเข้า matplotlib.pyplot เป็น plt
• นำเข้า numpy เป็น np
• จาก patsy import dmatrices
• นำเข้าแพนด้าเป็น pd

ข้อควรพิจารณาสำหรับการถดถอยทวินามเชิงลบ

มีบางสิ่งที่ควรพิจารณาในขณะที่ใช้วิธีการวิเคราะห์การถดถอยทวินามเชิงลบ ซึ่งรวมถึง:

• หากมีตัวอย่างขนาดเล็ก ไม่แนะนำให้ใช้วิธีการถดถอยทวินามเชิงลบ
• บางครั้งมีศูนย์ส่วนเกินอยู่ซึ่งอาจเป็นสาเหตุของการกระจายตัวมากเกินไป ศูนย์เหล่านี้อาจถูกสร้างขึ้นเนื่องจากกระบวนการเพิ่มการสร้างข้อมูล หากเกิดกรณีดังกล่าวขึ้น ขอแนะนำให้ใช้วิธีแบบไม่มีลม
• หากกระบวนการสร้างข้อมูลไม่นับศูนย์ใด ๆ ในกรณีนี้ ขอแนะนำให้ใช้วิธีของแบบจำลองที่ถูกตัดทอนเป็นศูนย์
• มีตัวแปรการรับแสงที่เกี่ยวข้องกับข้อมูลการนับ ตัวแปรแสดงถึงเวลาที่มีโอกาสเกิดเหตุการณ์ได้ ตัวแปรนี้จำเป็นต้องรวมเข้ากับแบบจำลองของการถดถอยทวินามเชิงลบ ทำได้โดยใช้ตัวเลือกของ exp()
• ตัวแปรผลลัพธ์ไม่สามารถเป็นค่าลบใดๆ ในแบบจำลองการวิเคราะห์การถดถอยทวินามเชิงลบ นอกจากนี้ ตัวแปรการรับแสงไม่สามารถมีค่าเป็น 0 ได้
• คำสั่ง “glm” ยังสามารถใช้สำหรับรันวิธีการวิเคราะห์การถดถอยทวินามเชิงลบ ซึ่งสามารถทำได้ผ่านลิงก์ของล็อกและแฟมิลีของทวินาม
• ต้องใช้คำสั่ง "glm" ในการรับส่วนที่เหลือ เพื่อตรวจสอบว่ามีข้อสันนิษฐานอื่นใดในรูปแบบการถดถอยทวินามเชิงลบหรือไม่
• มีการดำรงอยู่ของการวัดต่าง ๆ ของ pseudo-R-squared อย่างไรก็ตาม ทุกการวัดจะให้ข้อมูลที่คล้ายกับข้อมูลที่ได้จาก R-squared ในการถดถอยของ OLS

บทสรุป

บทความนี้กล่าวถึงหัวข้อของ การถดถอยทวินามเชิง ลบ เราได้เห็นแล้วว่าเกือบจะคล้ายกับวิธีการถดถอยพหุคูณและเป็นรูปแบบทั่วไปของการแจกแจงปัวซอง มีวิธีการใช้งานหลายวิธี เทคนิคนี้สามารถนำไปใช้ผ่านภาษาโปรแกรม python หรือในภาษา R

มีกรณีศึกษาหลายกรณีที่แสดงการประยุกต์ใช้ในการศึกษาเช่นอายุ นอกจากนี้ แบบจำลองคลาสสิกของการถดถอยที่สามารถใช้กับข้อมูลการนับได้ ได้แก่ การถดถอยปัวซอง การถดถอยทวินามเชิงลบ และการถดถอยทางเรขาคณิต วิธีการเหล่านี้เป็นของตระกูลของตัวแบบเชิงเส้นและถูกรวมอยู่ในแพ็คเกจทางสถิติเกือบทั้งหมด เช่น ระบบ R

หากคุณต้องการเก่งด้านแมชชีนเลิร์นนิงและต้องการสำรวจข้อมูล คุณสามารถตรวจสอบหลักสูตร Executive PG Program ใน Machine Learning & AI ที่นำเสนอโดย upGrad ดังนั้น หากคุณคือมืออาชีพด้านการทำงานที่ใฝ่ฝันอยากจะเป็นผู้เชี่ยวชาญด้านแมชชีนเลิร์นนิง มารับประสบการณ์การฝึกอบรมภายใต้ผู้เชี่ยวชาญ รายละเอียดเพิ่มเติมสามารถทำได้ผ่านทางเว็บไซต์ของเรา สำหรับข้อสงสัยใด ๆ ทีมงานของเราสามารถช่วยเหลือคุณได้ทันที

ยกระดับอาชีพของคุณในการเรียนรู้ของเครื่องและปัญญาประดิษฐ์

สมัครตอนนี้สำหรับ Executive Certification ใน Ai-ml จาก IIITB