เรียนรู้อัลกอริทึม Naive Bayes สำหรับการเรียนรู้ของเครื่อง [พร้อมตัวอย่าง]
เผยแพร่แล้ว: 2021-02-25สารบัญ
บทนำ
ในวิชาคณิตศาสตร์และการเขียนโปรแกรม วิธีแก้ปัญหาที่ง่ายที่สุดบางวิธีมักเป็นวิธีแก้ปัญหาที่ทรงพลังที่สุด อัลกอริธึม Bayes ไร้เดียงสามาเป็นตัวอย่างคลาสสิกของคำสั่งนี้ แม้ว่าจะมีความก้าวหน้าและการพัฒนาในด้าน Machine Learning ที่แข็งแกร่งและรวดเร็ว Algorithm ของ Naive Bayes นี้ยังคงแข็งแกร่งในฐานะอัลกอริธึมที่ใช้กันอย่างแพร่หลายและมีประสิทธิภาพมากที่สุดตัวหนึ่ง อัลกอริทึม Bayes ที่ไร้เดียงสาพบการใช้งานในปัญหาต่างๆ รวมถึงงานการจำแนกประเภทและปัญหาการประมวลผลภาษาธรรมชาติ (NLP)
สมมติฐานทางคณิตศาสตร์ของทฤษฎีบทเบย์ทำหน้าที่เป็นแนวคิดพื้นฐานที่อยู่เบื้องหลังอัลกอริทึม Naive Bayes นี้ ในบทความนี้ เราจะพูดถึงพื้นฐานของ Bayes Theorem, Naive Bayes Algorithm ควบคู่ไปกับการใช้งานใน Python พร้อมตัวอย่างปัญหาแบบเรียลไทม์ นอกจากนี้ เราจะพิจารณาข้อดีและข้อเสียของอัลกอริทึม Naive Bayes เมื่อเทียบกับคู่แข่ง
พื้นฐานของความน่าจะเป็น
ก่อนที่เราจะออกไปทำความเข้าใจเกี่ยวกับทฤษฎีบท Bayes และอัลกอริทึมของ Naive Bayes ให้เราทำความเข้าใจความรู้ที่มีอยู่ของเราเกี่ยวกับพื้นฐานของความน่าจะเป็นก่อน
ดังที่เราทุกคนทราบโดยคำจำกัดความ เมื่อพิจารณาจากเหตุการณ์ A ความน่าจะเป็นของเหตุการณ์นั้นจะเกิดขึ้นโดย P(A) ในความน่าจะเป็น สองเหตุการณ์ A และ B ถูกเรียกว่าเป็นเหตุการณ์อิสระ ถ้าการเกิดของเหตุการณ์ A ไม่เปลี่ยนแปลงความน่าจะเป็นของการเกิดเหตุการณ์ B และในทางกลับกัน ในทางกลับกัน หากเหตุการณ์หนึ่งเปลี่ยนแปลงความน่าจะเป็นของอีกเหตุการณ์หนึ่ง จะเรียกว่าเหตุการณ์ที่ขึ้นต่อกัน
เรามาทำความรู้จักกับคำศัพท์ใหม่ที่เรียกว่า Conditional Probability ในวิชาคณิตศาสตร์ ความน่าจะเป็นแบบมีเงื่อนไขสำหรับสองเหตุการณ์ A และ B ที่กำหนดโดย P (A| B) ถูกกำหนดให้เป็นความน่าจะเป็นของการเกิดเหตุการณ์ A เนื่องจากเหตุการณ์ B ได้เกิดขึ้นแล้ว ขึ้นอยู่กับความสัมพันธ์ระหว่างสองเหตุการณ์ A และ B ว่าเหตุการณ์นั้นขึ้นอยู่กับหรือเป็นอิสระ ความน่าจะเป็นแบบมีเงื่อนไขคำนวณได้สองวิธี
- ความน่าจะเป็นแบบมีเงื่อนไขของสอง เหตุการณ์ที่ขึ้น ต่อกัน A และ B ถูกกำหนดโดย P (A| B) = P (A และ B) / P (B)
- นิพจน์สำหรับความน่าจะเป็นแบบมีเงื่อนไขของสอง เหตุการณ์อิสระ A และ B ถูกกำหนดโดย P (A| B) = P (A)
เมื่อรู้คณิตศาสตร์เบื้องหลังความน่าจะเป็นและความน่าจะเป็นตามเงื่อนไขแล้ว ให้เราไปต่อกันที่ทฤษฎีบทเบย์

ทฤษฎีบทเบย์
ในสถิติและทฤษฎีความน่าจะเป็น ทฤษฎีบทของเบย์หรือที่เรียกว่ากฎของเบย์ใช้เพื่อกำหนดความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ กล่าวอีกนัยหนึ่ง ทฤษฎีบทของเบย์อธิบายความน่าจะเป็นของเหตุการณ์โดยพิจารณาจากความรู้เดิมเกี่ยวกับเงื่อนไขที่อาจเกี่ยวข้องกับเหตุการณ์
เพื่อให้เข้าใจในวิธีที่ง่ายขึ้น พิจารณาว่าเราจำเป็นต้องรู้ความน่าจะเป็นของราคาบ้านที่สูงมาก หากเราทราบเกี่ยวกับปัจจัยอื่นๆ เช่น การมีโรงเรียน ร้านขายยา และโรงพยาบาลในบริเวณใกล้เคียง เราก็จะสามารถทำการประเมินสิ่งเดียวกันได้แม่นยำยิ่งขึ้น นี่คือสิ่งที่ทฤษฎีบทเบย์ดำเนินการ
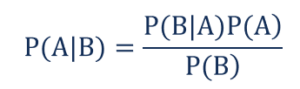
ดังนั้น,
- P(A|B) – ความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ A ที่เกิดขึ้น โดยที่เหตุการณ์ B ได้เกิดขึ้นหรือที่เรียก ว่าความน่าจะเป็น ภายหลัง
- P(B|A) – ความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ B ที่เกิดขึ้น โดยที่เหตุการณ์ A ได้เกิดขึ้นแล้ว หรือที่เรียก ว่าความน่าจะเป็น ของ โอกาส
- P(A) – ความน่าจะเป็นของเหตุการณ์ A ที่เกิดขึ้นหรือที่เรียก ว่าความน่าจะเป็นก่อนหน้า
- P(B) – ความน่าจะเป็นของเหตุการณ์ B ที่เกิดขึ้นหรือที่เรียก ว่าความน่าจะเป็นส่วนเพิ่ม
สมมติว่าเรามีปัญหาการเรียนรู้ของเครื่องอย่างง่ายกับตัวแปรอิสระ 'n' และตัวแปรตามซึ่งเป็นผลลัพธ์คือค่าบูลีน (จริงหรือเท็จ) สมมติว่าแอตทริบิวต์อิสระมีลักษณะตามหมวดหมู่ ให้เราพิจารณา 2 หมวดหมู่สำหรับตัวอย่างนี้ ดังนั้น ด้วยข้อมูลเหล่านี้ เราจำเป็นต้องคำนวณค่าของความน่าจะเป็นที่น่าจะเป็น P(B|A)
ดังนั้น จากการสังเกตข้างต้น เราพบว่าเราจำเป็นต้องคำนวณพารามิเตอร์ 2*(2^ n -1 ) เพื่อเรียนรู้โมเดลแมชชีนเลิร์นนิงนี้ ในทำนองเดียวกัน หากเรามีแอตทริบิวต์อิสระแบบบูลีน 30 รายการ จำนวนพารามิเตอร์ทั้งหมดที่จะคำนวณจะใกล้เคียงกับ 3 พันล้าน ซึ่งเป็นต้นทุนในการคำนวณที่สูงมาก
ความยากลำบากในการสร้างแบบจำลองแมชชีนเลิร์นนิงด้วยทฤษฎีบทเบย์ทำให้เกิดการกำเนิดและการพัฒนาอัลกอริธึม Naive Bayes
อัลกอริธึม Naive Bayes
เพื่อให้ใช้งานได้จริง จำเป็นต้องลดความซับซ้อนที่กล่าวถึงข้างต้นของทฤษฎีบทเบย์ นี่คือความสำเร็จอย่างแท้จริงในอัลกอริธึม Naive Bayes โดยการตั้งสมมติฐานสองสามข้อ สมมติฐานที่ตั้งขึ้นคือแต่ละคุณลักษณะมีส่วนสนับสนุนที่เป็น อิสระ และ เท่าเทียมกัน ในผลลัพธ์
อัลกอริธึม Bayes ไร้เดียงสาเป็นอัลกอริธึมการเรียนรู้ภายใต้การดูแลและอิงตามทฤษฎีบท Bayes ซึ่งใช้เป็นหลักในการแก้ปัญหาการจำแนกประเภท มันเป็นหนึ่งในตัวแยกประเภทที่ง่ายและแม่นยำที่สุดซึ่งสร้างแบบจำลองการเรียนรู้ของเครื่องเพื่อคาดการณ์อย่างรวดเร็ว ในทางคณิตศาสตร์ มันเป็นตัวแยกประเภทความน่าจะเป็น เนื่องจากมันทำการทำนายโดยใช้ฟังก์ชันความน่าจะเป็นของเหตุการณ์
ตัวอย่างปัญหา
เพื่อให้เข้าใจตรรกะเบื้องหลังสมมติฐาน ให้เราพิจารณาชุดข้อมูลง่ายๆ เพื่อให้ได้สัญชาตญาณที่ดีขึ้น
| สี | พิมพ์ | ต้นทาง | ขโมย? |
| สีดำ | เก๋ง | นำเข้า | ใช่ |
| สีดำ | SUV | นำเข้า | ไม่ |
| สีดำ | เก๋ง | ภายในประเทศ | ใช่ |
| สีดำ | เก๋ง | นำเข้า | ไม่ |
| สีน้ำตาล | SUV | ภายในประเทศ | ใช่ |
| สีน้ำตาล | SUV | ภายในประเทศ | ไม่ |
| สีน้ำตาล | เก๋ง | นำเข้า | ไม่ |
| สีน้ำตาล | SUV | นำเข้า | ใช่ |
| สีน้ำตาล | เก๋ง | ภายในประเทศ | ไม่ |
จากชุดข้อมูลที่ระบุข้างต้น เราสามารถรับแนวคิดของสมมติฐานสองข้อที่เรากำหนดไว้สำหรับอัลกอริทึม Naive Bayes ด้านบน
- ข้อสันนิษฐานแรกคือคุณลักษณะทั้งหมดเป็นอิสระจากกัน ในที่นี้ เราจะเห็นว่าแต่ละคุณลักษณะมีความเป็นอิสระ เช่น สี “สีแดง” ไม่ ขึ้น กับประเภทและที่มาของรถ
- ถัดไป แต่ละคุณลักษณะจะต้องได้รับความสำคัญเท่าเทียมกัน ในทำนองเดียวกัน การมีความรู้เกี่ยวกับประเภทและที่มาของรถเท่านั้นไม่เพียงพอที่จะทำนายผลลัพธ์ของปัญหา ดังนั้นจึงไม่มีตัวแปรใดที่ไม่เกี่ยวข้องและด้วยเหตุนี้ทั้งหมดจึงมี ส่วนสนับสนุนผลลัพธ์ที่ เท่าเทียมกัน
สรุปได้ว่า A และ B มีความเป็นอิสระตามเงื่อนไขโดยที่ C นั้นก็ต่อเมื่อ เมื่อได้รับรู้ว่า C เกิดขึ้น การรู้ว่า A เกิดขึ้นหรือไม่นั้นไม่ได้ให้ข้อมูลเกี่ยวกับความเป็นไปได้ที่ B จะเกิดขึ้น และความรู้ว่า B จะเกิดขึ้นหรือไม่นั้นไม่ได้ให้ข้อมูล ความน่าจะเป็นของการเกิด A สมมติฐานเหล่านี้ทำให้อัลกอริธึม Bayes – Naive จึงเป็นที่มาของชื่อ Naive Bayes Algorithm
ดังนั้นสำหรับปัญหาข้างต้น ทฤษฎีบทเบย์สามารถเขียนใหม่ได้เป็น –
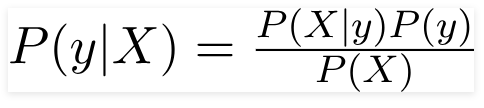
ดังนั้น,
- เวกเตอร์คุณลักษณะอิสระ X = (x 1 , x 2 , x 3 ……x n ) ที่แสดงคุณลักษณะต่างๆ เช่น สี ประเภท และที่มาของรถ
- ตัวแปรเอาต์พุต y มีเพียงสองผลลัพธ์ใช่หรือไม่ใช่
ดังนั้นโดยการแทนที่ค่าข้างต้น เราจะได้สูตร Naive Bayes เป็น
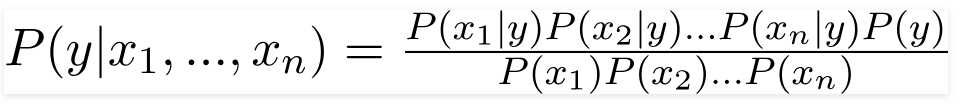
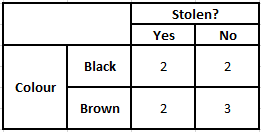
ในการคำนวณความน่าจะเป็นหลัง P(y|X) เราต้องสร้างตารางความถี่สำหรับแต่ละแอตทริบิวต์เทียบกับผลลัพธ์ จากนั้นแปลงตารางความถี่เป็นตารางความน่าจะเป็น หลังจากนั้นในที่สุดเราใช้สมการแบบเบส์ไร้เดียงสาเพื่อคำนวณความน่าจะเป็นหลังสำหรับแต่ละชั้นเรียน ชั้นเรียนที่มีความน่าจะเป็นหลังสูงสุดจะถูกเลือกเป็นผลของการทำนาย ด้านล่างนี้คือตารางความถี่และความน่าจะเป็นสำหรับตัวทำนายทั้งสาม
ตารางความถี่ของสี ตารางความน่าจะเป็นของสี
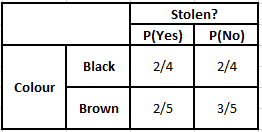
ตารางความถี่ของประเภท ความน่าจะเป็น ตารางประเภท

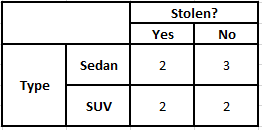
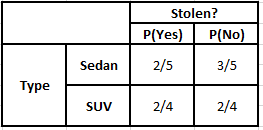
ตารางความถี่ของแหล่งกำเนิด ตารางความเป็นไปได้ของแหล่งกำเนิด
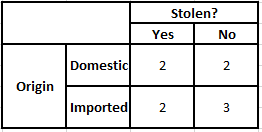
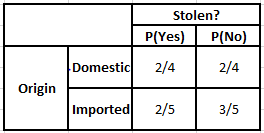
พิจารณากรณีที่เราต้องคำนวณความน่าจะเป็นหลังสำหรับเงื่อนไขด้านล่าง -
| สี | พิมพ์ | ต้นทาง |
| สีน้ำตาล | SUV | นำเข้า |
ดังนั้น จากสูตรที่กำหนดข้างต้น เราสามารถคำนวณความน่าจะเป็นด้านหลังได้ดังแสดงด้านล่าง-
P(ใช่ | X) = P(สีน้ำตาล | ใช่) * P(SUV | ใช่) * P(นำเข้า | ใช่) * P(ใช่)
= 2/5 * 2/4 * 2/5 * 1
= 0.08
P(No | X) = P(สีน้ำตาล | No) * P(SUV | No) * P(นำเข้า | No) * P(No)
= 3/5 * 2/4 * 3/5 * 1
= 0.18
จากค่าที่คำนวณข้างต้น เนื่องจากความน่าจะเป็นภายหลังสำหรับ No มีค่ามากกว่าใช่ (0.18>0.08) จึงสามารถอนุมานได้ว่ารถยนต์ที่มีสีน้ำตาล ประเภท SUV ของแหล่งกำเนิดนำเข้าถูกจัดประเภทเป็น “ไม่” ดังนั้นรถจะไม่ถูกขโมย
การใช้งานใน Python
ตอนนี้เราเข้าใจคณิตศาสตร์เบื้องหลังอัลกอริธึม Naive Bayes แล้วและได้เห็นภาพด้วยตัวอย่างแล้ว ให้เรามาดูโค้ดการเรียนรู้ของเครื่องในภาษา Python กัน
ที่เกี่ยวข้อง: ลักษณนามไร้เดียงสา
การวิเคราะห์ปัญหา
ในการใช้โปรแกรม Naive Bayes Classification ใน Machine Learning โดยใช้ Python เราจะใช้ 'Iris Flower Dataset' ที่มีชื่อเสียงมาก ชุดข้อมูลดอกไอริสหรือชุดข้อมูลไอริสของฟิชเชอร์เป็นชุดข้อมูลหลายตัวแปรที่นำเสนอโดยโรนัลด์ ฟิชเชอร์ นักสถิติ นักสุพันธุศาสตร์ และนักชีววิทยาชาวอังกฤษในปี 2541 ชุดข้อมูลนี้เป็นชุดข้อมูลพื้นฐานขนาดเล็กมากที่ประกอบด้วยข้อมูลตัวเลขน้อยมากที่มีข้อมูลเกี่ยวกับ 3 คลาส ของดอกไม้ในตระกูลไอริส ได้แก่ –
- ไอริส เซโตซ่า
- ไอริส หลากสี
- Iris Virginica
มี 50 ตัวอย่างของแต่ละชนิดใน สามสปีชี ส์ ซึ่งรวมเป็นชุดข้อมูลทั้งหมด 150 แถว 4 คุณลักษณะ (หรือ) ตัวแปรอิสระที่ใช้ในชุดข้อมูลนี้คือ –
- ความยาวของกลีบเลี้ยงในหน่วย cm
- ความกว้างของกลีบเลี้ยงเป็นซม.
- ความยาวกลีบเป็นซม.
- ความกว้างของกลีบเป็นซม.
ตัวแปรตามคือ "สปี ชี ส์" ของดอกไม้ที่ระบุโดยคุณลักษณะสี่ประการที่ระบุข้างต้น
ขั้นตอนที่ 1 – การนำเข้าไลบรารี
และเช่นเคย ขั้นตอนหลักในการสร้างแบบจำลองแมชชีนเลิร์นนิงคือการนำเข้าไลบรารีที่เกี่ยวข้อง สำหรับสิ่งนี้ เราจะโหลดไลบรารี NumPy, Mathplotlib และ Pandas เพื่อประมวลผลข้อมูลล่วงหน้า
นำเข้า numpy เป็น np
นำเข้า matplotlib.pyplot เป็น plt
นำเข้าแพนด้าเป็น pd
ขั้นตอนที่ 2 – กำลังโหลดชุดข้อมูล
ชุดข้อมูลดอกไอริสที่จะใช้สำหรับการฝึกตัวจำแนก Naive Bayes จะถูกโหลดลงใน Pandas DataFrame ตัวแปรอิสระ 4 ตัวจะต้องถูกกำหนดให้กับตัวแปร X และตัวแปรของสปีชีส์เอาต์พุตสุดท้ายถูกกำหนดให้กับ y
ชุดข้อมูล = pd.read_csv (' https://raw.githubusercontent.com/mk-gurucharan/Classification/master/IrisDataset.csv' )X = dataset.iloc[:,:4].values
y = ชุดข้อมูล['species'].valuesdataset.head(5)>>
sepal_length sepal_width petal_length petal_width สายพันธุ์
5.1 3.5 1.4 0.2 เซโตซ่า
4.9 3.0 1.4 0.2 เซโตซา
4.7 3.2 1.3 0.2 เซโตซา
4.6 3.1 1.5 0.2 เซโตซา
5.0 3.6 1.4 0.2 เซโตซา
ขั้นตอนที่ 3 – แยกชุดข้อมูลออกเป็นชุดการฝึกและชุดทดสอบ
หลังจากโหลดชุดข้อมูลและตัวแปรแล้ว ขั้นตอนต่อไปคือการเตรียมตัวแปรที่จะผ่านกระบวนการฝึกอบรม ในขั้นตอนนี้ เราต้องแยกตัวแปร X และ y ออกเป็นการฝึกและชุดข้อมูลการทดสอบ สำหรับสิ่งนี้ เราจะกำหนด 80% ของข้อมูลแบบสุ่มให้กับชุดการฝึก ซึ่งจะใช้เพื่อวัตถุประสงค์ในการฝึกอบรม และอีก 20% ที่เหลือของข้อมูลเป็นชุดการทดสอบที่ Naive Bayes Classifier ที่ผ่านการฝึกอบรมจะได้รับการทดสอบเพื่อความถูกต้อง
จาก sklearn.model_selection นำเข้า train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
ขั้นตอนที่ 4 – การปรับขนาดคุณสมบัติ
แม้ว่านี่จะเป็นกระบวนการเพิ่มเติมสำหรับชุดข้อมูลขนาดเล็กนี้ แต่ฉันกำลังเพิ่มสิ่งนี้ให้คุณเพื่อใช้ในชุดข้อมูลขนาดใหญ่ขึ้น ในการนี้ ข้อมูลในชุดการฝึกและการทดสอบจะถูกลดขนาดลงเป็นช่วงของค่าระหว่าง 0 ถึง 1 ซึ่งจะช่วยลดต้นทุนในการคำนวณ
จาก sklearn.preprocessing นำเข้า StandardScaler
sc = StandardScaler ()
X_train = sc.fit_transform (X_train)
X_test = sc.transform (X_test)
ขั้นตอนที่ 5 – ฝึกโมเดลการจำแนก Naive Bayes บนชุดการฝึก
อยู่ในขั้นตอนนี้ที่เรานำเข้าคลาส Naive Bayes จากไลบรารี sklearn สำหรับรุ่นนี้ เราใช้โมเดล Gaussian มีอีกหลายรุ่น เช่น Bernoulli, Categorical และ Multinomial ดังนั้น X_train และ y_train จึงพอดีกับตัวแปรลักษณนามเพื่อวัตถุประสงค์ในการฝึกอบรม
จาก sklearn.naive_bayes นำเข้า GaussianNB
ลักษณนาม = GaussianNB()
classifier.fit(X_train, y_train)
ขั้นตอนที่ 6 – การทำนายผลชุดทดสอบ –
เราทำนายคลาสของสปีชีส์สำหรับชุดการทดสอบโดยใช้แบบจำลองที่ฝึกและเปรียบเทียบกับค่าจริงของคลาสสปีชีส์
y_pred = classifier.predict(X_test)
df = pd.DataFrame({'ค่าจริง':y_test, 'ค่าที่คาดการณ์':y_pred})
df>>
มูลค่าที่แท้จริง ค่าที่คาดการณ์
เซโตซ่า เซโตซ่า
เซโตซ่า เซโตซ่า
virginica เวอร์จิน
versicolor versicolor
เซโตซ่า เซโตซ่า
เซโตซ่า เซโตซ่า
… … … … …
virginica versicolor
virginica เวอร์จิน
เซโตซ่า เซโตซ่า
เซโตซ่า เซโตซ่า
versicolor versicolor
versicolor versicolor
ในการเปรียบเทียบข้างต้น เราพบว่ามีคำทำนายที่ไม่ถูกต้องหนึ่งคำที่ทำนาย Versicolor แทน Virginica
ขั้นตอนที่ 7 – เมทริกซ์ความสับสนและความแม่นยำ
ในขณะที่เรากำลังจัดการกับการจำแนกประเภท วิธีที่ดีที่สุดในการประเมินแบบจำลองตัวแยกประเภทของเราคือการพิมพ์ Confusion Matrix พร้อมกับความแม่นยำในชุดทดสอบ
จาก sklearn.metrics นำเข้าสับสน_matrix
cm = ความสับสน_matrix(y_test, y_pred) จาก sklearn.metrics ความแม่นยำในการนำเข้า

พิมพ์ (“ความแม่นยำ : “, ความแม่นยำ_score(y_test, y_pred))
ซม.>>ความแม่นยำ : 0.96666666666666667
>>array([[14, 0, 0],
[ 0, 7, 0],
[ 0, 1, 8]])
บทสรุป
ดังนั้น ในบทความนี้ เราได้อ่านพื้นฐานของ Naive Bayes Algorithm ที่เข้าใจคณิตศาสตร์ที่อยู่เบื้องหลังการจำแนกประเภทพร้อมกับตัวอย่างที่แก้ปัญหาด้วยมือ สุดท้าย เราใช้โค้ด Machine Learning เพื่อแก้ปัญหาชุดข้อมูลยอดนิยมโดยใช้อัลกอริทึมการจำแนก Naive Bayes
หากคุณสนใจที่จะเรียนรู้เพิ่มเติมเกี่ยวกับ AI, แมชชีนเลิร์นนิง โปรดดูที่ IIIT-B & upGrad's PG Diploma in Machine Learning & AI ซึ่งออกแบบมาสำหรับมืออาชีพที่ทำงานและมีการฝึกอบรมที่เข้มงวดมากกว่า 450 ชั่วโมง กรณีศึกษาและการมอบหมายมากกว่า 30 รายการ สถานะศิษย์เก่า IIIT-B โครงการหลัก 5 โครงการและความช่วยเหลือด้านงานกับบริษัทชั้นนำ
ความน่าจะเป็นมีประโยชน์ในการเรียนรู้ของเครื่องอย่างไร
เราอาจต้องตัดสินใจโดยอิงจากข้อมูลบางส่วนหรือไม่สมบูรณ์ในสถานการณ์จริง ความน่าจะเป็นช่วยให้เราสามารถระบุความไม่แน่นอนในระบบดังกล่าวและจัดการความเสี่ยงสำหรับงาน วิธีการแบบเดิมใช้ได้ผลเฉพาะกับผลลัพธ์ที่กำหนดขึ้นสำหรับการดำเนินการเฉพาะ แต่มีขอบเขตของความไม่แน่นอนในแบบจำลองการทำนายเสมอ ความไม่แน่นอนนี้อาจมาจากพารามิเตอร์หลายอย่างจากข้อมูลที่ป้อนเข้า เช่น สัญญาณรบกวนในข้อมูล นอกจากนี้ มุมมองแบบเบย์จากทฤษฎีบทความน่าจะเป็นสามารถช่วยในการจดจำรูปแบบจากข้อมูลที่ป้อนเข้า สำหรับสิ่งนี้ ความน่าจะเป็นใช้แนวคิดการประมาณค่าความน่าจะเป็นสูงสุด และด้วยเหตุนี้จึงเป็นประโยชน์ในการสร้างผลลัพธ์ที่เกี่ยวข้อง
การใช้ Confusion Matrix คืออะไร?
เมทริกซ์ความสับสนคือเมทริกซ์ขนาด 2x2 ที่ใช้ในการตีความประสิทธิภาพของแบบจำลองการจัดหมวดหมู่ ค่าจริงสำหรับข้อมูลที่ป้อนต้องเป็นที่รู้จักจึงจะใช้งานได้ ดังนั้นจึงไม่สามารถแสดงข้อมูลที่ไม่มีป้ายกำกับได้ ประกอบด้วยจำนวนของผลบวกลวง (FP) ผลบวกจริง (TP) ผลลบลวง (FN) และผลลบจริง (TN) การคาดคะเนแบ่งออกเป็นชั้นเรียนเหล่านี้โดยใช้การนับจากชุดการฝึกและชุดทดสอบ ช่วยให้เราเห็นภาพพารามิเตอร์ที่เป็นประโยชน์ เช่น ความแม่นยำ ความแม่นยำ การเรียกคืน และความจำเพาะ มันค่อนข้างเข้าใจง่ายและให้แนวคิดที่ชัดเจนเกี่ยวกับอัลกอริทึมแก่คุณ
โมเดล Naive Bayes ประเภทต่าง ๆ มีอะไรบ้าง?
ทุกประเภทขึ้นอยู่กับทฤษฎีบทเบย์เป็นหลัก โมเดล Naive Bayes โดยทั่วไปมีสามประเภท: Gaussian, Bernoulli และ Multinomial Gaussian Naive Bayes ช่วยด้วยค่าต่อเนื่องจากพารามิเตอร์อินพุต และมีการสันนิษฐานว่าคลาสของข้อมูลอินพุตทั้งหมดมีการกระจายอย่างสม่ำเสมอ naive Bayes ของ Bernoulli เป็นโมเดลตามเหตุการณ์ โดยที่ฟีเจอร์ข้อมูลเป็นอิสระและมีอยู่ในค่าบูลีน Multinomial Naive Bayes ยังอิงตามแบบจำลองตามเหตุการณ์ มีคุณลักษณะข้อมูลในรูปแบบเวกเตอร์ ซึ่งแสดงถึงความถี่ที่เกี่ยวข้องตามเหตุการณ์ที่เกิดขึ้น
