25 คำถามและคำตอบสำหรับการสัมภาษณ์การเรียนรู้ของเครื่อง – การถดถอยเชิงเส้น
เผยแพร่แล้ว: 2022-09-08เป็นแนวทางปฏิบัติทั่วไปในการทดสอบผู้สนใจวิทยาศาสตร์ข้อมูลเกี่ยวกับอัลกอริธึมการเรียนรู้ของเครื่องที่ใช้กันทั่วไปในการสัมภาษณ์ อัลกอริธึมทั่วไปเหล่านี้ ได้แก่ การถดถอยเชิงเส้น การถดถอยโลจิสติก การจัดกลุ่ม ต้นไม้การตัดสินใจ ฯลฯ นักวิทยาศาสตร์ด้านข้อมูลคาดว่าจะมีความรู้เชิงลึกเกี่ยวกับอัลกอริธึมเหล่านี้
เราได้ปรึกษากับผู้จัดการการจ้างงานและนักวิทยาศาสตร์ข้อมูลจากองค์กรต่างๆ เพื่อทราบเกี่ยวกับคำถาม ML ทั่วไปที่พวกเขาถามในการสัมภาษณ์ จากผลตอบรับที่กว้างขวางของพวกเขา ชุดของคำถามและคำตอบถูกเตรียมไว้เพื่อช่วยนักวิทยาศาสตร์ข้อมูลที่ต้องการในการสนทนาของพวกเขา คำถามสัมภาษณ์ เชิงเส้นถดถอย เป็นคำถาม ที่พบบ่อยที่สุดในการสัมภาษณ์แมชชีนเลิร์นนิง ถาม&ตอบเกี่ยวกับอัลกอริธึมเหล่านี้จะมีอยู่ในบล็อกโพสต์สี่ชุด
สุดยอดหลักสูตรการเรียนรู้ของเครื่องและหลักสูตร AI ออนไลน์
| วิทยาศาสตรมหาบัณฑิตสาขาวิชา Machine Learning & AI จาก LJMU | Executive Post Graduate Program in Machine Learning & AI จาก IIITB | |
| โปรแกรมประกาศนียบัตรขั้นสูงในการเรียนรู้ของเครื่อง & NLP จาก IIITB | โปรแกรมประกาศนียบัตรขั้นสูงในการเรียนรู้ของเครื่องและการเรียนรู้เชิงลึกจาก IIITB | Executive Post Graduate Program in Data Science & Machine Learning จาก University of Maryland |
| หากต้องการสำรวจหลักสูตรทั้งหมดของเรา โปรดไปที่หน้าด้านล่าง | ||
| หลักสูตรการเรียนรู้ของเครื่อง | ||
โพสต์บล็อกแต่ละรายการจะครอบคลุมหัวข้อต่อไปนี้:-
- การถดถอยเชิงเส้น
- การถดถอยโลจิสติก
- การจัดกลุ่ม
- ต้นไม้การตัดสินใจและคำถามที่เกี่ยวข้องกับอัลกอริธึมทั้งหมด
มาเริ่มด้วยการถดถอยเชิงเส้นกัน!
1. การถดถอยเชิงเส้นคืออะไร?
กล่าวอย่างง่าย ๆ การถดถอยเชิงเส้นเป็นวิธีการหาความพอดีของเส้นตรงที่ดีที่สุดกับข้อมูลที่กำหนด กล่าวคือ การหาความสัมพันธ์เชิงเส้นตรงที่ดีที่สุดระหว่างตัวแปรอิสระและตัวแปรตาม
ในแง่เทคนิค การถดถอยเชิงเส้นคืออัลกอริธึมการเรียนรู้ของเครื่องที่ค้นหาความสัมพันธ์แบบเส้นตรงที่ดีที่สุดบนข้อมูลใดๆ ที่กำหนด ระหว่างตัวแปรอิสระและตัวแปรตาม ส่วนใหญ่จะทำโดยวิธีผลรวมของเศษที่เหลือ
ทักษะการเรียนรู้ของเครื่องตามความต้องการ
| หลักสูตรปัญญาประดิษฐ์ | หลักสูตร Tableau |
| หลักสูตร NLP | หลักสูตรการเรียนรู้เชิงลึก |

2. ระบุสมมติฐานในรูปแบบการถดถอยเชิงเส้น
มีสมมติฐานหลักสามข้อในแบบจำลองการถดถอยเชิงเส้น:
- สมมติฐานเกี่ยวกับรูปแบบของแบบจำลอง:
สันนิษฐานว่ามีความสัมพันธ์เชิงเส้นตรงระหว่างตัวแปรตามและตัวแปรอิสระ เรียกว่า 'สมมติฐานเชิงเส้น' - สมมติฐานเกี่ยวกับส่วนที่เหลือ:
- สมมติฐานปกติ: สันนิษฐานว่าเงื่อนไขข้อผิดพลาด ε (i) มีการแจกจ่ายตามปกติ
- สมมติฐานค่าเฉลี่ยเป็นศูนย์: สันนิษฐานว่าส่วนที่เหลือมีค่าเฉลี่ยเป็นศูนย์
- สมมติฐานความแปรปรวนคงที่: สันนิษฐานว่าเงื่อนไขที่เหลือมีความแปรปรวนเหมือนกัน (แต่ไม่ทราบ) σ 2 สมมติฐานนี้เรียกอีกอย่างว่าสมมติฐานของความเป็นเนื้อเดียวกันหรือความคล้ายคลึงกัน
- สมมติฐานข้อผิดพลาดอิสระ: สันนิษฐานว่าเงื่อนไขที่เหลือเป็นอิสระจากกัน กล่าวคือ ความแปรปรวนร่วมแบบคู่ของพวกมันเป็นศูนย์
- สมมติฐานเกี่ยวกับตัวประมาณ:
- ตัวแปรอิสระจะถูกวัดโดยไม่มีข้อผิดพลาด
- ตัวแปรอิสระมีความเป็นอิสระเชิงเส้นต่อกัน กล่าวคือ ไม่มีข้อมูลหลายเส้นตรงในข้อมูล
คำอธิบาย:
- นี่เป็นคำอธิบายในตัวเอง
- หากเศษที่เหลือไม่ได้รับการกระจายตามปกติ การสุ่มของพวกมันจะหายไป ซึ่งหมายความว่าแบบจำลองไม่สามารถอธิบายความสัมพันธ์ในข้อมูลได้
นอกจากนี้ ค่าเฉลี่ยของค่าคงเหลือควรเป็นศูนย์
Y (i)i = β 0 + β 1 x (i) + ε (i)
นี่คือแบบจำลองเชิงเส้นสมมติ โดยที่ ε คือเทอมที่เหลือ
E(Y) = E( β 0 + β 1 x (i) + ε (i) )
= E( β 0 + β 1 x (i) + ε (i) )
หากค่าความคาดหมาย (ค่าเฉลี่ย) ของค่าคงเหลือ E(ε (i) ) เป็นศูนย์ ค่าความคาดหมายของตัวแปรเป้าหมายและแบบจำลองจะเหมือนกัน ซึ่งเป็นหนึ่งในเป้าหมายของแบบจำลอง
ส่วนที่เหลือ (หรือที่เรียกว่าเงื่อนไขข้อผิดพลาด) ควรเป็นอิสระ ซึ่งหมายความว่าไม่มีความสัมพันธ์กันระหว่างค่าคงเหลือกับค่าที่คาดการณ์ไว้ หรือระหว่างค่าคงเหลือเอง หากมีความสัมพันธ์บางอย่าง แสดงว่ามีความสัมพันธ์บางอย่างที่แบบจำลองการถดถอยไม่สามารถระบุได้ - ถ้าตัวแปรอิสระไม่เป็นอิสระเชิงเส้นต่อกัน ความเป็นเอกลักษณ์ของคำตอบกำลังสองน้อยที่สุด (หรือคำตอบของสมการปกติ) จะหายไป
เข้าร่วมหลักสูตรปัญญาประดิษฐ์ออนไลน์จากมหาวิทยาลัยชั้นนำของโลก – ปริญญาโท โปรแกรม Executive Post Graduate และหลักสูตรประกาศนียบัตรขั้นสูงใน ML & AI เพื่อติดตามอาชีพของคุณอย่างรวดเร็ว
3. วิศวกรรมคุณลักษณะคืออะไร? คุณนำไปใช้ในกระบวนการสร้างแบบจำลองได้อย่างไร?
วิศวกรรมคุณลักษณะเป็นกระบวนการในการแปลงข้อมูลดิบเป็นคุณลักษณะที่แสดงถึงปัญหาพื้นฐานของแบบจำลองการคาดการณ์ได้ดีขึ้น
ส่งผลให้ความแม่นยำของแบบจำลองดีขึ้นในข้อมูลที่มองไม่เห็น
ในแง่คนธรรมดา วิศวกรรมคุณลักษณะหมายถึงการพัฒนาคุณลักษณะใหม่ที่อาจช่วยให้คุณเข้าใจและจำลองปัญหาในทางที่ดีขึ้น วิศวกรรมคุณลักษณะมีสองประเภท — ขับเคลื่อนธุรกิจและขับเคลื่อนด้วยข้อมูล วิศวกรรมคุณลักษณะที่ขับเคลื่อนด้วยธุรกิจเกี่ยวข้องกับการรวมคุณลักษณะจากมุมมองทางธุรกิจ งานที่นี่คือการแปลงตัวแปรทางธุรกิจเป็นคุณสมบัติของปัญหา ในกรณีของวิศวกรรมคุณลักษณะที่ขับเคลื่อนด้วยข้อมูล คุณลักษณะที่คุณเพิ่มไม่มีการตีความทางกายภาพที่สำคัญ แต่ช่วยแบบจำลองในการทำนายตัวแปรเป้าหมาย
FYI: หลักสูตร nlp ฟรี!
หากต้องการใช้วิศวกรรมคุณลักษณะ คุณต้องทำความคุ้นเคยกับชุดข้อมูลอย่างเต็มที่ สิ่งนี้เกี่ยวข้องกับการรู้ว่าข้อมูลที่ระบุคืออะไร หมายความว่าอย่างไร คุณสมบัติดิบคืออะไร ฯลฯ คุณต้องมีแนวคิดที่ชัดเจนเกี่ยวกับปัญหาด้วย เช่น ปัจจัยใดที่ส่งผลต่อตัวแปรเป้าหมาย การตีความทางกายภาพของตัวแปรคืออะไร ฯลฯ
4. การทำให้เป็นมาตรฐานคืออะไร? อธิบายการทำให้เป็นมาตรฐานของ L1 และ L2
การทำให้เป็นมาตรฐานเป็นเทคนิคที่ใช้ในการจัดการกับปัญหาการปรับโมเดลมากเกินไป เมื่อมีการใช้แบบจำลองที่ซับซ้อนมากกับข้อมูลการฝึกอบรม ในบางครั้ง โมเดลธรรมดาอาจไม่สามารถสรุปข้อมูลได้ และโมเดลที่ซับซ้อนเกินพอดี เพื่อแก้ไขปัญหานี้ จะใช้การทำให้เป็นมาตรฐาน
การทำให้เป็นมาตรฐานไม่มีอะไรเลยนอกจากการเพิ่มเงื่อนไขสัมประสิทธิ์ (เบต้า) ให้กับฟังก์ชันต้นทุนเพื่อให้เงื่อนไขนั้นถูกลงโทษและมีขนาดเล็ก โดยพื้นฐานแล้วจะช่วยในการจับแนวโน้มในข้อมูล และในขณะเดียวกันก็ป้องกันการ overfitting โดยไม่ปล่อยให้แบบจำลองซับซ้อนเกินไป
- การทำให้เป็นมาตรฐาน L1 หรือ LASSO: ที่นี่ ค่าสัมบูรณ์ของสัมประสิทธิ์จะถูกเพิ่มลงในฟังก์ชันต้นทุน ดังจะเห็นได้จากสมการต่อไปนี้ ส่วนที่ไฮไลต์สอดคล้องกับการปรับมาตรฐาน L1 หรือ LASSO เทคนิคการทำให้เป็นมาตรฐานนี้ให้ผลลัพธ์ที่เบาบาง ซึ่งนำไปสู่การเลือกคุณลักษณะเช่นกัน
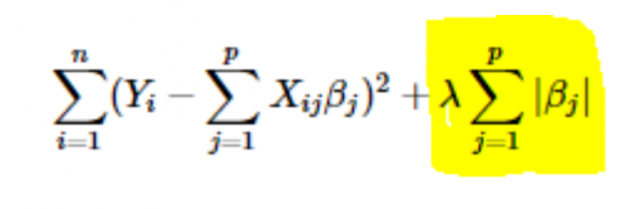
- การทำให้เป็นมาตรฐาน L2 หรือ Ridge: ในที่นี้ กำลังสองของสัมประสิทธิ์จะถูกเพิ่มลงในฟังก์ชันต้นทุน ซึ่งสามารถเห็นได้ในสมการต่อไปนี้ โดยส่วนที่ไฮไลต์สอดคล้องกับ L2 หรือการปรับแนวสันเขา
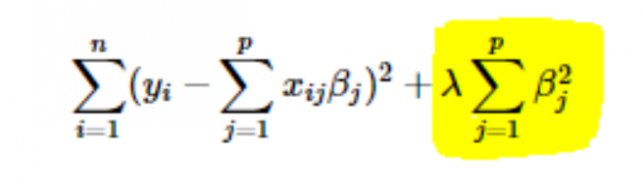
5. วิธีการเลือกค่าของอัตราการเรียนรู้พารามิเตอร์ (α)?
การเลือกมูลค่าของอัตราการเรียนรู้เป็นธุรกิจที่ยุ่งยาก หากค่าน้อยเกินไป อัลกอริธึมการไล่ระดับสีแบบเกรเดียนท์จะใช้เวลานานในการมาบรรจบกันเป็นโซลูชันที่เหมาะสมที่สุด ในทางกลับกัน หากค่าของอัตราการเรียนรู้สูง การไล่ระดับการไล่ระดับจะเกินวิธีแก้ปัญหาที่เหมาะสมที่สุด และไม่น่าจะมาบรรจบกันกับโซลูชันที่เหมาะสมที่สุด
เพื่อแก้ปัญหานี้ คุณสามารถลองใช้ค่าอัลฟ่าที่แตกต่างกันในช่วงของค่าต่างๆ และพล็อตต้นทุนเทียบกับจำนวนการวนซ้ำ จากนั้น สามารถเลือกค่าที่สอดคล้องกับกราฟที่แสดงการลดลงอย่างรวดเร็วตามกราฟได้ 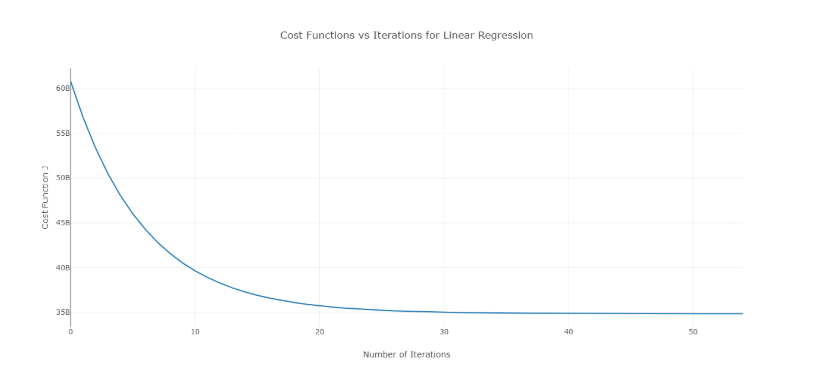
กราฟดังกล่าวเป็นต้นทุนในอุดมคติเทียบกับจำนวนเส้นโค้งการวนซ้ำ โปรดทราบว่าต้นทุนในขั้นต้นจะลดลงเมื่อจำนวนการวนซ้ำเพิ่มขึ้น แต่หลังจากการทำซ้ำบางอย่าง การไล่ระดับการไล่ระดับจะบรรจบกันและต้นทุนจะไม่ลดลงอีกต่อไป
หากคุณเห็นว่าค่าใช้จ่ายเพิ่มขึ้นตามจำนวนการทำซ้ำ แสดงว่าพารามิเตอร์อัตราการเรียนรู้ของคุณสูงและจำเป็นต้องลดลง
6. จะเลือกค่าของพารามิเตอร์การทำให้เป็นมาตรฐาน (λ) ได้อย่างไร?
การเลือกพารามิเตอร์การทำให้เป็นมาตรฐานเป็นเรื่องยุ่งยาก หากค่าของ λ สูงเกินไป จะนำไปสู่ค่าสัมประสิทธิ์การถดถอยที่น้อยมาก β ซึ่ง จะนำไปสู่แบบจำลองที่ไม่เหมาะสม (ความเอนเอียงสูง - ความแปรปรวนต่ำ) ในทางกลับกัน หากค่าของ λ เป็น 0 (น้อยมาก) ตัวแบบจะมีแนวโน้มมากเกินไปกับข้อมูลการฝึก (ความเอนเอียงต่ำ – ความแปรปรวนสูง)
ไม่มีวิธีที่เหมาะสมในการเลือกค่าของ λ สิ่งที่คุณสามารถทำได้คือมีตัวอย่างข้อมูลย่อยและเรียกใช้อัลกอริทึมหลายครั้งในชุดต่างๆ ที่นี่บุคคลต้องตัดสินใจว่าจะทนต่อความแปรปรวนได้มากน้อยเพียงใด เมื่อผู้ใช้พอใจกับความแปรปรวนแล้ว ค่าของ λ นั้นสามารถเลือกเป็นชุดข้อมูลทั้งหมดได้
สิ่งหนึ่งที่ควรสังเกตคือค่าของ λ ที่เลือกที่นี่เหมาะสมที่สุดสำหรับเซตย่อยนั้น ไม่ใช่สำหรับข้อมูลการฝึกทั้งหมด
7. เราสามารถใช้การถดถอยเชิงเส้นสำหรับการวิเคราะห์อนุกรมเวลาได้หรือไม่?
สามารถใช้การถดถอยเชิงเส้นสำหรับการวิเคราะห์อนุกรมเวลาได้ แต่ผลลัพธ์ไม่น่าเป็นไปได้ ดังนั้นจึงไม่แนะนำให้ทำเช่นนั้นโดยทั่วไป เหตุผลเบื้องหลังนี้คือ—
- ข้อมูลอนุกรมเวลาส่วนใหญ่ใช้สำหรับการทำนายอนาคต แต่การถดถอยเชิงเส้นไม่ค่อยให้ผลลัพธ์ที่ดีสำหรับการคาดการณ์ในอนาคต เนื่องจากไม่ได้มีไว้สำหรับการอนุมาน
- โดยส่วนใหญ่ ข้อมูลอนุกรมเวลามีรูปแบบ เช่น ในช่วงเวลาที่มีผู้ใช้บริการสูงสุด ช่วงเทศกาล ฯลฯ ซึ่งมักจะถือว่าเป็นค่าผิดปกติในการวิเคราะห์การถดถอยเชิงเส้น
8. ผลรวมของเศษเหลือของการถดถอยเชิงเส้นมีค่าเท่ากับเท่าใด ให้เหตุผล
Ans ผลรวมของเศษเหลือของการถดถอยเชิงเส้นคือ 0 การถดถอยเชิงเส้นทำงานบนสมมติฐานที่ว่าข้อผิดพลาด (ส่วนที่เหลือ) ปกติจะกระจายด้วยค่าเฉลี่ย 0 คือ
Y = β T X + ε
โดยที่ Y คือเป้าหมายหรือตัวแปรตาม
β คือเวกเตอร์ของสัมประสิทธิ์การถดถอย
X คือเมทริกซ์คุณลักษณะที่มีคุณลักษณะทั้งหมดเป็นคอลัมน์
ε เป็นเทอมที่เหลือซึ่ง ε ~ N(0,σ 2 )
ดังนั้น ผลรวมของเศษที่เหลือทั้งหมดจึงเป็นมูลค่าที่คาดไว้ของเศษเหลือคูณจำนวนจุดข้อมูลทั้งหมด เนื่องจากความคาดหวังของส่วนที่เหลือเป็น 0 ผลรวมของเทอมที่เหลือทั้งหมดจึงเป็นศูนย์
หมายเหตุ : N(μ,σ 2 ) เป็นสัญกรณ์มาตรฐานสำหรับการแจกแจงแบบปกติที่มีค่าเฉลี่ย μ และค่าเบี่ยงเบนมาตรฐาน σ 2
9. multicollinearity ส่งผลต่อการถดถอยเชิงเส้นอย่างไร
Ans Multicollinearity เกิดขึ้นเมื่อตัวแปรอิสระบางตัวมีความสัมพันธ์สูง (บวกหรือลบ) ซึ่งกันและกัน พหุเส้นตรงนี้ทำให้เกิดปัญหาเนื่องจากขัดกับสมมติฐานพื้นฐานของการถดถอยเชิงเส้น การปรากฏตัวของ multicollinearity ไม่ส่งผลต่อความสามารถในการคาดการณ์ของแบบจำลอง ดังนั้น หากคุณต้องการแค่การคาดคะเน การมีอยู่ของหลายคอลลิเนียร์ก็ไม่ส่งผลต่อผลลัพธ์ของคุณ อย่างไรก็ตาม หากคุณต้องการดึงข้อมูลเชิงลึกจากแบบจำลองและนำไปใช้ สมมติว่ารูปแบบธุรกิจบางอย่างอาจทำให้เกิดปัญหาได้
ปัญหาสำคัญประการหนึ่งที่เกิดจากความหลากหลายร่วมคือมันนำไปสู่การตีความที่ไม่ถูกต้องและให้ข้อมูลเชิงลึกที่ไม่ถูกต้อง ค่าสัมประสิทธิ์ของการถดถอยเชิงเส้นแนะนำการเปลี่ยนแปลงเฉลี่ยในค่าเป้าหมายหากจุดสนใจถูกเปลี่ยนโดยหนึ่งหน่วย ดังนั้น หาก multicollinearity มีอยู่ สิ่งนี้ไม่ถือเป็นจริงเนื่องจากการเปลี่ยนแปลงคุณลักษณะหนึ่งจะนำไปสู่การเปลี่ยนแปลงในตัวแปรที่สัมพันธ์กันและการเปลี่ยนแปลงที่ตามมาในตัวแปรเป้าหมาย สิ่งนี้นำไปสู่ข้อมูลเชิงลึกที่ผิดพลาดและสามารถสร้างผลลัพธ์ที่เป็นอันตรายสำหรับธุรกิจได้
วิธีที่มีประสิทธิภาพสูงในการจัดการกับความหลากหลายทางชีวภาพคือการใช้ VIF (Variance Inflation Factor) ค่าของ VIF สำหรับจุดสนใจสูงขึ้น ความสัมพันธ์เชิงเส้นตรงมากขึ้นคือจุดสนใจนั้น เพียงลบคุณสมบัติที่มีค่า VIF สูงมาก และฝึกโมเดลอีกครั้งบนชุดข้อมูลที่เหลือ
10. รูปแบบปกติ (สมการ) ของการถดถอยเชิงเส้นคืออะไร? เมื่อใดจึงควรใช้วิธีการไล่ระดับสีแบบไล่ระดับ?
สมการปกติสำหรับการถดถอยเชิงเส้นคือ —
β=(X T X) -1 . X T Y
โดยที่ Y = β TX เป็นแบบจำลองสำหรับการถดถอยเชิงเส้น
Y คือเป้าหมายหรือตัวแปรตาม
β เป็นเวกเตอร์ของสัมประสิทธิ์การถดถอย ซึ่งได้มาโดยใช้สมการปกติ
X คือเมทริกซ์คุณลักษณะที่มีคุณลักษณะทั้งหมดเป็นคอลัมน์
โปรดทราบว่าคอลัมน์แรกในเมทริกซ์ X ประกอบด้วย 1 ทั้งหมด นี่คือการรวมค่าออฟเซ็ตสำหรับเส้นการถดถอย
การเปรียบเทียบระหว่างเกรเดียนท์โคตรและสมการปกติ:
| โคตรไล่ระดับ | สมการปกติ |
| ต้องการการปรับแต่งไฮเปอร์พารามิเตอร์สำหรับอัลฟ่า (พารามิเตอร์การเรียนรู้) | ไม่จำเป็น |
| มันเป็นกระบวนการวนซ้ำ | เป็นกระบวนการที่ไม่ทำซ้ำ |
| O(kn 2 ) ความซับซ้อนของเวลา | O(n 3 ) ความซับซ้อนของเวลาเนื่องจากการประเมิน X T X |
| ต้องการเมื่อ n มีขนาดใหญ่มาก | ค่อนข้างช้าสำหรับค่า n . จำนวนมาก |
ในที่นี้ ' k ' คือจำนวนสูงสุดของการวนซ้ำสำหรับการลงระดับแบบเกรเดียนท์ และ ' n ' คือจำนวนจุดข้อมูลทั้งหมดในชุดการฝึก
เห็นได้ชัดว่าถ้าเรามีข้อมูลการฝึกจำนวนมาก สมการปกติก็ไม่นิยมใช้ สำหรับค่าน้อยของ ' n ' สมการปกติจะเร็วกว่าการไล่ระดับสีแบบเกรเดียนต์
แมชชีนเลิร์นนิงคืออะไรและเหตุใดจึงสำคัญ
11. คุณเรียกใช้การถดถอยของคุณกับชุดย่อยต่างๆ ของข้อมูล และในแต่ละชุดย่อย ค่าเบต้าสำหรับตัวแปรบางตัวจะแตกต่างกันอย่างมาก มีปัญหาอะไรที่นี่
กรณีนี้แสดงว่าชุดข้อมูลต่างกัน ดังนั้น เพื่อแก้ปัญหานี้ ชุดข้อมูลควรจัดกลุ่มเป็นชุดย่อยที่แตกต่างกัน จากนั้นจึงควรสร้างแบบจำลองแยกกันสำหรับแต่ละคลัสเตอร์ อีกวิธีหนึ่งในการจัดการกับปัญหานี้คือการใช้โมเดลที่ไม่ใช่พารามิเตอร์ เช่น โครงสร้างการตัดสินใจ ซึ่งสามารถจัดการกับข้อมูลที่ต่างกันได้อย่างมีประสิทธิภาพ

12. การถดถอยเชิงเส้นของคุณไม่ทำงานและแสดงว่ามีค่าประมาณที่ดีที่สุดสำหรับค่าสัมประสิทธิ์การถดถอยจำนวนอนันต์ มีอะไรผิดปกติ?
เงื่อนไขนี้เกิดขึ้นเมื่อมีความสัมพันธ์ที่สมบูรณ์แบบ (บวกหรือลบ) ระหว่างตัวแปรบางตัว ในกรณีนี้ ไม่มีค่าเฉพาะสำหรับสัมประสิทธิ์ ดังนั้นเงื่อนไขที่กำหนดจึงเกิดขึ้น
13. คุณหมายถึงอะไรโดยการปรับ R 2 ? ต่างจาก R2 อย่างไร ?
ปรับ R 2 เช่นเดียวกับ R 2 เป็นตัวแทนของจำนวนจุดที่อยู่รอบเส้นการถดถอย นั่นคือมันแสดงให้เห็นว่าโมเดลนั้นเหมาะสมกับข้อมูลการฝึกแค่ไหน สูตรปรับ R 2 เป็น -
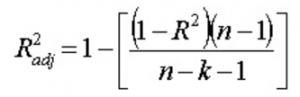
โดยที่ n คือจำนวนจุดข้อมูล และ k คือจำนวนคุณลักษณะ
ข้อเสียเปรียบประการหนึ่งของ R 2 คือมันจะเพิ่มขึ้นด้วยการเพิ่มฟีเจอร์ใหม่อยู่เสมอ ไม่ว่าฟีเจอร์ใหม่จะมีประโยชน์หรือไม่ก็ตาม R 2 . ที่ปรับแล้ว เอาชนะข้อเสียนี้ ค่าของ R 2 ที่ปรับปรุงแล้ว จะเพิ่มขึ้นก็ต่อเมื่อคุณสมบัติที่เพิ่มเข้ามาใหม่มีบทบาทสำคัญในโมเดลเท่านั้น
14. คุณตีความเส้นโค้งมูลค่าคงเหลือเทียบกับค่าพอดีอย่างไร?
แผนภาพมูลค่าคงเหลือเทียบกับค่าพอดีจะใช้เพื่อดูว่าค่าที่คาดการณ์ไว้และค่าคงเหลือมีความสัมพันธ์กันหรือไม่ ถ้าเศษที่เหลือกระจายตามปกติ ด้วยค่าเฉลี่ยรอบค่าที่ติดตั้งและความแปรปรวนคงที่ แบบจำลองของเราทำงานได้ดี มิฉะนั้นจะมีปัญหากับรุ่น
ปัญหาที่พบบ่อยที่สุดที่สามารถพบได้เมื่อฝึกโมเดลในชุดข้อมูลที่หลากหลายคือ heteroscedasticity (อธิบายไว้ในคำตอบด้านล่าง) การมีอยู่ของ heteroscedasticity นั้นสามารถเห็นได้ง่ายโดยการวางแผนกราฟค่าคงเหลือเทียบกับกราฟที่พอดี
15. heteroscedasticity คืออะไร? ผลที่ตามมาคืออะไรและคุณจะเอาชนะมันได้อย่างไร?
ตัวแปรสุ่มเรียกว่า heteroscedastic เมื่อประชากรย่อยต่างกันมีความแปรปรวนต่างกัน (ส่วนเบี่ยงเบนมาตรฐาน)
การมีอยู่ของ heteroscedasticity ทำให้เกิดปัญหาบางอย่างในการวิเคราะห์การถดถอย เนื่องจากข้อสมมติระบุว่าเงื่อนไขข้อผิดพลาดไม่มีความสัมพันธ์กัน ดังนั้น ความแปรปรวนจึงคงที่ การมีอยู่ของ heteroscedasticity มักจะเห็นได้ในรูปแบบของแผนภาพการกระจายแบบรูปกรวยสำหรับค่าที่เหลือและค่าที่พอดี
สมมติฐานพื้นฐานประการหนึ่งของการถดถอยเชิงเส้นคือไม่มีข้อมูล heteroscedasticity เนื่องจากการละเมิดสมมติฐาน ตัวประมาณค่า Ordinary Least Squares (OLS) จึงไม่ใช่ตัวประมาณค่าเชิงเส้นที่ไม่เอนเอียงที่ดีที่สุด (BLUE) ดังนั้นจึงไม่ได้ให้ค่าความแปรปรวนน้อยที่สุดเมื่อเทียบกับตัวประมาณค่าเชิงเส้นที่ไม่เอนเอียง (LUE) อื่นๆ
ไม่มีขั้นตอนตายตัวที่จะเอาชนะความแตกต่างได้ อย่างไรก็ตาม มีบางวิธีที่อาจนำไปสู่การลดความต่างศักย์ลงได้ พวกเขาคือ -
- ลอการิทึมของข้อมูล: อนุกรมที่เพิ่มขึ้นแบบทวีคูณมักส่งผลให้เกิดความแปรปรวนเพิ่มขึ้น สิ่งนี้สามารถเอาชนะได้โดยใช้การแปลงบันทึก
- การใช้การถดถอยเชิงเส้นแบบถ่วงน้ำหนัก: ในที่นี้ วิธี OLS ใช้กับค่าถ่วงน้ำหนักของ X และ Y วิธีหนึ่งคือการแนบน้ำหนักที่เกี่ยวข้องโดยตรงกับขนาดของตัวแปรตาม
16. วีไอเอฟคืออะไร? คุณคำนวณมันได้อย่างไร?
Variance Inflation Factor (VIF) ใช้เพื่อตรวจสอบการมีอยู่ของหลายคอลลิเนียร์ในชุดข้อมูล มันถูกคำนวณเป็น-
ที่นี่ VIF j คือค่าของ VIF สำหรับ ตัวแปร j
Rj2 _ คือค่า R 2 ของโมเดลเมื่อตัวแปรนั้นถดถอยกับตัวแปรอิสระอื่นๆ ทั้งหมด
หากค่าของ VIF สูงสำหรับตัวแปร แสดงว่า R 2 ค่าของแบบจำลองที่สอดคล้องกันสูง กล่าวคือ ตัวแปรอิสระอื่น ๆ สามารถอธิบายตัวแปรนั้นได้ พูดง่ายๆ ก็คือ ตัวแปรนั้นขึ้นอยู่กับตัวแปรอื่นเป็นเส้นตรง
17. คุณรู้ได้อย่างไรว่าการถดถอยเชิงเส้นเหมาะสมกับข้อมูลใด ๆ
หากต้องการดูว่าการถดถอยเชิงเส้นเหมาะสมกับข้อมูลใดๆ หรือไม่ สามารถใช้พล็อตกระจาย ถ้าความสัมพันธ์มีลักษณะเชิงเส้น เราก็สามารถเลือกตัวแบบเชิงเส้นได้ แต่ถ้าไม่ใช่กรณีนี้ เราต้องใช้การแปลงเพื่อสร้างความสัมพันธ์เชิงเส้น การพล็อตพล็อตกระจายนั้นง่ายในกรณีที่มีการถดถอยเชิงเส้นอย่างง่ายหรือไม่มีตัวแปร แต่ในกรณีของการถดถอยเชิงเส้นพหุตัวแปร สามารถพล็อตกราฟแบบกระจายคู่แบบสองมิติ กราฟแบบหมุน และกราฟไดนามิกได้
18. การทดสอบสมมติฐานใช้ในการถดถอยเชิงเส้นอย่างไร
การทดสอบสมมติฐานสามารถทำได้ในการถดถอยเชิงเส้นเพื่อวัตถุประสงค์ดังต่อไปนี้:
- เพื่อตรวจสอบว่าตัวทำนายมีความสำคัญต่อการทำนายของตัวแปรเป้าหมายหรือไม่ สองวิธีทั่วไปสำหรับสิ่งนี้คือ -
- โดยการใช้ค่า p:
หากค่า p ของตัวแปรมากกว่าค่าจำกัดที่กำหนด (โดยปกติคือ 0.05) ตัวแปรนั้นไม่มีนัยสำคัญในการทำนายของตัวแปรเป้าหมาย - โดยการตรวจสอบค่าสัมประสิทธิ์การถดถอย:
หากค่าสัมประสิทธิ์การถดถอยที่สอดคล้องกับตัวทำนายเป็นศูนย์ แสดงว่าตัวแปรนั้นไม่มีนัยสำคัญในการทำนายของตัวแปรเป้าหมายและไม่มีความสัมพันธ์เชิงเส้นกับตัวแปรนั้น
- โดยการใช้ค่า p:
- เพื่อตรวจสอบว่าสัมประสิทธิ์การถดถอยที่คำนวณได้เป็นตัวประมาณที่ดีของสัมประสิทธิ์จริงหรือไม่
19. อธิบายการถดถอยเชิงเกรเดียนต์เกี่ยวกับการถดถอยเชิงเส้น
Gradient Descent เป็นอัลกอริธึมการปรับให้เหมาะสม ในการถดถอยเชิงเส้น ใช้เพื่อเพิ่มประสิทธิภาพฟังก์ชันต้นทุนและค้นหาค่าของ βs (ตัวประมาณ) ที่สอดคล้องกับค่าที่เหมาะสมที่สุดของฟังก์ชันต้นทุน
การไล่ระดับสีทำงานเหมือนลูกบอลกลิ้งไปตามกราฟ (ไม่สนใจความเฉื่อย) ลูกบอลเคลื่อนที่ไปตามทิศทางของการไล่ระดับสูงสุดและหยุดนิ่งที่พื้นผิวเรียบ (minima) 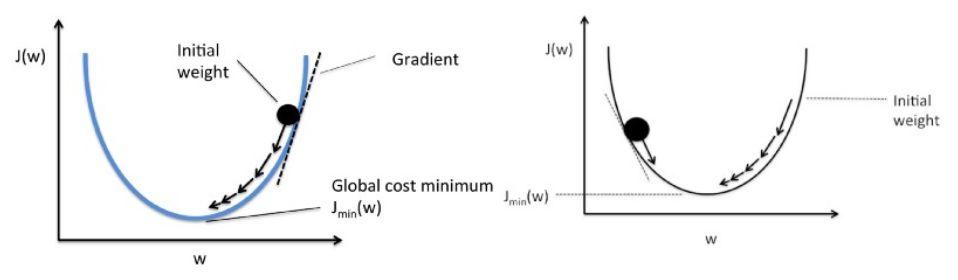
ในทางคณิตศาสตร์ จุดมุ่งหมายของการไล่ระดับการถดถอยเชิงเส้นคือการหาคำตอบของ
ArgMin J(Θ 0 ,Θ 1 ) โดยที่ J(Θ 0 ,Θ 1 ) เป็นฟังก์ชันต้นทุนของการถดถอยเชิงเส้น มอบให้โดย— 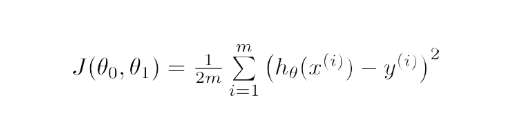
ที่นี่ h คือแบบจำลองสมมติฐานเชิงเส้น h=Θ 0 + Θ 1 x, y คือผลลัพธ์ที่แท้จริง และ m คือจำนวนจุดข้อมูลในชุดการฝึก
Gradient Descent เริ่มต้นด้วยโซลูชันแบบสุ่ม จากนั้นตามทิศทางของการไล่ระดับสี โซลูชันจะได้รับการอัปเดตเป็นค่าใหม่ที่ฟังก์ชันต้นทุนมีค่าต่ำกว่า
การอัปเดตคือ:
ทำซ้ำจนกระทั่งบรรจบกัน 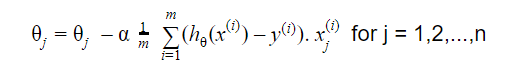
20. คุณตีความแบบจำลองการถดถอยเชิงเส้นอย่างไร?
ตัวแบบการถดถอยเชิงเส้นค่อนข้างง่ายต่อการตีความ โมเดลมีรูปแบบดังต่อไปนี้: 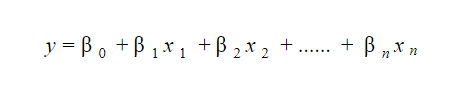
ความสำคัญของแบบจำลองนี้อยู่ในความจริงที่ว่าเราสามารถตีความและเข้าใจการเปลี่ยนแปลงเล็กน้อยและผลที่ตามมาได้อย่างง่ายดาย ตัวอย่างเช่น หากค่าของ x 0 เพิ่มขึ้น 1 หน่วย ทำให้ตัวแปรอื่นๆ คงที่ ค่า y ที่เพิ่มขึ้นทั้งหมด จะเป็น β i ในทางคณิตศาสตร์ ระยะการสกัดกั้น ( β 0 ) คือการตอบสนองเมื่อเงื่อนไขตัวทำนายทั้งหมดถูกตั้งค่าเป็นศูนย์หรือไม่ถูกพิจารณา
เทคนิคการเรียนรู้ด้วยเครื่อง 6 อย่างนี้กำลังปรับปรุงการดูแลสุขภาพ
21. การถดถอยที่แข็งแกร่งคืออะไร?
ตัวแบบการถดถอยควรมีลักษณะที่แข็งแกร่ง ซึ่งหมายความว่าด้วยการเปลี่ยนแปลงในการสังเกตสองสามอย่าง โมเดลไม่ควรเปลี่ยนแปลงอย่างมาก นอกจากนี้ ค่าผิดปกติไม่ควรได้รับผลกระทบมากนัก
แบบจำลองการถดถอยด้วย OLS (Ordinary Least Squares) ค่อนข้างไวต่อค่าผิดปกติ เพื่อแก้ปัญหานี้ เราสามารถใช้วิธี WLS (Weighted Least Squares) เพื่อกำหนดตัวประมาณค่าสัมประสิทธิ์การถดถอย ในที่นี้ ค่าน้ำหนักที่น้อยกว่าจะถูกมอบให้กับค่าผิดปกติหรือจุดเลเวอเรจที่สูงในข้อต่อ ทำให้จุดเหล่านี้ส่งผลกระทบน้อยลง
22. กราฟใดแนะนำให้สังเกตก่อนการปรับโมเดล
ก่อนปรับโมเดลให้เหมาะสม เราต้องทราบข้อมูลเป็นอย่างดี เช่น แนวโน้ม การกระจาย ความเบ้ ฯลฯ ในตัวแปรคืออะไร สามารถใช้กราฟต่างๆ เช่น ฮิสโตแกรม แผนภาพกล่อง และแผนภาพจุดเพื่อสังเกตการกระจายของตัวแปรได้ นอกจากนี้ ยังต้องวิเคราะห์ว่าความสัมพันธ์ระหว่างตัวแปรตามและตัวแปรอิสระคืออะไร สามารถทำได้โดย แปลงแบบกระจาย (ในกรณีที่มีปัญหาแบบไม่มีตัวแปร) แปลงแบบหมุน แปลงแบบไดนามิก ฯลฯ
23. ตัวแบบเชิงเส้นทั่วไปคืออะไร?
ตัว แบบเชิงเส้นทั่วไปเป็นอนุพันธ์ของตัวแบบการถดถอยเชิงเส้นธรรมดา GLM มีความยืดหยุ่นมากกว่าในแง่ของปริมาณสารตกค้าง และสามารถใช้ได้ในกรณีที่การถดถอยเชิงเส้นไม่เหมาะสม GLM ยอมให้การกระจายของที่เหลือเป็นอย่างอื่นนอกเหนือจากการแจกแจงแบบปกติ มันสรุปการถดถอยเชิงเส้นโดยให้ตัวแบบเชิงเส้นเชื่อมโยงไปยังตัวแปรเป้าหมายโดยใช้ฟังก์ชันการเชื่อมโยง การประมาณค่าแบบจำลองทำได้โดยใช้วิธีการประมาณความน่าจะเป็นสูงสุด
24. อธิบายการแลกเปลี่ยนความแปรปรวนอคติ
อคติหมายถึงความแตกต่างระหว่างค่าที่ทำนายโดยแบบจำลองและค่าจริง มันเป็นข้อผิดพลาด เป้าหมายหนึ่งของอัลกอริทึม ML คือการมีอคติต่ำ
ความแปรปรวนหมายถึงความไวของแบบจำลองต่อความผันผวนเล็กน้อยในชุดข้อมูลการฝึก เป้าหมายอีกประการของอัลกอริทึม ML คือการมีความแปรปรวนต่ำ
สำหรับชุดข้อมูลที่ไม่ใช่เชิงเส้นตรงทั้งหมด เป็นไปไม่ได้ที่จะมีอคติและความแปรปรวนต่ำในเวลาเดียวกัน แบบจำลองเส้นตรงจะมีความแปรปรวนต่ำแต่มีความเอนเอียงสูง ในขณะที่พหุนามระดับสูงจะมีอคติต่ำแต่มีความแปรปรวนสูง
ไม่มีการหลีกเลี่ยงความสัมพันธ์ระหว่างอคติและความแปรปรวนในการเรียนรู้ของเครื่อง
- การลดความลำเอียงจะเพิ่มความแปรปรวน
- การลดความแปรปรวนจะเพิ่มอคติ
ดังนั้นจึงมีข้อแลกเปลี่ยนระหว่างคนทั้งสอง ผู้เชี่ยวชาญ ML ต้องตัดสินใจโดยพิจารณาจากปัญหาที่กำหนดว่าจะทนต่ออคติและความแปรปรวนได้มากน้อยเพียงใด ด้วยเหตุนี้ โมเดลสุดท้ายจึงถูกสร้างขึ้น
25. เส้นโค้งการเรียนรู้จะช่วยสร้างแบบจำลองที่ดีขึ้นได้อย่างไร?
เส้นโค้งการเรียนรู้บ่งบอกถึงการสวมใส่มากเกินไปหรือน้อยเกินไป
ในกราฟการเรียนรู้ ข้อผิดพลาดการฝึกอบรมและข้อผิดพลาดในการตรวจสอบข้ามจะถูกพล็อตกับจำนวนจุดข้อมูลการฝึกอบรม เส้นโค้งการเรียนรู้ทั่วไปมีลักษณะดังนี้: 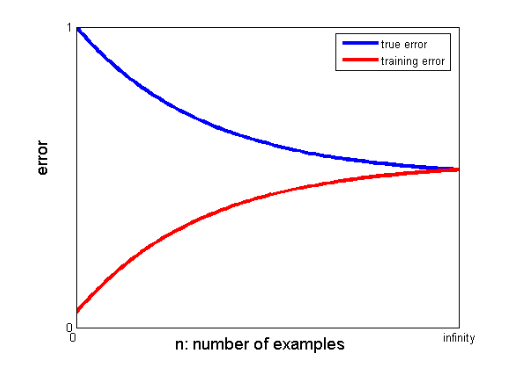
หากข้อผิดพลาดการฝึกอบรมและข้อผิดพลาดที่แท้จริง (ข้อผิดพลาดในการตรวจสอบความถูกต้อง) มาบรรจบกันเป็นค่าเดียวกันและค่าที่สอดคล้องกันของข้อผิดพลาดนั้นสูง แสดงว่าแบบจำลองนั้นไม่เหมาะสมและมีอคติสูง
บทสัมภาษณ์แมชชีนเลิร์นนิงและวิธีเอาชนะพวกเขา
บทสัมภาษณ์ของแมชชีนเลิร์นนิงอาจแตกต่างกันไปตามประเภทหรือหมวดหมู่ เช่น นายหน้าบางคนถาม คำถามสัมภาษณ์ การถดถอยเชิงเส้น หลาย คำถาม เมื่อไปรับบทบาทการสัมภาษณ์วิศวกรแมชชีนเลิร์นนิง พวกเขาสามารถเชี่ยวชาญในหมวดหมู่ต่างๆ เช่น การเข้ารหัส การวิจัย กรณีศึกษา การจัดการโครงการ การนำเสนอ การออกแบบระบบ และสถิติ เราจะเน้นไปที่ประเภทที่พบบ่อยที่สุดและวิธีเตรียมตัวสำหรับหมวดหมู่เหล่านั้น
- การเข้ารหัส
การเข้ารหัสและการเขียนโปรแกรมเป็นองค์ประกอบสำคัญของการสัมภาษณ์แมชชีนเลิร์นนิงและมักใช้เพื่อคัดกรองผู้สมัคร ในการที่จะทำได้ดีในการสัมภาษณ์เหล่านี้ คุณต้องมีความสามารถในการเขียนโปรแกรมที่แข็งแกร่ง การสัมภาษณ์การเข้ารหัสมักใช้เวลาประมาณ 45 ถึง 60 นาทีและประกอบด้วยคำถามเพียงสองข้อเท่านั้น ผู้สัมภาษณ์วางหัวข้อและคาดหวังว่าผู้สมัครจะจัดการเรื่องนี้ให้เร็วที่สุดเท่าที่จะเป็นไปได้
วิธีเตรียมตัว – คุณสามารถเตรียมตัวสำหรับการสัมภาษณ์เหล่านี้ได้โดยต้องมีความเข้าใจที่ดีเกี่ยวกับโครงสร้างข้อมูล ความซับซ้อนของเวลาและพื้นที่ ทักษะการจัดการ และความสามารถในการทำความเข้าใจและแก้ไขปัญหา upGrad มีหลักสูตรวิศวกรรมซอฟต์แวร์ที่ยอดเยี่ยมที่จะช่วยให้คุณพัฒนาทักษะการเขียนโค้ดและฝึกฝนในการสัมภาษณ์ได้
2. การเรียนรู้ของเครื่อง
ความเข้าใจของคุณเกี่ยวกับแมชชีนเลิร์นนิงจะได้รับการประเมินผ่านการสัมภาษณ์ เลเยอร์ Convolutional, โครงข่ายประสาทที่เกิดซ้ำ, เครือข่ายปฏิปักษ์กำเนิด, การรู้จำคำพูด และหัวข้ออื่นๆ อาจครอบคลุมได้ขึ้นอยู่กับความต้องการในการจ้างงาน
วิธีเตรียมตัว – เพื่อให้สามารถเอาชนะการสัมภาษณ์นี้ได้ คุณต้องแน่ใจว่าคุณมีความเข้าใจอย่างถ่องแท้เกี่ยวกับบทบาทและความรับผิดชอบของงาน ซึ่งจะช่วยให้คุณระบุข้อกำหนดของ ML ที่คุณต้องศึกษา อย่างไรก็ตาม หากคุณไม่พบข้อกำหนดใด ๆ คุณต้องเข้าใจพื้นฐานอย่างลึกซึ้ง หลักสูตรเชิงลึกใน ML ที่ upGrad มีให้สามารถช่วยคุณได้ คุณยังสามารถศึกษา บทความ ล่าสุดเกี่ยว กับ ML และ AI เพื่อทำความเข้าใจแนวโน้มล่าสุด และรวมไว้เป็นประจำ
3. คัดกรอง
การสัมภาษณ์นี้ค่อนข้างไม่เป็นทางการและมักเป็นจุดเริ่มต้นหนึ่งของการสัมภาษณ์ นายจ้างที่คาดหวังมักจะจัดการกับมัน เป้าหมายหลักของการสัมภาษณ์ครั้งนี้คือการทำให้ผู้สมัครเข้าใจถึงธุรกิจ บทบาทและหน้าที่ ในบรรยากาศที่เป็นกันเอง ผู้สมัครจะถูกตั้งคำถามเกี่ยวกับอดีตของตนด้วยเพื่อพิจารณาว่าประเด็นที่พวกเขาสนใจตรงกับตำแหน่งหรือไม่
วิธีเตรียมตัว – นี่เป็นส่วนที่ไม่ใช่ด้านเทคนิคของการสัมภาษณ์ ทั้งหมดนี้คือความจริงใจของคุณและพื้นฐานของความเชี่ยวชาญพิเศษของคุณในการเรียนรู้ของเครื่อง
4. การออกแบบระบบ
การสัมภาษณ์ดังกล่าวจะทดสอบความสามารถของบุคคลในการสร้างโซลูชันที่ปรับขนาดได้อย่างเต็มที่ตั้งแต่ต้นจนจบ วิศวกรส่วนใหญ่มักหมกมุ่นอยู่กับปัญหาที่พวกเขามักจะมองข้ามภาพรวม การสัมภาษณ์ออกแบบระบบจำเป็นต้องมีความเข้าใจในองค์ประกอบต่างๆ มากมายที่รวมกันเพื่อสร้างโซลูชัน องค์ประกอบเหล่านี้รวมถึงเลย์เอาต์ส่วนหน้า ตัวโหลดบาลานซ์ แคช และอื่นๆ ระบบ end-to-end ที่มีประสิทธิภาพและปรับขนาดได้จะพัฒนาได้ง่ายขึ้นเมื่อเข้าใจปัญหาเหล่านี้เป็นอย่างดี
วิธีเตรียมตัว – ทำความเข้าใจแนวคิดและส่วนประกอบของโครงการออกแบบระบบ ใช้ตัวอย่างในชีวิตจริงเพื่ออธิบายโครงสร้างให้ผู้สัมภาษณ์เข้าใจโครงการมากขึ้น
บล็อกการเรียนรู้ของเครื่องยอดนิยมและปัญญาประดิษฐ์
| IoT: ประวัติศาสตร์ ปัจจุบัน และอนาคต | บทช่วยสอนการเรียนรู้ของเครื่อง: เรียนรู้ ML | อัลกอริทึมคืออะไร? ง่ายและสะดวก |
| เงินเดือนวิศวกรหุ่นยนต์ในอินเดีย: บทบาททั้งหมด | วันหนึ่งในชีวิตของวิศวกรแมชชีนเลิร์นนิง: พวกเขาทำอะไร? | IoT คืออะไร (Internet of Things) |
| การเปลี่ยนแปลงและการรวมกัน: ความแตกต่างระหว่างการเปลี่ยนแปลงและการรวมกัน | แนวโน้ม 7 อันดับแรกในปัญญาประดิษฐ์และการเรียนรู้ของเครื่อง | แมชชีนเลิร์นนิงกับ R: ทุกสิ่งที่คุณต้องรู้ |

หากมีช่องว่างที่มีนัยสำคัญระหว่างค่าการบรรจบกันของการฝึกอบรมและข้อผิดพลาดการตรวจสอบข้าม กล่าวคือ ข้อผิดพลาดในการตรวจสอบข้ามสูงกว่าข้อผิดพลาดในการฝึกอย่างมีนัยสำคัญ แสดงว่าแบบจำลองมีข้อมูลการฝึกมากเกินไปและมีความแปรปรวนสูง .
วิศวกรการเรียนรู้ของเครื่อง: ตำนานกับความเป็นจริง
นั่นคือจุดสิ้นสุดของส่วนแรกของซีรีส์นี้ ติดตามต่อในตอนต่อไปของซีรี ส์ ซึ่งประกอบด้วยคำถามตาม Logistic Regression รู้สึกอิสระที่จะโพสต์ความคิดเห็นของคุณ
ร่วมเขียนโดย – Ojas Agarwal
คุณสามารถตรวจสอบ Executive PG Program ของเราใน Machine Learning & AI ซึ่ง มีการฝึกอบรมเชิงปฏิบัติ ที่ปรึกษาในอุตสาหกรรมแบบตัวต่อตัว กรณีศึกษาและการมอบหมาย 12 กรณี สถานะศิษย์เก่า IIIT-B และอื่นๆ
คุณเข้าใจอะไรจากการทำให้เป็นมาตรฐาน?
การทำให้เป็นมาตรฐานเป็นกลยุทธ์ในการจัดการกับปัญหาของโมเดลที่มากเกินไป Overfitting เกิดขึ้นเมื่อมีการใช้แบบจำลองที่ซับซ้อนกับข้อมูลการฝึก โมเดลพื้นฐานอาจไม่สามารถสรุปข้อมูลได้ในบางครั้ง และโมเดลที่ซับซ้อนอาจทำให้ข้อมูลมากเกินไป การทำให้เป็นมาตรฐานใช้เพื่อบรรเทาปัญหานี้ การทำให้เป็นมาตรฐานคือกระบวนการของการเพิ่มเงื่อนไขสัมประสิทธิ์ (เบต้า) ให้กับปัญหาการย่อให้เล็กสุดในลักษณะที่เงื่อนไขนั้นถูกลงโทษและมีขนาดพอประมาณ ซึ่งจะช่วยระบุรูปแบบข้อมูลโดยพื้นฐานแล้วในขณะเดียวกันก็ป้องกันการใส่มากเกินไปโดยป้องกันไม่ให้แบบจำลองซับซ้อนเกินไป
คุณเข้าใจอะไรเกี่ยวกับวิศวกรรมคุณลักษณะ
กระบวนการเปลี่ยนข้อมูลดั้งเดิมเป็นคุณลักษณะที่อธิบายปัญหาพื้นฐานของแบบจำลองการคาดการณ์ได้ดีกว่า ส่งผลให้ความถูกต้องของแบบจำลองดีขึ้นในข้อมูลที่มองไม่เห็น เรียกว่าวิศวกรรมคุณลักษณะ ในแง่ของคนธรรมดา วิศวกรรมคุณลักษณะหมายถึงการสร้างคุณลักษณะเพิ่มเติมที่อาจช่วยในการทำความเข้าใจและการสร้างแบบจำลองของปัญหาได้ดีขึ้น วิศวกรรมคุณลักษณะมีสองประเภท: ที่ขับเคลื่อนด้วยธุรกิจและที่ขับเคลื่อนด้วยข้อมูล การรวมคุณสมบัติจากมุมมองทางการค้าเป็นจุดสนใจของวิศวกรรมคุณลักษณะที่ขับเคลื่อนด้วยธุรกิจ
อะไรคือการแลกเปลี่ยนความแปรปรวนอคติ?
ช่องว่างระหว่างแบบจำลอง - ค่าที่คาดการณ์ไว้และค่าจริงเรียกว่าอคติ มันเป็นความผิดพลาด ความเอนเอียงต่ำเป็นหนึ่งในวัตถุประสงค์ของอัลกอริทึม ML ช่องโหว่ของแบบจำลองต่อการเปลี่ยนแปลงเล็กน้อยในชุดข้อมูลการฝึกอบรมเรียกว่าความแปรปรวน ความแปรปรวนต่ำเป็นอีกเป้าหมายหนึ่งของอัลกอริทึม ML เป็นไปไม่ได้ที่จะมีทั้งอคติต่ำและความแปรปรวนต่ำในชุดข้อมูลที่ไม่เป็นเส้นตรงอย่างสมบูรณ์ ความแปรปรวนของแบบจำลองเส้นตรงนั้นต่ำ แต่ความเอนเอียงนั้นใหญ่ ในขณะที่ความแปรปรวนของพหุนามดีกรีสูงนั้นต่ำ แต่ความเอนเอียงนั้นสูง ในแมชชีนเลิร์นนิง จะหลีกเลี่ยงความเชื่อมโยงระหว่างอคติกับความแปรปรวนไม่ได้
