บทนำเกี่ยวกับฟังก์ชันความหนาแน่นของความน่าจะเป็น [สูตร คุณสมบัติ การใช้งาน ตัวอย่าง]

ฟังก์ชันความหนาแน่นของความน่าจะเป็น (PDF) คือนิพจน์ในสถิติที่แสดงถึงการกระจายความน่าจะเป็นของตัวแปรสุ่มแบบไม่ต่อเนื่อง การกระจายความน่าจะเป็น ในแง่ง่ายๆ สามารถกำหนดเป็นความน่าจะเป็นของผลลัพธ์ของตัวแปรสุ่ม เช่น หุ้นหรือ ETF ตัวแปรแบบไม่ต่อเนื่องเกิดขึ้นในทางตรงกันข้ามกับตัวแปรสุ่มอย่างต่อเนื่องซึ่งสามารถกำหนดค่าได้อย่างแม่นยำ

ตัวอย่างเช่น ค่า scrip ในตลาดหุ้นมีจุดทศนิยมเพียงสองจุด (เช่น 65.76) ในตัวแปรสุ่มแบบไม่ต่อเนื่องแทนที่จะเป็นตัวแปรต่อเนื่องที่มีจุดทศนิยมจำนวนเท่าใดก็ได้ (ตัวอย่าง: 65.7685434567)

ฟังก์ชันความหนาแน่นของความน่าจะเป็นเป็นเครื่องมือทางสถิติที่ใช้ในการกำหนดความน่าจะเป็นของผลลัพธ์ของตัวแปรสุ่มแบบไม่ต่อเนื่อง เมื่อพล็อตบนกราฟ PDF จะมีลักษณะเหมือนกับเส้นโค้งรูประฆัง ซึ่งพื้นที่ใต้เส้นโค้งแสดงถึงความน่าจะเป็นของผลลัพธ์

เมื่อฉายเป็นแบบจำลองกราฟิก พื้นที่ใต้เส้นโค้งแสดงถึงช่วงที่ค่าของตัวแปรสุ่มแบบแยกส่วนจะลดลง ดังนั้น พื้นที่ทั้งหมดใต้เส้นโค้งจึงเท่ากับความน่าจะเป็นของผลลัพธ์ของตัวแปร

ฟังก์ชันความหนาแน่นของความน่าจะเป็นสามารถกำหนดความน่าจะเป็นของตัวแปรสุ่มที่อยู่ภายในช่วงค่าที่กำหนด

โดยทั่วไป ฟังก์ชันความหนาแน่นของความน่าจะเป็นจะวิเคราะห์ความเสี่ยงและรายได้ที่อาจเกิดขึ้นจากกองทุนเฉพาะในตลาดหุ้น

เงื่อนไขที่ต้องได้รับความพึงพอใจจากฟังก์ชันให้ถือว่าเป็นฟังก์ชันความหนาแน่นของความน่าจะเป็น

ค่าของตัวแปรแบบไม่ต่อเนื่องสามารถวัดได้อย่างแม่นยำในทางตรงกันข้ามกับตัวแปรแบบต่อเนื่องที่สามารถมีค่าได้ไม่จำกัด ฟังก์ชันใดๆ ควรเป็นไปตามสองเงื่อนไขด้านล่างเพื่อเป็นฟังก์ชันความหนาแน่นของความน่าจะเป็น:

• ค่า f(x) สำหรับแต่ละค่าที่เป็นไปได้ของตัวแปรสุ่มควรเป็นค่าบวก (ไม่ใช่ค่าลบ)
• ค่าอินทิกรัลของพื้นที่ทั้งหมดของเส้นโค้ง (ค่าอินทิกรัลของค่าที่เป็นไปได้ทั้งหมดของตัวแปรสุ่ม) ควรเป็น 1

ความแตกต่างระหว่างฟังก์ชันความหนาแน่นของความน่าจะเป็นและฟังก์ชันการกระจายความน่าจะเป็น

ตัวแปรสุ่มสามารถมีค่าได้หลายค่า คำอธิบายของค่าที่เป็นไปได้แต่ละค่าที่ตัวแปรสุ่มสามารถมีได้เรียกว่าการแจกแจงความน่าจะเป็น

การแจกแจงความน่าจะเป็นให้ชุดของผลลัพธ์และความน่าจะเป็นที่เกี่ยวข้องกัน ฟังก์ชันทางสถิติที่แสดงการแจกแจงความน่าจะเป็นแบบต่อเนื่องเรียกว่าฟังก์ชันความหนาแน่นของความน่าจะเป็น

มีเครื่องมือทางสถิติอื่นที่แสดงถึงการแจกแจงความน่าจะเป็นแบบไม่ต่อเนื่องที่เรียกว่าฟังก์ชันมวลของความน่าจะเป็น ข้อมูลนี้จะให้รายละเอียดเกี่ยวกับผลลัพธ์ที่เป็นไปได้ทั้งหมดและความน่าจะเป็นของผลลัพธ์

นิพจน์สำหรับฟังก์ชันความหนาแน่นของความน่าจะเป็น

หากตัวแปรสุ่มไม่ต่อเนื่อง การแจกแจงความน่าจะเป็นจะเรียกว่าฟังก์ชันมวลของความน่าจะเป็น และหากเป็นตัวแปรต่อเนื่อง การแจกแจงความน่าจะเป็นจะเรียกว่าฟังก์ชันความหนาแน่นของความน่าจะเป็น

PDF ถูกใช้เมื่อตัวแปรสุ่มที่เป็นปัญหามีช่วงของค่าที่เป็นไปได้ การแจกแจงความน่าจะเป็นใช้เพื่อกำหนดค่าที่แน่นอน

ให้ตัวแปรสุ่มแสดงด้วย X ฟังก์ชันความหนาแน่นของความน่าจะเป็น f ของตัวแปรสุ่ม X สามารถแสดงเป็น

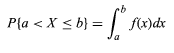
• ค่าของตัวแปรสุ่มอยู่ระหว่าง a และ b
• หาก X หมายถึงความน่าจะเป็นของการเลือกตัวเลขเฉพาะจากช่วง (ช่วง) r และ s แสดงว่าฟังก์ชันความหนาแน่นของความน่าจะเป็นสามารถแสดงเป็น

f ( x ) = 1/( s − r ) สำหรับ r < x < s และ f ( x ) = 0 สำหรับ x < r หรือ x > s

• PDF F แสดงเป็น:

F ( x ) = P { X ≤ x }

ซึ่งเรียกว่าฟังก์ชันการกระจายหรือฟังก์ชันการกระจายสะสมของ X

เมื่อพิจารณาตัวแปรสุ่ม X มีฟังก์ชันการแจกแจงความน่าจะเป็น f ( x ) จากนั้นความสัมพันธ์ระหว่าง f และ F สามารถกำหนดได้เป็น

F ′(. x ) = ฉ ( x )

ฟังก์ชันการกระจายของตัวแปรสุ่มแบบไม่ต่อเนื่องจะแตกต่างจากฟังก์ชันการแจกแจงความน่าจะเป็น ความสัมพันธ์ระหว่างทั้งสองสามารถแสดงได้ดังนี้:

ความคาดหวังของตัวแปรสุ่มแสดงเป็น

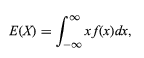
ดังนั้น ตัวแปรที่ไม่ต่อเนื่องและสุ่มทั้งหมดสามารถได้รับการปฏิบัติอย่างสม่ำเสมอด้วยความช่วยเหลือของทฤษฎีที่รวมกัน

สูตรของฟังก์ชันความหนาแน่นของความน่าจะเป็น

ความน่าจะเป็นของตัวแปรสุ่มแบบต่อเนื่อง X บนค่าคงที่บางค่า x จะเป็น 0 เสมอ ในกรณีนี้ จะใช้ P(X = x) ไม่ได้ ควรกำหนดค่าของ X ที่วางอยู่ระหว่างช่วงของค่า (a,b) เพื่อกำหนดเหมือนกันจะใช้สูตรต่อไปนี้

คุณสมบัติของฟังก์ชันความหนาแน่นของความน่าจะเป็น

ตัวแปรสุ่มแบบต่อเนื่องที่ใช้ค่าระหว่างช่วง (a,b) จะถูกประมาณโดยการคำนวณพื้นที่ใต้เส้นโค้งและแกน X ที่พล็อตด้วย (a) เป็นขีดจำกัดล่าง และ (b) เป็นค่าของมัน ขีด จำกัด บน ฟังก์ชันความหนาแน่นของความน่าจะเป็นข้างต้นแสดงเป็น:

ฟังก์ชันความหนาแน่นของความน่าจะเป็นเป็นค่าบวก (ไม่เป็นค่าลบ) สำหรับค่าที่เป็นไปได้ทั้งหมด ซึ่งหมายความว่า f(x)≥ 0 สำหรับทุก ๆ x พื้นที่ตกลงระหว่างเส้นโค้งความหนาแน่นกับแกน X (แกนนอน) เท่ากับ 1

นอกจากนี้ยังสามารถแสดงเป็น:

เส้นโค้งฟังก์ชันความหนาแน่นจะต่อเนื่องตลอดช่วงที่กำหนด ซึ่งกำหนดไว้อย่างชัดเจนเทียบกับชุดค่าต่อเนื่องหรือโดเมนของตัวแปร

เข้าร่วมหลักสูตรแมชชีนเลิร์นนิงออนไลน์จากมหาวิทยาลัยชั้นนำของโลก – ปริญญาโท หลักสูตร Executive Post Graduate และหลักสูตรประกาศนียบัตรขั้นสูงใน ML & AI เพื่อติดตามอาชีพของคุณอย่างรวดเร็ว

การประยุกต์ใช้ฟังก์ชันความหนาแน่นของความน่าจะเป็น

• ฟังก์ชันความหนาแน่นของความน่าจะเป็นถูกใช้ในการสร้างแบบจำลองประจำปีของระดับความเข้มข้น NO ในบรรยากาศ
• แบบจำลองการเผาไหม้ของเครื่องยนต์ดีเซล
• ในสถิติ ฟังก์ชันความหนาแน่นของความน่าจะเป็นใช้เพื่อกำหนดความเป็นไปได้ของผลลัพธ์ของตัวแปรสุ่ม

ตัวอย่างของฟังก์ชันความหนาแน่นของความน่าจะเป็น

• ตัวอย่างที่ 1

ด้านล่างนี้คือตัวอย่างวิธีการใช้ฟังก์ชันความหนาแน่นของความน่าจะเป็น (PDF) เพื่อกำหนดศักยภาพความเสี่ยงของนักลงทุนในตลาดหุ้น:

ประการแรก PDF ถูกสร้างขึ้นเป็นเครื่องมือกราฟิกตามข้อมูลในอดีต

รูปแบบที่พบบ่อยที่สุดของ PDF คือการฉายภาพที่เป็นกลาง ซึ่งความเสี่ยงจะเท่ากับรางวัลในทุกความเป็นไปได้ นักลงทุนที่มีความสามารถในการรับความเสี่ยงน้อยกว่าจะได้รับรางวัลเป็นผลกำไรที่จำกัด และด้วยเหตุนี้จึงมาอยู่ด้านซ้ายของเส้นโค้งรูประฆัง ในทางกลับกัน นักลงทุนที่มีความสามารถในการรับความเสี่ยงสูงมักจะได้รับผลตอบแทนที่สูงขึ้น ดังนั้นจึงตกอยู่ภายใต้ด้านขวาของเส้นโค้ง

นักลงทุนส่วนใหญ่ตกอยู่ภายใต้ความสามารถในการรับความเสี่ยงโดยเฉลี่ย และด้วยเหตุนี้พวกเขาจึงอยู่ตรงกลางของเส้นโค้ง

ซึ่งจะช่วยในการวิเคราะห์ประเภทของนักลงทุนตามข้อมูลที่ได้รับ ซึ่งจะช่วยให้โบรกเกอร์ตลาดหุ้นระบุกลุ่มลูกค้าเป้าหมายที่จะขายผลิตภัณฑ์ของตนได้

• ตัวอย่าง 2

การใช้งานที่สำคัญอย่างหนึ่งของฟังก์ชันความหนาแน่นของความน่าจะเป็นคือตัวแปรสุ่มแบบเกาส์เซียนหรือที่เรียกว่าตัวแปรสุ่มปกติ

ในทั้งสองกรณี กราฟจะให้เส้นโค้งระฆังสำหรับฟังก์ชันความหนาแน่นของความน่าจะเป็น

ความหนาแน่นสามารถแสดงเป็น

กราฟของสมการความหนาแน่นข้างต้นแสดงไว้ด้านล่าง

พื้นที่ใต้เส้นโค้งแสดงถึงค่าจริงของตัวแปรสุ่มแบบเกาส์เซียน

บทสรุป

ฟังก์ชันความหนาแน่นของความน่าจะเป็นมีบทบาทสำคัญในการเรียนรู้ของเครื่อง สำหรับนักเรียนที่กำลังมองหาอาชีพในการเรียนรู้ของเครื่องและปัญญาประดิษฐ์ เราขอแนะนำอย่างยิ่งให้ลงทะเบียนใน โปรแกรมใบรับรองขั้นสูง IIT ของ upGrad ในการเรียนรู้ ของ เครื่อง โปรแกรมนี้ได้รับการปรับแต่งและออกแบบเพื่อให้ผู้ทำงานระดับสูงสามารถปรับใช้โมเดลการเรียนรู้ของเครื่องโดยใช้เทคโนโลยีคลาวด์คอมพิวติ้ง

หลักสูตรนี้ออกแบบโดยคณาจารย์จาก IIT Madras และผู้เชี่ยวชาญในอุตสาหกรรมเพื่อทำให้กระบวนการเรียนรู้มีความเกี่ยวข้องและเป็นประโยชน์มากขึ้น โปรแกรมนำเสนอการรับรองที่เป็นที่ยอมรับทั่วโลกจากวิทยาลัยวิศวกรรมศาสตร์อันดับ 1 และอันดับ 1 ในอินเดียและการสนับสนุนตำแหน่ง 360 องศาจาก upGrad

ยิ่งไปกว่านั้น คุณยังได้รับโอกาสมากมายในการทำงานร่วมกันในโครงการขนาดใหญ่ด้วยฐานผู้เรียนที่จ่ายเงินของ upGrad 40,000+

ตรงไปที่เว็บไซต์ของเราเพื่อเริ่มต้นเส้นทางการเรียนรู้ของคุณ!