บทนำสู่การถดถอยหลายตัวแปรในการเรียนรู้ของเครื่อง: คู่มือฉบับสมบูรณ์

ไม่เป็นความลับที่เทคโนโลยีในปัจจุบันขับเคลื่อนด้วยข้อมูล ข้อมูลอาจเป็นเพียงการรวบรวมตัวเลขเท่านั้น แต่สามารถประมวลผลได้อย่างมีความหมายเพื่อดึงผลิตภาพและทรัพยากรเพื่อให้ธุรกิจสามารถแข่งขันและยั่งยืนได้ในระยะยาว เมื่อเกิดขึ้น การวิเคราะห์ข้อมูลคือคำตอบของการประมาณค่าที่ถูกต้องจากข้อมูลดิบ

การวิเคราะห์ข้อมูลเป็นเทคนิคที่เกี่ยวข้องกับแนวคิดทางสถิติและเชิงตรรกะในการกลั่นกรอง ประมวลผล และแปลงข้อมูลให้อยู่ในรูปแบบที่ใช้งานได้ โซลูชันที่วาดโดยการวิเคราะห์ข้อมูลใช้ในธุรกิจเพื่อทำการตัดสินใจที่สำคัญ วิทยาศาสตร์ข้อมูลพร้อมกับการวิเคราะห์ข้อมูลใช้เพื่อทำนายผลลัพธ์ในอนาคตด้วยความแม่นยำสูง เป็นกระบวนการของการใช้เทคนิคทางวิทยาศาสตร์และอัลกอริธึมในการจัดหาข้อมูลที่เป็นไปได้จากกลุ่มข้อมูล

ปัญหาทั่วไปที่ผู้เชี่ยวชาญด้านข้อมูลต้องเผชิญคือวิธีการตรวจสอบว่ามีความสัมพันธ์ทางสถิติระหว่างตัวแปรตอบสนอง (แสดงโดย Y) และตัวแปรอธิบาย (แสดงโดย Xi) หรือไม่

คำตอบสำหรับข้อกังวลนี้คือการวิเคราะห์การถดถอย มาทำความเข้าใจในรายละเอียดเพิ่มเติมกัน

การวิเคราะห์การถดถอยคืออะไร?

การวิเคราะห์การถดถอยเป็นหนึ่งในวิธียอดนิยมในการวิเคราะห์ข้อมูลที่เป็นไปตามอัลกอริธึมการเรียนรู้ของเครื่องที่มีการควบคุมหรืออยู่ภายใต้การควบคุม เป็นเทคนิคที่มีประสิทธิภาพในการระบุและสร้างความสัมพันธ์ระหว่างตัวแปรในข้อมูล

การวิเคราะห์การถดถอยเกี่ยวข้องกับการคัดแยกตัวแปรที่ทำงานได้โดยใช้กลยุทธ์ทางคณิตศาสตร์เพื่อสรุปผลที่แม่นยำสูงเกี่ยวกับตัวแปรที่จัดเรียงเหล่านั้น

การถดถอยหลายตัวแปรคืออะไร?

ตัวแปรหลายตัวแปรคืออัลกอริธึมการเรียนรู้ของเครื่องที่มีการควบคุมหรืออยู่ภายใต้การควบคุม ซึ่งจะวิเคราะห์ตัวแปรข้อมูลหลายตัว เป็นความต่อเนื่องของการถดถอยพหุคูณที่เกี่ยวข้องกับตัวแปรตามหนึ่งตัวแปรและตัวแปรอิสระหลายตัว ผลลัพธ์ถูกทำนายตามจำนวนของตัวแปรอิสระ

การถดถอยหลายตัวแปรจะคำนวณสูตรที่อธิบายการตอบสนองพร้อมกันของปัจจัยที่มีอยู่ในตัวแปรต่อการเปลี่ยนแปลงของตัวแปรอื่นๆ ใช้เพื่อศึกษาข้อมูลในด้านต่างๆ ตัวอย่างเช่น ในการถดถอยพหุตัวแปรของอสังหาริมทรัพย์ใช้เพื่อคาดการณ์ราคาบ้านโดยพิจารณาจากปัจจัยหลายประการ เช่น ที่ตั้ง จำนวนห้อง และสิ่งอำนวยความสะดวกที่มีอยู่

ฟังก์ชันต้นทุนในการถดถอยหลายตัวแปร

ฟังก์ชันต้นทุนจัดสรรต้นทุนให้กับกลุ่มตัวอย่าง เมื่อผลลัพธ์ของแบบจำลองเบี่ยงเบนไปจากข้อมูลที่สังเกตได้ สมการของฟังก์ชันต้นทุนคือผลรวมของกำลังสองของผลต่างระหว่างค่าที่คาดการณ์กับมูลค่าจริงหารด้วยความยาวของชุดข้อมูลสองเท่า

นี่คือ ตัวอย่าง :

ผลลัพธ์ :

แหล่งที่มา

จะใช้การวิเคราะห์การถดถอยหลายตัวแปรได้อย่างไร

กระบวนการที่เกี่ยวข้องกับการวิเคราะห์การถดถอยพหุตัวแปร ได้แก่ การเลือกคุณลักษณะ วิศวกรรมคุณลักษณะ การทำให้เป็นมาตรฐานของคุณลักษณะ ฟังก์ชันการสูญเสียการเลือก การวิเคราะห์สมมติฐาน และการสร้างแบบจำลองการถดถอย

1. การเลือกคุณสมบัติ: เป็นขั้นตอนที่สำคัญที่สุดในการถดถอยพหุตัวแปร หรือที่เรียกว่าการเลือกตัวแปร กระบวนการนี้เกี่ยวข้องกับการเลือกตัวแปรที่ทำงานได้เพื่อสร้างแบบจำลองที่มีประสิทธิภาพ
2. การทำให้เป็นมาตรฐานของ คุณลักษณะ: สิ่งนี้เกี่ยวข้องกับการปรับขนาดคุณลักษณะเพื่อรักษาการกระจายและอัตราส่วนข้อมูลที่มีความคล่องตัว ซึ่งจะช่วยในการวิเคราะห์ข้อมูลได้ดีขึ้น ค่าของคุณสมบัติทั้งหมดสามารถเปลี่ยนแปลงได้ตามความต้องการ
3. การเลือกฟังก์ชันการสูญเสียและสมมติฐาน : ฟังก์ชันการสูญเสียจะใช้สำหรับการทำนายข้อผิดพลาด ฟังก์ชันการสูญเสียจะมีผลเมื่อการทำนายสมมติฐานเปลี่ยนจากตัวเลขจริง ในที่นี้ สมมติฐานแสดงถึงค่าที่ทำนายจากคุณลักษณะหรือตัวแปร
4. การแก้ไขพารามิเตอร์สมมติฐาน : พารามิเตอร์ของสมมติฐานได้รับการแก้ไขหรือตั้งค่าในลักษณะที่จะลดฟังก์ชันการสูญเสียและปรับปรุงการทำนายที่ดีขึ้น
5. การลดการสูญเสียฟังก์ชัน : ฟังก์ชันการสูญเสียจะลดลงโดยการสร้างอัลกอริธึมเฉพาะสำหรับการลดการสูญเสียในชุดข้อมูล ซึ่งจะช่วยอำนวยความสะดวกในการเปลี่ยนแปลงพารามิเตอร์สมมติฐาน Gradient Descent เป็นอัลกอริธึมที่ใช้กันมากที่สุดสำหรับการลดการสูญเสีย อัลกอริธึมยังสามารถใช้สำหรับการดำเนินการอื่น ๆ เมื่อการลดการสูญเสียเสร็จสมบูรณ์
6. การวิเคราะห์ฟังก์ชันสมมติฐาน : ต้องมีการวิเคราะห์ฟังก์ชันของสมมติฐาน เนื่องจากจำเป็นต่อการทำนายค่าต่างๆ หลังจากวิเคราะห์ฟังก์ชันแล้ว จะทดสอบกับข้อมูลทดสอบ

ให้เรามาดูสองวิธีที่สามารถใช้การถดถอยหลายตัวแปรได้

1. การถดถอยเชิงเส้นหลายตัวแปร

การถดถอยเชิงเส้นแบบหลายตัวแปรคล้ายกับการถดถอยเชิงเส้นอย่างง่าย ยกเว้นว่าในการถดถอยเชิงเส้นหลายตัวแปร ตัวแปรอิสระหลายตัวมีส่วนทำให้เกิดตัวแปรตาม ดังนั้นสัมประสิทธิ์หลายตัวจึงถูกนำมาใช้ในการคำนวณ

• ใช้เพื่อหาความสัมพันธ์ทางคณิตศาสตร์ระหว่างตัวแปรสุ่มหลายตัว อธิบายจำนวนตัวแปรอิสระหลายตัวที่สัมพันธ์กับตัวแปรตามหนึ่งตัวแปร
• รายละเอียดของตัวแปรอิสระหลายตัวจะใช้ในการคาดการณ์ที่แม่นยำถึงอิทธิพลที่มีต่อตัวแปรผลลัพธ์
• ตัวแบบการถดถอยเชิงเส้นแบบหลายตัวแปรสร้างความสัมพันธ์ในรูปแบบเชิงเส้น (รูปแบบของเส้นตรง) โดยมีค่าประมาณที่ดีที่สุดของจุดข้อมูลแต่ละจุด
• สมการของตัวแบบการถดถอยเชิงเส้นหลายตัวแปรคือ:

yi​=β0​+β1​xi1​+β2​xi2​+…+βp​xip​+

โดยที่ สำหรับการสังเกต i=n:

แหล่งที่มา

สามารถใช้การถดถอยเชิงเส้นได้เมื่อใด

ตัวแบบการถดถอยเชิงเส้นสามารถใช้ได้เฉพาะเมื่อมีตัวแปรต่อเนื่องสองตัวซึ่งตัวหนึ่งขึ้นอยู่กับและอีกตัวหนึ่งเป็นอิสระ

ตัวแปรอิสระใช้เป็นพารามิเตอร์ในการกำหนดค่าหรือผลลัพธ์ของตัวแปรตาม

2. การถดถอยโลจิสติกหลายตัวแปร

การถดถอยโลจิสติกเป็นอัลกอริธึมที่ใช้ในการทำนายผลลัพธ์ไบนารีโดยพิจารณาจากตัวแปรอิสระหลายตัว ผลลัพธ์ไบนารีมีความเป็นไปได้สองอย่าง สถานการณ์เกิดขึ้น (แสดงโดย 1) หรือไม่เกิดขึ้น (แสดงด้วย 0)

ใช้การถดถอยโลจิสติกในขณะที่ทำงานกับข้อมูลไบนารี ข้อมูลที่ผลลัพธ์ (หรือตัวแปรตาม) เป็นแบบขั้ว

สามารถใช้การถดถอยโลจิสติกได้ที่ไหน?

การถดถอยโลจิสติกใช้เพื่อจัดการกับปัญหาการจำแนกประเภทเป็นหลัก ตัวอย่างเช่น เพื่อตรวจสอบว่าอีเมลเป็นสแปมหรือไม่ และธุรกรรมนั้นเป็นอันตรายหรือไม่ ในการวิเคราะห์ข้อมูล ใช้ในการตัดสินใจคำนวณเพื่อลดการสูญเสียและเพิ่มผลกำไร

การถดถอยโลจิสติกหลายตัวแปรจะใช้เมื่อมีตัวแปรตามหนึ่งตัวแปรและหลายผลลัพธ์ มันแตกต่างจากการถดถอยโลจิสติกโดยมีผลลัพธ์ที่เป็นไปได้มากกว่าสองรายการ

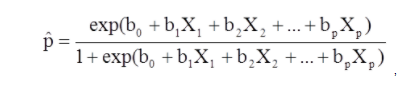
X1 ถึง Xp เป็นตัวแปรอิสระที่แตกต่างกัน

b0 ถึง bp คือสัมประสิทธิ์การถดถอย

แบบจำลองการถดถอยโลจิสติกพหุคูณสามารถเขียนในรูปแบบอื่นได้เช่นกัน ในแบบฟอร์มด้านล่าง ผลลัพธ์คือบันทึกที่คาดหวังของอัตราต่อรองที่ผลลัพธ์มีอยู่

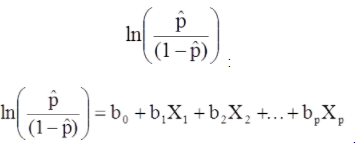
แบบจำลองการถดถอยโลจิสติกพหุคูณสามารถเขียนในรูปแบบอื่นได้เช่นกัน ในแบบฟอร์มด้านล่าง ผลลัพธ์คือบันทึกที่คาดหวังของอัตราต่อรองที่ผลลัพธ์มีอยู่

ทางด้านขวาของสมการข้างต้นคล้ายกับสมการถดถอยเชิงเส้น แต่วิธีการหาค่าสัมประสิทธิ์การถดถอยนั้นแตกต่างกัน

สมมติฐานในแบบจำลองการถดถอยหลายตัวแปร

• ตัวแปรตามและตัวแปรอิสระมีความสัมพันธ์เชิงเส้น
• ตัวแปรอิสระไม่มีความสัมพันธ์ที่ชัดเจนระหว่างกัน
• การสังเกตของ yi ถูกเลือกแบบสุ่มและเป็นรายบุคคลจากประชากร

สมมติฐานในแบบจำลองการถดถอยโลจิสติกหลายตัวแปร

• ตัวแปรตามคือ nominal หรือ ordinal ตัวแปรที่ระบุมีตั้งแต่สองหมวดหมู่ขึ้นไปโดยไม่มีการจัดระเบียบที่มีความหมาย ตัวแปรลำดับสามารถมีได้ตั้งแต่ 2 หมวดหมู่ขึ้นไป แต่มีโครงสร้างและสามารถจัดลำดับได้
• ตัวแปรอิสระตัวแปรเดียวหรือหลายตัวแปรอาจเป็นลำดับ ต่อเนื่อง หรือระบุก็ได้ ตัวแปรต่อเนื่องคือตัวแปรที่สามารถมีค่าอนันต์ภายในช่วงที่กำหนด
• ตัวแปรตามนั้นแยกจากกันและละเอียดถี่ถ้วน
• ตัวแปรอิสระไม่มีความสัมพันธ์ที่ชัดเจนระหว่างกัน

ข้อดีของการถดถอยหลายตัวแปร

1. การถดถอยหลายตัวแปรช่วยให้เราศึกษาความสัมพันธ์ระหว่างตัวแปรหลายตัวในชุดข้อมูล
2. ความสัมพันธ์ระหว่างตัวแปรตามและตัวแปรอิสระช่วยในการทำนายผลลัพธ์
3. เป็นหนึ่งในอัลกอริธึมที่สะดวกและเป็นที่นิยมที่สุดในการเรียนรู้ของเครื่อง

ข้อเสียของการถดถอยหลายตัวแปร

• ความซับซ้อนของเทคนิคพหุตัวแปรต้องอาศัยการคำนวณทางคณิตศาสตร์ที่ซับซ้อน
• การตีความผลลัพธ์ของแบบจำลองการถดถอยหลายตัวแปรไม่ใช่เรื่องง่าย เนื่องจากมีความไม่สอดคล้องกันในผลลัพธ์การสูญเสียและข้อผิดพลาด
• ไม่สามารถใช้ตัวแบบการถดถอยหลายตัวแปรกับชุดข้อมูลที่มีขนาดเล็กกว่าได้ ออกแบบมาเพื่อสร้างเอาต์พุตที่แม่นยำสำหรับชุดข้อมูลขนาดใหญ่

หากคุณต้องการเรียนรู้เพิ่มเติมเกี่ยวกับการถดถอยหลายตัวแปรและวิชาวิทยาศาสตร์ข้อมูลที่ซับซ้อน upGrad มีคำตอบให้คุณ หลักสูตรวิทยาศาสตรมหาบัณฑิตสาขาวิทยาศาสตร์ข้อมูล 18 เดือนของเรา จากมหาวิทยาลัย Liverpool John Moores ครอบคลุมชั่วโมงการเรียนรู้ที่เข้มงวดมากกว่า 500 ชั่วโมง การฝึกสอน 25 ครั้ง (จัดขึ้นแบบ 1:8) และเซสชันสดมากกว่า 20 ครั้ง upGrad ยังเสนอความช่วยเหลือด้านการสอนแบบ 1:1 และการสนับสนุนการแนะแนวอาชีพแบบ 360° สำหรับนักเรียนในการเปลี่ยนแปลงอาชีพของตน ผู้เรียนสามารถใช้การเรียนรู้แบบ Peer-to-Peer บนแพลตฟอร์มระดับโลกด้วยผู้เรียนที่ชำระเงินแล้วกว่า 40,000 คน และทำงานในโครงการร่วมกันใน 6 สาขาวิชาเฉพาะทางเพื่อเพิ่มประสบการณ์การเรียนรู้สูงสุด