Gradient Descent ในการเรียนรู้ของเครื่อง: มันทำงานอย่างไร

บทนำ

ส่วนที่สำคัญที่สุดอย่างหนึ่งของแมชชีนเลิร์นนิงคือการเพิ่มประสิทธิภาพอัลกอริทึม อัลกอริทึมเกือบทั้งหมดใน Machine Learning มีอัลกอริธึมการปรับให้เหมาะสมที่ฐานซึ่งทำหน้าที่เป็นแกนหลักของอัลกอริทึม อย่างที่เราทราบกันดีว่าการเพิ่มประสิทธิภาพเป็นเป้าหมายสูงสุดของอัลกอริธึมใดๆ แม้แต่กับเหตุการณ์ในชีวิตจริงหรือเมื่อต้องรับมือกับผลิตภัณฑ์ที่ใช้เทคโนโลยีในตลาด

ปัจจุบันมีอัลกอริธึมการปรับให้เหมาะสมจำนวนมากที่ใช้ในแอพพลิเคชั่นต่างๆ เช่น การจดจำใบหน้า รถยนต์ที่ขับด้วยตนเอง การวิเคราะห์ตามตลาด ฯลฯ ในทำนองเดียวกันในการเรียนรู้ของเครื่อง อัลกอริธึมการปรับให้เหมาะสมนั้นมีบทบาทสำคัญ อัลกอริธึมการปรับให้เหมาะสมที่ใช้กันอย่างแพร่หลายอย่างหนึ่งคืออัลกอริธึม Gradient Descent ซึ่งเราจะพูดถึงในบทความนี้

Gradient Descent คืออะไร?

ในการเรียนรู้ด้วยเครื่อง อัลกอริธึม Gradient Descent เป็นหนึ่งในอัลกอริธึมที่ใช้กันมากที่สุด แต่ก็ยังทำให้ผู้มาใหม่ส่วนใหญ่ต้องตะลึง ในทางคณิตศาสตร์ Gradient Descent เป็นอัลกอริธึมการเพิ่มประสิทธิภาพแบบวนซ้ำอันดับแรกที่ใช้เพื่อค้นหาค่าต่ำสุดของฟังก์ชันดิฟเฟอเรนติเอได้ พูดง่ายๆ ก็คือ อัลกอริธึม Gradient Descent นี้ใช้เพื่อค้นหาค่าของพารามิเตอร์ของฟังก์ชัน (หรือสัมประสิทธิ์) ซึ่งใช้เพื่อลดฟังก์ชัน cost ให้น้อยที่สุด ฟังก์ชันต้นทุนใช้ในการหาจำนวนข้อผิดพลาดระหว่างค่าที่คาดการณ์ไว้และมูลค่าจริงของแบบจำลอง Machine Learning ที่สร้างขึ้น

สัญชาตญาณการไล่ระดับสี

พิจารณาชามขนาดใหญ่ที่คุณมักจะเก็บผลไม้หรือกินซีเรียล ชามนี้จะเป็นฟังก์ชันต้นทุน (f)

ตอนนี้ พิกัดแบบสุ่มบนส่วนใดๆ ของพื้นผิวชามจะเป็นค่าปัจจุบันของสัมประสิทธิ์ของฟังก์ชันต้นทุน ด้านล่างของโถเป็นชุดค่าสัมประสิทธิ์ที่ดีที่สุดและเป็นค่าต่ำสุดของฟังก์ชัน

ในที่นี้ เป้าหมายคือการคำนวณค่าต่างๆ ของสัมประสิทธิ์ในการวนซ้ำแต่ละครั้ง ประเมินต้นทุนและเลือกสัมประสิทธิ์ที่มีค่าฟังก์ชันต้นทุนที่ดีกว่า (ค่าที่ต่ำกว่า) ในการทำซ้ำหลายครั้ง จะพบว่าด้านล่างของโถมีค่าสัมประสิทธิ์ที่ดีที่สุดในการลดฟังก์ชันต้นทุนให้เหลือน้อยที่สุด

ด้วยวิธีนี้ อัลกอริธึม Gradient Descent จะทำงานเพื่อส่งผลให้มีต้นทุนขั้นต่ำ

เข้าร่วม หลักสูตรแมชชีนเลิ ร์นนิง ออนไลน์จากมหาวิทยาลัยชั้นนำของโลก – ปริญญาโท หลักสูตร Executive Post Graduate และหลักสูตรประกาศนียบัตรขั้นสูงใน ML & AI เพื่อติดตามอาชีพของคุณอย่างรวดเร็ว

ขั้นตอนการไล่ระดับสี

กระบวนการไล่ระดับการลงระดับนี้เริ่มต้นด้วยการจัดสรรค่าเริ่มต้นให้กับสัมประสิทธิ์ของฟังก์ชันต้นทุน นี่อาจเป็นค่าที่ใกล้เคียงกับ 0 หรือค่าสุ่มเล็กน้อย

ค่าสัมประสิทธิ์ = 0.0

ต่อไป ต้นทุนของสัมประสิทธิ์จะได้มาโดยนำไปใช้กับฟังก์ชันต้นทุนและคำนวณต้นทุน

ต้นทุน = f(สัมประสิทธิ์)

จากนั้นจะคำนวณอนุพันธ์ของฟังก์ชันต้นทุน อนุพันธ์ของฟังก์ชันต้นทุนนี้ได้มาจากแนวคิดทางคณิตศาสตร์ของแคลคูลัสเชิงอนุพันธ์ มันทำให้เรามีความชันของฟังก์ชัน ณ จุดที่กำหนดซึ่งคำนวณอนุพันธ์ของมัน ความชันนี้จำเป็นต้องทราบทิศทางที่จะย้ายสัมประสิทธิ์ในการวนซ้ำครั้งต่อไปเพื่อให้ได้มูลค่าต้นทุนที่ต่ำลง ทำได้โดยการสังเกตเครื่องหมายของอนุพันธ์ที่คำนวณได้

เดลต้า = อนุพันธ์ (ต้นทุน)

เมื่อเราทราบทิศทางที่ตกต่ำจากอนุพันธ์ที่คำนวณแล้ว เราจำเป็นต้องอัปเดตค่าสัมประสิทธิ์ สำหรับสิ่งนี้ พารามิเตอร์เรียกว่าพารามิเตอร์การเรียนรู้ โดยจะใช้อัลฟา (α) ค่านี้ใช้เพื่อควบคุมว่าค่าสัมประสิทธิ์สามารถเปลี่ยนแปลงได้มากน้อยเพียงใดทุกครั้งที่มีการอัพเดท

สัมประสิทธิ์ = สัมประสิทธิ์ – (อัลฟา * เดลต้า)

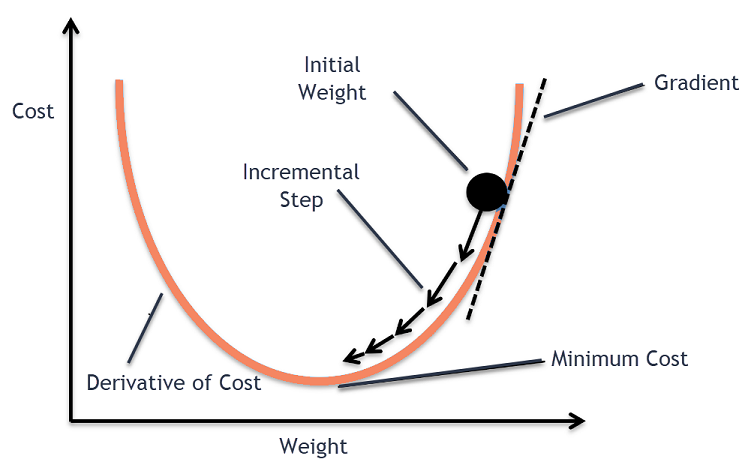
แหล่งที่มา

ด้วยวิธีนี้ กระบวนการนี้จะทำซ้ำจนกว่าต้นทุนของสัมประสิทธิ์จะเท่ากับ 0.0 หรือใกล้พอที่จะเป็นศูนย์ นี่คือขั้นตอนสำหรับอัลกอริธึมการไล่ระดับสีแบบเกรเดียนท์

ประเภทของอัลกอริธึมการไล่ระดับสี

ในยุคปัจจุบัน Gradient Descent มีสามประเภทพื้นฐานที่ใช้ในการเรียนรู้ของเครื่องสมัยใหม่และอัลกอริธึมการเรียนรู้เชิงลึก ความแตกต่างที่สำคัญระหว่างทั้ง 3 ประเภทนี้คือต้นทุนและประสิทธิภาพในการคำนวณ ขึ้นอยู่กับปริมาณข้อมูลที่ใช้ ความซับซ้อนของเวลา และความแม่นยำ มีสามประเภทดังต่อไปนี้

1. Batch Gradient Descent
2. Stochastic Gradient Descent
3. โคตรไล่ระดับมินิแบทช์

Batch Gradient Descent

นี่เป็นเวอร์ชันแรกและเป็นเวอร์ชันพื้นฐานของอัลกอริธึม Gradient Descent ซึ่งชุดข้อมูลทั้งหมดถูกใช้ในคราวเดียวเพื่อคำนวณฟังก์ชันต้นทุนและการไล่ระดับสี เนื่องจากชุดข้อมูลทั้งหมดถูกใช้ในครั้งเดียวสำหรับการอัปเดตครั้งเดียว การคำนวณการไล่ระดับสีในประเภทนี้จึงอาจช้ามากและไม่สามารถทำได้กับชุดข้อมูลที่มีความจุหน่วยความจำไม่เพียงพอของอุปกรณ์

ดังนั้น อัลกอริธึม Batch Gradient Descent นี้จึงใช้สำหรับชุดข้อมูลที่มีขนาดเล็กกว่าเท่านั้น และเมื่อตัวอย่างการฝึกมีจำนวนมาก จะไม่ต้องการการไล่ระดับการไล่ระดับแบบแบทช์ แต่จะใช้อัลกอริธึม Stochastic และ Mini Batch Gradient Descent แทน

Stochastic Gradient Descent

นี่เป็นอัลกอริธึมการไล่ระดับสีแบบเกรเดียนต์อีกประเภทหนึ่งซึ่งมีการประมวลผลตัวอย่างการฝึกเพียงตัวอย่างเดียวเท่านั้นต่อการวนซ้ำ ในขั้นตอนนี้ ขั้นตอนแรกคือการสุ่มชุดข้อมูลการฝึกทั้งหมด จากนั้น ใช้ตัวอย่างการฝึกอบรมเพียงตัวอย่างเดียวในการอัพเดทสัมประสิทธิ์ ซึ่งตรงกันข้ามกับ Batch Gradient Descent ซึ่งพารามิเตอร์ (สัมประสิทธิ์) จะได้รับการอัปเดตก็ต่อเมื่อตัวอย่างการฝึกอบรมทั้งหมดได้รับการประเมินเท่านั้น

Stochastic Gradient Descent (SGD) มีข้อได้เปรียบที่การอัพเดทบ่อยครั้งประเภทนี้จะให้อัตราการปรับปรุงโดยละเอียด อย่างไรก็ตาม ในบางกรณี การดำเนินการนี้อาจมีราคาแพงในการคำนวณ เนื่องจากจะประมวลผลเพียงตัวอย่างเดียวในทุกๆ การวนซ้ำ ซึ่งอาจทำให้จำนวนการวนซ้ำมีขนาดใหญ่มาก

โคตรไล่ระดับมินิแบทช์

นี่เป็นอัลกอริธึมที่พัฒนาขึ้นเมื่อเร็ว ๆ นี้ซึ่งเร็วกว่าอัลกอริธึม Batch และ Stochastic Gradient Descent เป็นที่นิยมมากที่สุดเนื่องจากเป็นการผสมผสานระหว่างอัลกอริธึมที่กล่าวถึงก่อนหน้านี้ ในการดำเนินการนี้ จะแยกชุดการฝึกออกเป็นชุดย่อยหลายชุด และดำเนินการอัปเดตสำหรับแต่ละชุดงานเหล่านี้หลังจากคำนวณการไล่ระดับของชุดงานนั้น (เช่น ในสกุลเงิน SGD)

โดยทั่วไป ขนาดแบทช์จะแตกต่างกันระหว่าง 30 ถึง 500 แต่ไม่มีขนาดตายตัวเนื่องจากจะแตกต่างกันไปตามการใช้งานที่แตกต่างกัน ดังนั้น แม้ว่าจะมีชุดข้อมูลการฝึกอบรมจำนวนมาก แต่อัลกอริธึมนี้จะประมวลผลในชุดย่อย 'b' ดังนั้นจึงเหมาะสำหรับชุดข้อมูลขนาดใหญ่ที่มีจำนวนการวนซ้ำน้อยกว่า

ถ้า 'm' คือจำนวนตัวอย่างการฝึก ถ้า b==m Mini Batch Gradient Descent จะคล้ายกับอัลกอริธึม Batch Gradient Descent

ตัวแปรของการไล่ระดับสีในการเรียนรู้ของเครื่อง

ด้วยพื้นฐานนี้สำหรับ Gradient Descent มีอัลกอริธึมอื่นๆ อีกหลายตัวที่ได้รับการพัฒนาจากสิ่งนี้ บางส่วนของพวกเขาสรุปได้ด้านล่าง

Vanilla Gradient Descent

นี่เป็นหนึ่งในรูปแบบที่ง่ายที่สุดของเทคนิค Gradient Descent ชื่อ วนิลา หมายถึง บริสุทธิ์หรือปราศจากสิ่งเจือปน ในการนี้ ขั้นตอนเล็กๆ จะถูกนำไปในทิศทางของค่าต่ำสุดโดยการคำนวณการไล่ระดับของฟังก์ชันต้นทุน คล้ายกับอัลกอริธึมที่กล่าวถึงข้างต้น กฎการอัพเดทกำหนดโดย

สัมประสิทธิ์ = สัมประสิทธิ์ – (อัลฟา * เดลต้า)

โคตรไล่ระดับด้วยโมเมนตัม

ในกรณีนี้ อัลกอริธึมทำให้เรารู้ขั้นตอนก่อนหน้าก่อนที่จะทำขั้นตอนต่อไป ซึ่งทำได้โดยการแนะนำคำศัพท์ใหม่ซึ่งเป็นผลคูณของการอัปเดตครั้งก่อนและค่าคงที่ที่เรียกว่าโมเมนตัม ในที่นี้ กฎการอัพเดตน้ำหนักจะได้รับโดย

อัปเดต = อัลฟ่า * เดลต้า

ความเร็ว = Previous_update * โมเมนตัม

สัมประสิทธิ์ = สัมประสิทธิ์ + ความเร็ว – อัปเดต

ADAGRAD

คำว่า ADAGRAD ย่อมาจาก Adaptive Gradient Algorithm ตามชื่อของมัน มันใช้เทคนิคที่ปรับเปลี่ยนได้เพื่ออัปเดตตุ้มน้ำหนัก อัลกอริทึมนี้เหมาะสำหรับข้อมูลที่กระจัดกระจายมากกว่า การเพิ่มประสิทธิภาพนี้จะเปลี่ยนอัตราการเรียนรู้ตามความถี่ของการอัปเดตพารามิเตอร์ระหว่างการฝึกอบรม ตัวอย่างเช่น พารามิเตอร์ที่มีการไล่ระดับสีสูงกว่าจะมีอัตราการเรียนรู้ที่ช้าลง เพื่อที่เราจะได้ไม่จบลงด้วยค่าต่ำสุดที่เกินเลยไป ในทำนองเดียวกัน การไล่ระดับสีที่ต่ำกว่าจะมีอัตราการเรียนรู้ที่เร็วขึ้นเพื่อให้ฝึกฝนได้เร็วยิ่งขึ้น

ADAM

อัลกอริธึมการปรับให้เหมาะสมอีกแบบหนึ่งที่มีรากฐานมาจากอัลกอริธึม Gradient Descent คือ ADAM ซึ่งย่อมาจาก Adaptive Moment Estimation เป็นการผสมผสานระหว่าง ADAGRAD และ SGD กับอัลกอริธึมโมเมนตัม มันถูกสร้างขึ้นจากอัลกอริธึม ADAGRAD และถูกสร้างด้านลบเพิ่มเติม ในแง่ง่ายๆ ADAM = ADAGRAD + โมเมนตัม

ด้วยวิธีนี้ อัลกอริธึม Gradient Descent มีรูปแบบอื่นๆ อีกหลายแบบที่ได้รับการพัฒนาและกำลังพัฒนาในโลก เช่น AMSGrad, ADAMax

บทสรุป

ในบทความนี้ เราได้เห็นอัลกอริธึมที่อยู่เบื้องหลังหนึ่งในอัลกอริธึมการปรับให้เหมาะสมที่ใช้บ่อยที่สุดในการเรียนรู้ของเครื่อง นั่นคืออัลกอริธึม Gradient Descent พร้อมด้วยประเภทและตัวแปรที่ได้รับการพัฒนา

upGrad จัดให้มี Executive PG Program ใน Machine Learning & AI และ Master of Science in Machine Learning & AI ที่อาจแนะนำคุณสู่การสร้างอาชีพ หลักสูตรเหล่านี้จะอธิบายความจำเป็นในการเรียนรู้ของเครื่องและขั้นตอนเพิ่มเติมในการรวบรวมความรู้ในโดเมนนี้ ซึ่งครอบคลุมแนวคิดที่หลากหลายตั้งแต่ Gradient Descent ในการเรียนรู้ของเครื่อง