Gaussian Naive Bayes: สิ่งที่คุณต้องรู้?
เผยแพร่แล้ว: 2021-02-22สารบัญ
Gaussian Naive Bayes
Naive Bayes เป็นอัลกอริธึมแมชชีนเลิร์นนิงความน่าจะเป็นที่ใช้สำหรับฟังก์ชันการจำแนกประเภทต่างๆ และอิงตามทฤษฎีบทเบย์ Gaussian Naive Bayes เป็นส่วนขยายของ Bayes ไร้เดียงสา ในขณะที่ฟังก์ชันอื่นๆ ใช้เพื่อประมาณการกระจายข้อมูล การแจกแจงแบบเกาส์เซียนหรือการแจกแจงแบบปกติเป็นวิธีที่ง่ายที่สุดในการใช้งาน เนื่องจากคุณจะต้องคำนวณค่าเฉลี่ยและค่าเบี่ยงเบนมาตรฐานสำหรับข้อมูลการฝึก
อัลกอริทึม Naive Bayes คืออะไร?
Naive Bayes เป็นอัลกอริธึมแมชชีนเลิร์นนิงที่น่าจะใช้ได้ในงานจำแนกหลายประเภท การใช้งานทั่วไปของ Naive Bayes คือการจัดประเภทเอกสาร การกรองสแปม การคาดคะเน และอื่นๆ อัลกอริทึมนี้มีพื้นฐานมาจากการค้นพบของ Thomas Bayes และด้วยเหตุนี้จึงชื่อของมัน
มีการใช้ชื่อ "ไร้เดียงสา" เนื่องจากอัลกอริธึมรวมเอาคุณลักษณะต่างๆ ในรูปแบบที่ไม่ขึ้นกับแต่ละอื่น ๆ การปรับเปลี่ยนมูลค่าของคุณลักษณะหนึ่งจะไม่ส่งผลโดยตรงต่อมูลค่าของคุณลักษณะอื่นๆ ของอัลกอริทึม ข้อได้เปรียบหลักของอัลกอริธึม Naive Bayes คืออัลกอริธึมที่เรียบง่ายแต่ทรงพลัง
มันขึ้นอยู่กับโมเดลความน่าจะเป็นที่สามารถเข้ารหัสอัลกอริธึมได้อย่างง่ายดายและการทำนายทำอย่างรวดเร็วในแบบเรียลไทม์ ดังนั้นอัลกอริธึมนี้จึงเป็นตัวเลือกทั่วไปในการแก้ปัญหาในโลกแห่งความเป็นจริง เนื่องจากสามารถปรับให้ตอบสนองต่อคำขอของผู้ใช้ได้ทันที แต่ก่อนที่เราจะลงลึกใน Naive Bayes และ Gaussian Naive Bayes เราต้องรู้ว่าความน่าจะเป็นแบบมีเงื่อนไขมีความหมายว่าอะไร
อธิบายความน่าจะเป็นแบบมีเงื่อนไข
เราสามารถเข้าใจความน่าจะเป็นแบบมีเงื่อนไขได้ดีขึ้นด้วยตัวอย่าง เมื่อคุณโยนเหรียญ ความน่าจะเป็นที่จะขึ้นนำหรือหางคือ 50% ในทำนองเดียวกัน ความน่าจะเป็นที่จะได้ 4 เมื่อคุณทอยลูกเต๋าด้วยใบหน้าคือ 1/6 หรือ 0.16
ถ้าเราเอาไพ่หนึ่งซอง ความน่าจะเป็นที่จะได้ราชินีด้วยเงื่อนไขว่าเป็นจอบเป็นเท่าไหร่? เนื่องจากเงื่อนไขถูกกำหนดไว้แล้วว่าต้องเป็นจอบ ตัวส่วนหรือชุดการเลือกจึงกลายเป็น 13 ในโพดำมีราชินีเพียงตัวเดียว ดังนั้นความน่าจะเป็นที่จะหยิบไพ่ราชินีโพดำจึงกลายเป็น 1/13 = 0.07

ความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์ A เหตุการณ์ที่กำหนด B หมายถึงความน่าจะเป็นของเหตุการณ์ A ที่เกิดขึ้นเนื่องจากเหตุการณ์ B ได้เกิดขึ้นแล้ว ในทางคณิตศาสตร์ ความน่าจะเป็นแบบมีเงื่อนไขของ A ที่ให้ B สามารถแสดงเป็น P[A|B] = P[A AND B] / P[B]
ให้เราพิจารณาตัวอย่างที่ซับซ้อนเล็กน้อย เข้าเรียนในโรงเรียนที่มีนักเรียนทั้งหมด 100 คน ประชากรนี้สามารถแบ่งเขตได้เป็น 4 หมวดหมู่ - นักเรียน, ครู, ชายและหญิง พิจารณาตารางที่ระบุด้านล่าง:
| หญิง | ชาย | รวม | |
| ครู | 8 | 12 | 20 |
| นักเรียน | 32 | 48 | 80 |
| รวม | 40 | 50 | 100 |
ในที่นี้ ความน่าจะเป็นแบบมีเงื่อนไขที่ผู้อยู่อาศัยในโรงเรียนรายหนึ่งเป็นครูเป็นเท่าใด เมื่อพิจารณาจากเงื่อนไขที่เขาเป็นผู้ชาย
ในการคำนวณ คุณจะต้องกรองประชากรย่อยของชาย 60 คน และเจาะลึกถึงครูชาย 12 คน
ดังนั้น ความน่าจะเป็นแบบมีเงื่อนไขที่คาดหวัง P[Teacher | ชาย] = 12/60 = 0.2
P (ครู | ชาย) = P (ครู ∩ ชาย) / P (ชาย) = 12/60 = 0.2
สามารถแสดงเป็นครู (A) และชาย (B) หารด้วย Male (B) ในทำนองเดียวกัน ค่าความน่าจะเป็นแบบมีเงื่อนไขของ B ที่ให้ A ก็สามารถคำนวณได้เช่นกัน กฎที่เราใช้สำหรับ Naive Bayes สามารถสรุปได้จากสัญลักษณ์ต่อไปนี้:
P (A | B) = P (A ∩ B) / P(B)
P (B | A) = P (A ∩ B) / P(A)
กฎของเบย์
ในกฎ Bayes เราเริ่มจาก P (X | Y) ที่สามารถพบได้จากชุดข้อมูลการฝึกเพื่อค้นหา P (Y | X) เพื่อให้บรรลุสิ่งนี้ สิ่งที่คุณต้องทำคือแทนที่ A และ B ด้วย X และ Y ในสูตรด้านบน สำหรับการสังเกต X จะเป็นตัวแปรที่รู้จักและ Y จะเป็นตัวแปรที่ไม่รู้จัก สำหรับแต่ละแถวของชุดข้อมูล คุณต้องคำนวณความน่าจะเป็นของ Y เนื่องจาก X ได้เกิดขึ้นแล้ว
แต่จะเกิดอะไรขึ้นเมื่อมีมากกว่า 2 หมวดหมู่ใน Y? เราต้องคำนวณความน่าจะเป็นของแต่ละคลาส Y เพื่อหาผู้ชนะ
ตามกฎของ Bayes เราเริ่มจาก P (X | Y) เพื่อค้นหา P (Y | X)
ทราบจากข้อมูลการฝึก: P (X | Y) = P (X ∩ Y) / P(Y)
P (หลักฐาน | ผลลัพธ์)

ไม่ทราบ – คาดการณ์สำหรับข้อมูลการทดสอบ: P (Y | X) = P (X ∩ Y) / P(X)
P (ผลลัพธ์ | หลักฐาน)
กฎเบย์ = P (Y | X) = P (X | Y) * P (Y) / P (X)
The Naive Bayes
กฎ Bayes ให้สูตรสำหรับความน่าจะเป็นของ Y ที่กำหนดเงื่อนไข X แต่ในโลกแห่งความเป็นจริง อาจมีตัวแปร X หลายตัว เมื่อคุณมีคุณสมบัติอิสระ กฎ Bayes สามารถขยายไปยังกฎ Naive Bayes ได้ X เป็นอิสระจากกัน สูตร Naive Bayes มีประสิทธิภาพมากกว่าสูตร Bayes
Gaussian Naive Bayes
จนถึงตอนนี้ เราเห็นว่า X อยู่ในหมวดหมู่ แต่จะคำนวณความน่าจะเป็นอย่างไรเมื่อ X เป็นตัวแปรต่อเนื่อง? หากเราคิดว่า X ตามการแจกแจงเฉพาะ คุณสามารถใช้ฟังก์ชันความหนาแน่นของความน่าจะเป็นของการแจกแจงนั้นเพื่อคำนวณความน่าจะเป็นของความเป็นไปได้
หากเราคิดว่า X ตามหลัง Gaussian หรือการแจกแจงแบบปกติ เราต้องแทนที่ความหนาแน่นของความน่าจะเป็นของการแจกแจงแบบปกติและตั้งชื่อว่า Gaussian Naive Bayes ในการคำนวณสูตรนี้ คุณต้องมีค่าเฉลี่ยและความแปรปรวนของ X
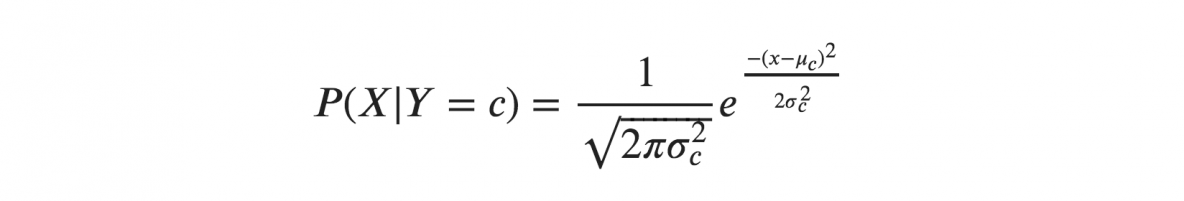
ในสูตรข้างต้น ซิกมาและมิวคือความแปรปรวนและค่าเฉลี่ยของตัวแปรต่อเนื่อง X ที่คำนวณสำหรับคลาส c ที่กำหนดของ Y
ตัวแทนของ Gaussian Naive Bayes
สูตรข้างต้นคำนวณความน่าจะเป็นของค่าอินพุตสำหรับแต่ละคลาสผ่านความถี่ เราสามารถคำนวณค่าเฉลี่ยและค่าเบี่ยงเบนมาตรฐานของ x สำหรับแต่ละคลาส สำหรับการแจกแจงทั้งหมด
ซึ่งหมายความว่าควบคู่ไปกับความน่าจะเป็นของแต่ละคลาส เราต้องเก็บค่าเฉลี่ยและค่าเบี่ยงเบนมาตรฐานสำหรับตัวแปรอินพุตทุกตัวสำหรับคลาส
ค่าเฉลี่ย(x) = 1/n * ผลรวม(x)
โดยที่ n แทนจำนวนอินสแตนซ์และ x คือค่าของตัวแปรอินพุตในข้อมูล
ค่าเบี่ยงเบนมาตรฐาน(x) = sqrt(1/n * sum(xi-mean(x)^2 ))
รากที่สองของค่าเฉลี่ยความแตกต่างของแต่ละ x และค่าเฉลี่ยของ x คำนวณโดยที่ n คือจำนวนอินสแตนซ์ sum() คือฟังก์ชันผลรวม sqrt() คือฟังก์ชันสแควร์รูท และ xi คือค่า x เฉพาะ .

การคาดการณ์ด้วย แบบจำลอง Gaussian Naive Bayes
ฟังก์ชันความหนาแน่นของความน่าจะเป็นแบบเกาส์เซียนสามารถใช้ในการทำนายได้โดยการแทนที่พารามิเตอร์ด้วยค่าอินพุตใหม่ของตัวแปร และด้วยเหตุนี้ ฟังก์ชันเกาส์เซียนจะให้ค่าประมาณความน่าจะเป็นของค่าอินพุตใหม่
Naive Bayes ลักษณนาม
ตัวแยกประเภท Naive Bayes ถือว่าค่าของคุณลักษณะหนึ่งไม่ขึ้นกับค่าของคุณลักษณะอื่นๆ ตัวแยกประเภท Naive Bayes ต้องการข้อมูลการฝึกอบรมเพื่อประเมินพารามิเตอร์ที่จำเป็นสำหรับการจัดประเภท เนื่องจากการออกแบบและการใช้งานที่เรียบง่าย ตัวแยกประเภท Naive Bayes จึงเหมาะกับสถานการณ์จริงมากมาย
บทสรุป
ตัวแยกประเภท Gaussian Naive Bayes เป็นเทคนิคการแยกประเภทที่ง่ายและรวดเร็วซึ่งทำงานได้ดีโดยไม่ต้องใช้ความพยายามมากเกินไปและมีระดับความแม่นยำที่ดี
หากคุณสนใจที่จะเรียนรู้เพิ่มเติมเกี่ยวกับ AI, แมชชีนเลิร์นนิง โปรดดูที่ IIIT-B & upGrad's PG Diploma in Machine Learning & AI ซึ่งออกแบบมาสำหรับมืออาชีพที่ทำงานและมีการฝึกอบรมที่เข้มงวดมากกว่า 450 ชั่วโมง กรณีศึกษาและการมอบหมายมากกว่า 30 รายการ สถานะศิษย์เก่า IIIT-B โครงการหลัก 5 โครงการและความช่วยเหลือด้านงานกับบริษัทชั้นนำ
เรียนรู้ หลักสูตร ML จากมหาวิทยาลัยชั้นนำของโลก รับ Masters, Executive PGP หรือ Advanced Certificate Programs เพื่อติดตามอาชีพของคุณอย่างรวดเร็ว
อัลกอริธึมที่ไร้เดียงสาคืออะไร?
Naive bayes เป็นอัลกอริธึมการเรียนรู้ของเครื่องแบบคลาสสิก มีที่มาในสถิติ naive bayes เป็นอัลกอริธึมที่เรียบง่ายและมีประสิทธิภาพ Naive bayes เป็นตระกูลของตัวแยกประเภทตามการใช้การวิเคราะห์ความน่าจะเป็นแบบมีเงื่อนไข ในการวิเคราะห์นี้ ความน่าจะเป็นแบบมีเงื่อนไขของเหตุการณ์จะคำนวณโดยใช้ความน่าจะเป็นของแต่ละเหตุการณ์ที่ประกอบเป็นเหตุการณ์ ตัวแยกประเภทแบบไร้เดียงสามักพบว่ามีประสิทธิภาพอย่างยิ่งในทางปฏิบัติ โดยเฉพาะอย่างยิ่งเมื่อขนาดของชุดคุณลักษณะมีจำนวนมาก
แอปพลิเคชั่นของอัลกอริธึม naive bayes คืออะไร?
Naive Bayes ใช้ในการจำแนกข้อความ การจัดประเภทเอกสาร และสำหรับการจัดทำดัชนีเอกสาร ในช่องว่างที่ไร้เดียงสา คุณลักษณะที่เป็นไปได้แต่ละอย่างไม่มีการกำหนดน้ำหนักใดๆ ในขั้นตอนก่อนการประมวลผล และจะมีการมอบหมายน้ำหนักในภายหลังระหว่างการฝึกและระยะการจดจำ สมมติฐานพื้นฐานของอัลกอริธึมที่ไร้เดียงสาคือคุณลักษณะที่เป็นอิสระ
อัลกอริทึม Gaussian Naive Bayes คืออะไร?
Gaussian Naive Bayes เป็นอัลกอริธึมการจำแนกประเภทความน่าจะเป็นตามการนำทฤษฎีบทของ Bayes ไปประยุกต์ใช้โดยมีสมมติฐานที่ชัดเจนเกี่ยวกับความเป็นอิสระ ในบริบทของการจำแนกประเภท ความเป็นอิสระหมายถึงแนวคิดที่ว่าการมีอยู่ของค่าหนึ่งของจุดสนใจไม่ส่งผลต่อการมีอยู่ของอีกค่าหนึ่ง (ต่างจากความเป็นอิสระในทฤษฎีความน่าจะเป็น) ไร้เดียงสาหมายถึงการใช้สมมติฐานที่ว่าคุณสมบัติของวัตถุเป็นอิสระจากกัน ในบริบทของแมชชีนเลิร์นนิง ตัวแยกประเภท Bayes ที่ไร้เดียงสาเป็นที่ทราบกันดีอยู่แล้วว่าสามารถแสดงออกอย่างชัดเจน ปรับขนาดได้ และถูกต้องตามสมควร แต่ประสิทธิภาพจะลดลงอย่างรวดเร็วตามการเติบโตของชุดการฝึก คุณลักษณะหลายประการมีส่วนสนับสนุนความสำเร็จของตัวแยกประเภท Bayes ที่ไร้เดียงสา ที่โดดเด่นที่สุดก็คือ พวกมันไม่ต้องการการปรับแต่งพารามิเตอร์ของแบบจำลองการจัดหมวดหมู่ใดๆ พวกมันปรับขนาดได้ดีกับขนาดของชุดข้อมูลการฝึก และสามารถจัดการกับคุณสมบัติที่ต่อเนื่องกันได้อย่างง่ายดาย
