อนุพันธ์กฎลูกโซ่ในการเรียนรู้ของเครื่อง : อธิบาย

แมชชีนเลิร์นนิงได้พัฒนาจนกลายเป็นหนึ่งในสาขาที่มีการพูดถึงและค้นคว้ามากที่สุดในปีปัจจุบัน และด้วยเหตุผลที่ดีทั้งหมด มีการค้นพบโมเดลและแอปพลิเคชันใหม่ๆ ของแมชชีนเลิร์นนิงทุกวัน และนักวิจัยทั่วโลกก็กำลังทำงานเพื่อมุ่งสู่สิ่งที่ยิ่งใหญ่ต่อไป

เป็นผลให้มีความสนใจเพิ่มขึ้นในผู้เชี่ยวชาญจากภูมิหลังที่หลากหลายเพื่อเปลี่ยนไปใช้การเรียนรู้ของเครื่องและเป็นส่วนหนึ่งของการปฏิวัติอย่างต่อเนื่องนี้ หากคุณเป็นคนหนึ่งที่คลั่งไคล้แมชชีนเลิร์นนิงที่ต้องการเริ่มก้าวแรก สมมติว่ามันเริ่มต้นจากการทำความเข้าใจพื้นฐานของคณิตศาสตร์และสถิติก่อนสิ่งอื่นใด

หัวข้อสำคัญอย่างหนึ่งในวิชาคณิตศาสตร์ที่มีความเกี่ยวข้องสูงกับการเรียนรู้ของเครื่องคืออนุพันธ์ จากความเข้าใจพื้นฐานของแคลคูลัส คุณจะจำได้ว่าอนุพันธ์ของฟังก์ชันใดๆ คือ อัตราการเปลี่ยนแปลงในทันทีของฟังก์ชันนั้น ในบล็อกนี้ เราจะเจาะลึกเกี่ยวกับอนุพันธ์และสำรวจกฎลูกโซ่ เราจะเห็นว่าผลลัพธ์ของฟังก์ชันเฉพาะเปลี่ยนแปลงไปอย่างไรเมื่อเราเปลี่ยนตัวแปรอิสระบางตัวในสมการ ด้วยความรู้เกี่ยวกับอนุพันธ์ของกฎลูกโซ่ คุณจะสามารถทำงานเพื่อสร้างความแตกต่างให้กับฟังก์ชันที่ซับซ้อนมากขึ้น ซึ่งแน่นอนว่าจะต้องพบในการเรียนรู้ของเครื่อง

รับ ใบรับรองการเรียนรู้ของเครื่อง ออนไลน์จากมหาวิทยาลัยชั้นนำของโลก – ปริญญาโท โปรแกรม Executive Post Graduate และหลักสูตรประกาศนียบัตรขั้นสูงใน ML & AI เพื่อติดตามอาชีพของคุณอย่างรวดเร็ว

การทำความเข้าใจอนุพันธ์ของกฎลูกโซ่

กฎลูกโซ่เป็นสูตรทางคณิตศาสตร์ที่ช่วยให้คุณคำนวณอนุพันธ์ของฟังก์ชันคอมโพสิตได้ ฟังก์ชันคอมโพสิตคือฟังก์ชันที่ประกอบด้วยฟังก์ชันตั้งแต่สองฟังก์ชันขึ้นไป ดังนั้น ถ้า f และ g เป็นฟังก์ชันสองฟังก์ชัน ดังนั้นกฎลูกโซ่จะช่วยเราหาอนุพันธ์ของฟังก์ชันคอมโพสิต เช่น หมอก หรือ go f

เมื่อพิจารณาถึง หมอก ฟังก์ชันคอมโพสิต อนุพันธ์ของกฎลูกโซ่จะมีลักษณะดังนี้:

กฎข้างต้นสามารถเขียนได้ดังนี้:

โดยที่ฟังก์ชัน F คือองค์ประกอบของ f และ g ในรูปของ f(g(x))

ทีนี้ สมมติว่าเรามีตัวแปรสามตัว โดยที่ตัวแปรที่สาม (z) ขึ้นอยู่กับตัวแปรที่สอง (y) ซึ่งจะขึ้นอยู่กับตัวแปรตัวแรก (x) ในกรณีนั้น อนุพันธ์ของกฎลูกโซ่จะมีลักษณะดังนี้:

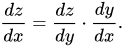ในแง่ของการเรียนรู้เชิงลึก นี่เป็นสูตรที่ใช้เป็นประจำในการแก้ปัญหาการแพร่กระจายกลับหลัง เนื่องจากเรากล่าวว่า z ขึ้นอยู่กับ y และ y บน x เราจึงสามารถเขียน z = f(y) และ y = g(x) ได้ การแทนที่นี้จะแก้ไขสมการเชิงอนุพันธ์ในลักษณะต่อไปนี้:

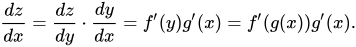ทีนี้ มาดูตัวอย่างอนุพันธ์กฎลูกโซ่เพื่อทำความเข้าใจคณิตศาสตร์เบื้องหลังกันดีกว่า

ตัวอย่างและการประยุกต์ใช้อนุพันธ์ของกฎลูกโซ่

ให้เรายกตัวอย่างที่รู้จักกันดีจาก Wikipedia เพื่อทำความเข้าใจอนุพันธ์ของกฎลูกโซ่ในลักษณะที่ดีขึ้น สมมติว่าคุณกำลังตกลงมาจากฟากฟ้า ความกดอากาศที่คุณพบในช่วงฤดูใบไม้ร่วงจะเปลี่ยนแปลงตลอดเวลา นี่คือกราฟที่แสดงการเปลี่ยนแปลงของความกดอากาศในระดับระดับความสูง:

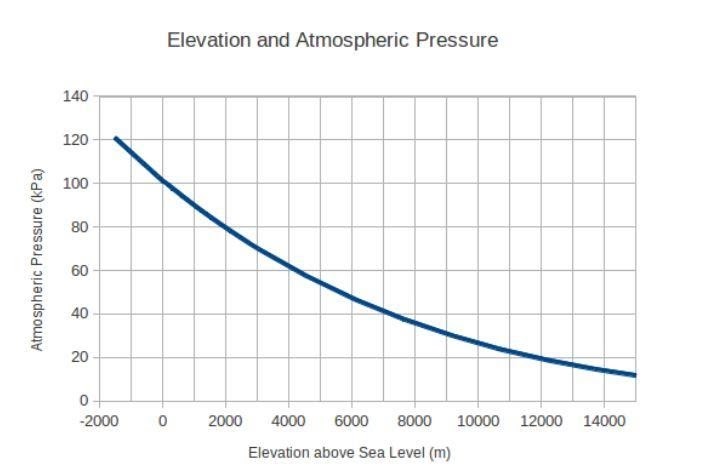
สมมติว่าคุณเริ่มล้มที่ความสูง 4000 เมตรเหนือระดับน้ำทะเล ในขั้นต้น ความเร็วของคุณเป็นศูนย์ และความเร่งคือ 9.8 เมตรต่อวินาทียกกำลังสองเนื่องจากแรงโน้มถ่วง

ตอนนี้ มาเปรียบเทียบสถานการณ์นี้กับวิธีกฎลูกโซ่ก่อนหน้านี้ ในตัวอย่างนี้ เราจะใช้ตัวแปร 't' แทนค่า x

จากนั้น ตัวแปร y = g(t) ซึ่งบอกระยะทางที่เดินทางตั้งแต่ต้นฤดูใบไม้ร่วง สามารถกำหนดได้ดังนี้

ก.(เสื้อ) = 0.5*9.8t^2

และความสูงจากระดับน้ำทะเลสามารถกำหนดได้ด้วยตัวแปร 'h' ซึ่งจะเท่ากับ 400-g(t)

สมมติว่า ตามแบบจำลอง เราสามารถเขียนฟังก์ชันของความดันบรรยากาศที่ความสูงใดๆ h ได้ดังนี้:

f(h) = 101325 e−0.0001h

ตอนนี้คุณสามารถแยกความแตกต่างระหว่างสมการทั้งสองตามตัวแปรตามเพื่อให้ได้ผลลัพธ์ต่อไปนี้:

g′(t) = −9.8t,

ที่นี่ g'(t) บอกค่าความเร็วของคุณเมื่อใดก็ได้ t

f′(h) = −10.1325e−0.0001h

โดยที่ f′(h) คืออัตราการเปลี่ยนแปลงของความดันบรรยากาศเทียบกับความสูง h ตอนนี้ คำถามคือเราสามารถรวมสมการทั้งสองนี้และรับอัตราการเปลี่ยนแปลงของแรงดัน atm ในเวลานี้ได้หรือไม่? ลองดูการใช้กฎลูกโซ่:

สมการสุดท้ายที่เราได้รับทำให้เรามีอัตราการเปลี่ยนแปลงของความดันบรรยากาศที่สัมพันธ์กับเวลาที่ผ่านไปตั้งแต่ฤดูใบไม้ร่วง ในแง่ของแมชชีนเลิร์นนิง โครงข่ายประสาทจำเป็นต้องมีการอัปเดตน้ำหนักอยู่เสมอเกี่ยวกับข้อผิดพลาดในการทำนายของเซลล์ประสาท กฎลูกโซ่ช่วยปรับน้ำหนักเหล่านี้และทำให้โมเดลการเรียนรู้ของเครื่องใกล้กับเอาต์พุตที่ถูกต้องมากขึ้น

บทสรุป

อย่างที่คุณเห็น กฎลูกโซ่มีประโยชน์สำหรับหลายวัตถุประสงค์ โดยเฉพาะอย่างยิ่งเมื่อพูดถึงแมชชีนเลิร์นนิงหรือการเรียนรู้เชิงลึก กฎลูกโซ่พบว่ามีประโยชน์อย่างมากในการปรับปรุงน้ำหนักของเซลล์ประสาทและปรับปรุงประสิทธิภาพโดยรวมของแบบจำลอง

เมื่อคุณได้ทราบถึงพื้นฐานของกฎลูกโซ่แล้ว ให้ลองทำปัญหาสองสามข้อด้วยตัวเอง ค้นหาฟังก์ชันประกอบสองสามอย่างแล้วลองหาอนุพันธ์ของพวกมัน ยิ่งคุณฝึกฝนมาก แนวคิดของคุณก็จะยิ่งชัดเจนขึ้น และการฝึกโมเดลการเรียนรู้ของเครื่องก็จะยิ่งง่ายขึ้น! ที่กล่าวว่าหากคุณเป็นผู้ที่ชื่นชอบแมชชีนเลิร์นนิงแต่พยายามดิ้นรนเพื่อก้าวแรกในสาขานี้ upGrad ช่วยคุณได้!

โปรแกรม Executive PG ของเรา ในการเรียนรู้ของเครื่องและ AI นำเสนอร่วมกับ IIIT-Bangalore และให้คุณเลือกความเชี่ยวชาญเฉพาะทางที่เกี่ยวข้องกับอุตสาหกรรมหกรายการ หลักสูตรนี้เริ่มต้นจากระดับพื้นดินและนำคุณไปสู่จุดสูงสุดพร้อมกับการสนับสนุนแบบตัวต่อตัวจากผู้เชี่ยวชาญในอุตสาหกรรม กลุ่มนักศึกษาที่เข้มแข็ง และการสนับสนุนด้านอาชีพแบบ 360 องศา