Binary Tree กับ Binary Search Tree: ความแตกต่างระหว่าง Binary Tree และ Binary Search Tree
เผยแพร่แล้ว: 2021-01-21สารบัญ
บทนำ
การเรียงลำดับเป็นกระบวนการของการจัดเรียงข้อมูลอย่างเป็นระบบเพื่อให้สามารถวิเคราะห์ได้อย่างมีประสิทธิภาพมากขึ้น กระบวนการระบุเรกคอร์ดเฉพาะเรียกว่าการค้นหา หากข้อมูลถูกจัดเรียงอย่างเหมาะสมในลำดับเฉพาะ การค้นหาจะกลายเป็นงานที่ง่ายและมีประสิทธิภาพ บทความนี้กล่าวถึงโครงสร้างข้อมูลที่ไม่เชิงเส้นที่สำคัญที่สุดอย่างหนึ่ง เช่น ต้นไม้
โดยหลักแล้ว ต้นไม้จะใช้เพื่อแสดงข้อมูลโดยแสดงความสัมพันธ์แบบลำดับชั้นระหว่างองค์ประกอบต่างๆ ตัวอย่างเช่น สารบัญ แผนภูมิต้นไม้ครอบครัว ในทางเทคนิค ต้นไม้อาจถูกกำหนดเป็นชุดจำกัด 'T' ของโหนดอย่างน้อยหนึ่งโหนดเพื่อให้โหนดถูกกำหนดให้เป็นรากของต้นไม้และโหนดอื่น ๆ จะถูกแบ่งออกเป็น n>=0 ชุดที่ไม่ปะติดปะต่อกัน T1, T2, T3, ท4 …. Tn และถูกเรียกว่าเป็นทรีย่อยหรือลูกของโหนดรูทนั้น
ต้นไม้ไบนารีคืออะไร?
ต้นไม้ไบนารีเป็นโครงสร้างข้อมูลที่ไม่เชิงเส้นซึ่งโหนดสามารถมีได้ 0, 1 หรือ 2 โหนด แต่ละโหนดในไบนารีทรีเรียกว่าโหนดหลักหรือโหนดย่อย โหนดบนสุดของไบนารีทรีเรียกว่าโหนดรูท โหนดหลักแต่ละโหนดสามารถมีโหนดย่อยได้ไม่เกิน 2 โหนด ซึ่งเป็นโหนดย่อยด้านซ้ายและโหนดย่อยด้านขวา
โหนดในไบนารีทรีมีสามฟิลด์:
- องค์ประกอบข้อมูล – จัดเก็บค่าข้อมูลที่จะจัดเก็บโดยโหนด
- ตัวชี้ไปที่ลูกด้านซ้าย – เก็บข้อมูลอ้างอิง (หรือที่อยู่) ไปยังโหนดลูกด้านซ้าย
- ตัวชี้ไปยังชายด์ที่ถูกต้อง – เก็บข้อมูลอ้างอิงไปยังโหนดชายด์ด้านขวา
ด้วยวิธีนี้ หลายโหนดจะรวมกันเพื่อสร้าง Binary Tree
ต้นไม้ไบนารีสามารถแสดงเป็น:
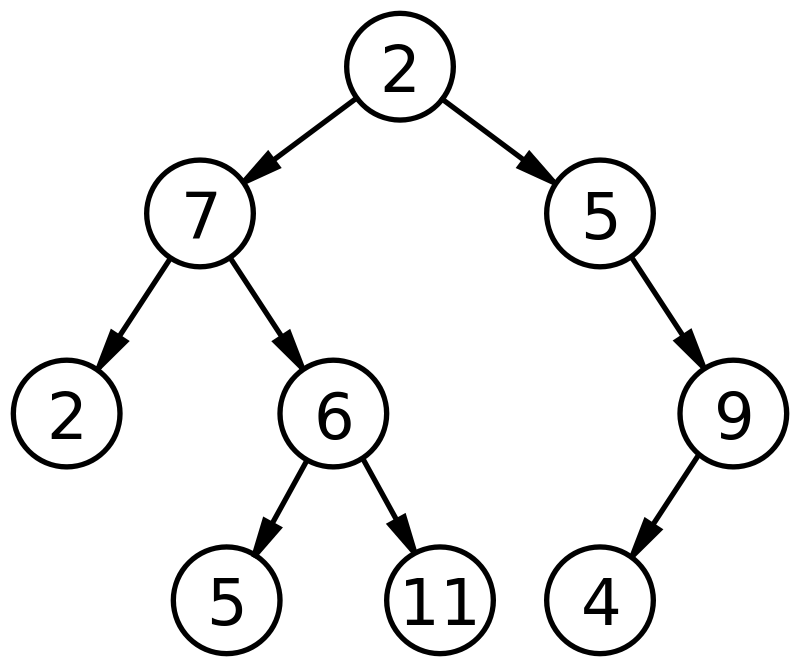
แหล่งที่มา
จากรูปด้านบน โหนดรูท 2 มีลูกสองคน (หรือโหนดย่อย) 7 และ 5. 7 เรียกว่าโหนดลูกด้านซ้ายและ 5 เรียกว่าโหนดลูกด้านขวา ด้วยวิธีนี้ โหนดย่อยแต่ละโหนดจะทำหน้าที่เป็นโหนดหลักสำหรับโหนดอื่นๆ หลายโหนด และร่วมกันเป็นตัวแทนของทรีไบนารี
ตรวจสอบ: ประเภทของไบนารีทรี
คำศัพท์ที่ใช้ใน Binary Tree
โหนด : การแสดงพื้นฐานของจุดสิ้นสุดในต้นไม้
Root Node : โหนดบนสุดของไบนารีทรี
โหนด หลัก : หากโหนดเชื่อมต่อกับโหนดอื่นผ่านขอบ จะเรียกว่าโหนดหลัก ในไบนารีทรี โหนดหลักสามารถมีโหนดย่อยได้สูงสุด 2 โหนด
โหนด ย่อย : หากโหนดมีรุ่นก่อน จะเรียกว่าโหนดย่อย
Leaf Node : โหนดที่ไม่มีโหนดย่อยเรียกว่าโหนดปลายสุด
ความลึกของโหนด : คือระยะห่างจากโหนดรูทไปยังโหนดนั้นที่ต้องการวัดความลึก
ความสูงของต้นไม้ : ระยะทางที่ยาวที่สุดจากโหนดรากถึงโหนดใบ
นี่เป็นคำศัพท์พื้นฐานบางประการของไบนารีทรี ด้วยความเข้าใจพื้นฐานเกี่ยวกับ Binary Tree ให้เราก้าวไปสู่ความก้าวหน้าของ Binary Tree ที่รู้จักกันในชื่อ Binary Search Tree
อ่านเพิ่มเติม: อัลกอริทึมการค้นหาแบบไบนารี: ฟังก์ชัน ประโยชน์ เวลา & ความซับซ้อนของพื้นที่
Binary Search Tree คืออะไร
ตามชื่อที่แนะนำ Binary Search Tree หรือ BST เป็นต้นไม้ที่ใช้ในการเรียงลำดับ ดึงข้อมูล และค้นหาข้อมูล นอกจากนี้ยังเป็นประเภทของโครงสร้างข้อมูลที่ไม่เป็นเชิงเส้นซึ่งโหนดถูกจัดเรียงตามลำดับเฉพาะ ดังนั้นจึงเรียกอีกอย่างว่า " Ordered Binary Tree " มีคุณสมบัติดังต่อไปนี้:
- ทรีย่อยด้านซ้ายของโหนดมีโหนดที่น้อยกว่าคีย์ของโหนดนั้นเท่านั้น
- แผนผังย่อยด้านขวาของโหนดมีโหนดที่มากกว่าคีย์ของโหนดนั้นเท่านั้น
- แต่ละโหนดมีคีย์ที่แตกต่างกันและไม่อนุญาตให้ทำซ้ำในแผนผังการค้นหาแบบไบนารี
- ทรีย่อยด้านซ้ายและขวาจะต้องเป็นแผนผังการค้นหาแบบไบนารีด้วย
ให้เราเห็นภาพแนวคิดนี้เพื่อทำความเข้าใจต้นไม้การค้นหาไบนารีอย่างชัดเจน
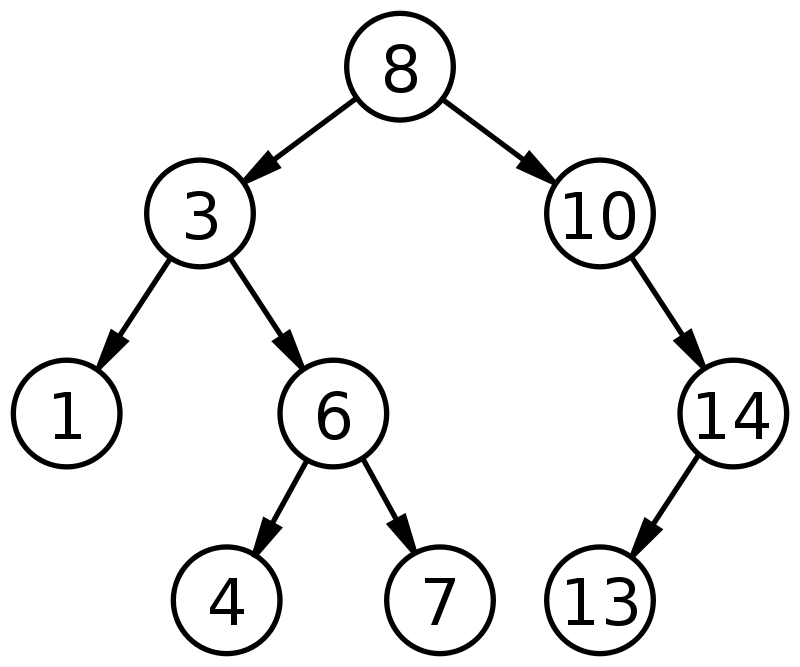
แหล่งที่มา
ในรูปด้านบน เราจะเห็นว่าค่าของโหนดรูทคือ 8 เมื่อพิจารณาอย่างละเอียดแล้ว จะพบว่าค่าทั้งหมดในทรีย่อยทางซ้ายนั้นน้อยกว่าค่าของโหนดรูท และค่าทั้งหมดในทรีย่อยทางขวาจะมี ค่าที่มากกว่าโหนดรูท นอกจากนี้ ยังสังเกตว่าแต่ละค่าในแผนผังการค้นหาแบบไบนารีนั้นไม่ซ้ำกันและไม่มีการซ้ำกัน ดังนั้นคุณสมบัติของ Binary Search Tree ที่ระบุไว้ข้างต้นจึงได้รับการตรวจสอบ
ในอีกตัวอย่างหนึ่ง เราเห็นว่าแม้ว่าทรีย่อยด้านซ้ายและขวาเป็นทรีการค้นหาแบบไบนารีที่มีค่าที่ไม่ซ้ำกันทั่วทั้งทรี ค่าที่โหนดปลายสุดในทรีย่อยด้านซ้ายคือ 12 ซึ่งมากกว่าค่าโหนดรูทซึ่งก็คือ 12 ดังนั้น ค่านี้จึงไม่เป็นไปตามคุณสมบัติของ BST และด้วยเหตุนี้จึงไม่ใช่ทรีการค้นหาแบบไบนารี
การดำเนินการค้นหาใน BST –
พิจารณา Binary Search Tree ด้วยค่าที่ระบุด้านล่าง ให้เราเข้าใจวิธีการดำเนินการค้นหาเพื่อรับ 9 จาก Binary Search Tree

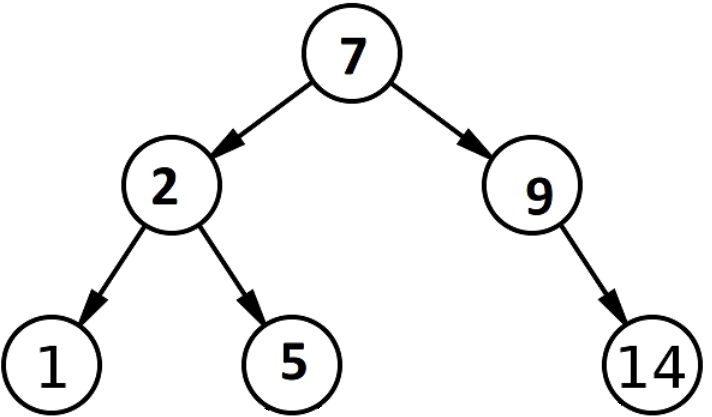
แหล่งที่มา
ในการดำเนินการค้นหาแบบไบนารี ขั้นแรกเราจะจัดเรียงจำนวนเต็มทั้งหมดในอาร์เรย์ที่จัดเรียง นี่เรียกว่าเป็นพื้นที่ค้นหา พื้นที่การค้นหานี้จะประกอบด้วยตัวชี้สองตัว เรียกว่าตัวชี้เริ่มต้นและจุดสิ้นสุด อาร์เรย์ของ Binary Search Tree ที่ระบุข้างต้นจะแสดงเป็น:
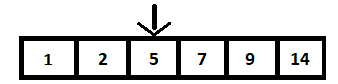
ขั้นตอนแรกคือการคำนวณค่ากลางของอาร์เรย์และเปรียบเทียบกับค่าที่จะค้นหา เช่น 9 ในกรณีของเรา ทำได้โดยการคำนวณ n/2 โดยที่ n คือจำนวนองค์ประกอบทั้งหมดในอาร์เรย์ (BST) และมีค่าเท่ากับ 6 ดังนั้น องค์ประกอบที่ 3 จึง เป็นองค์ประกอบตรงกลางซึ่งเท่ากับ 5
เมื่อเปรียบเทียบองค์ประกอบตรงกลางกับ 9 และเนื่องจากไม่เท่ากัน (มากกว่า) การค้นหาจะดำเนินการในอาร์เรย์ที่ถูกต้อง ด้วยวิธีนี้ การดำเนินการค้นหาจะลดลงเหลือครึ่งหนึ่ง ดังที่แสดงด้านล่าง:
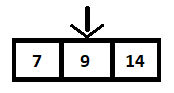
ในขั้นตอนต่อไป เราจะคำนวณองค์ประกอบตรงกลางและพบว่ามีค่าเท่ากับ 9 ซึ่งตรงกับองค์ประกอบที่เราจะค้นหา
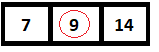
Binary Tree กับ Binary Search Tree –
ตอนนี้เรามีความเข้าใจพื้นฐานเกี่ยวกับทั้ง Binary Tree และ Binary Search Tree แล้ว ให้เราสรุปความแตกต่างระหว่างทั้งสองอย่างรวดเร็ว
| พื้นฐานสำหรับการเปรียบเทียบ | ต้นไม้ไบนารี | แผนผังการค้นหาไบนารี |
| คำนิยาม | Binary Tree เป็นโครงสร้างข้อมูลที่ไม่เป็นเชิงเส้น ซึ่งโหนดสามารถมีได้ 0, 1 หรือ 2 โหนด แต่ละโหนดประกอบด้วยตัวชี้ด้านซ้าย ตัวชี้ด้านขวา และองค์ประกอบข้อมูล | Binary Search Tree เป็นไบนารีทรีที่มีการจัดระเบียบซึ่งมีโครงสร้างเป็นโหนดของโหนด ทรีย่อยแต่ละอันต้องมีโครงสร้างเฉพาะนั้นด้วย |
| โครงสร้าง | ไม่มีโครงสร้างองค์กรที่จำเป็นของโหนดในแผนผัง | ค่าของทรีย่อยด้านซ้ายของโหนดเฉพาะควรน้อยกว่าโหนดนั้น และค่าทรีย่อยทางขวาควรมากกว่า |
| ดำเนินการแล้ว | การดำเนินการที่สามารถทำได้คือ การลบ การแทรก และการข้ามผ่าน | เนื่องจากเป็นไบนารีทรีที่จัดเรียง จึงใช้สำหรับการค้นหา การแทรก และการลบไบนารีที่รวดเร็วและมีประสิทธิภาพ |
| ประเภท | มีหลายประเภท สิ่งที่พบบ่อยที่สุดคือ Complete Binary Tree, Full Binary Tree, Extended Binary Tree | ต้นไม้ที่ได้รับความนิยมมากที่สุด ได้แก่ AVL Trees, Splay Trees, Tango Trees, T-Trees |
บทสรุป
ดังนั้น เราอนุมานได้ว่าแม้ว่าทั้ง Binary Tree และ Binary Search Tree จะมีโครงสร้างแบบลำดับชั้นร่วมกับคอลเลกชั่นของโหนด แต่ก็มีความแตกต่างกันหลายประการในแอปพลิเคชัน Binary Tree เป็นโครงสร้างพื้นฐานที่มีกฎง่ายๆ ว่าไม่มีพาเรนต์ใดต้องมีลูกมากกว่า 2 ลูก ในขณะที่ Binary Search Tree เป็นตัวแปรของไบนารีทรีตามลำดับเฉพาะที่ควรจัดระเบียบโหนด
หากคุณอยากเรียนรู้เกี่ยวกับ Binary tree กับ Binary search tree โปรดดูที่ IIIT-B & upGrad's PG Diploma in Data Science ซึ่งสร้างขึ้นสำหรับมืออาชีพที่ทำงานและเสนอกรณีศึกษาและโครงการมากกว่า 10+ เวิร์กช็อปเชิงปฏิบัติ การให้คำปรึกษากับอุตสาหกรรม ผู้เชี่ยวชาญ ตัวต่อตัวกับที่ปรึกษาในอุตสาหกรรม การเรียนรู้มากกว่า 400 ชั่วโมงและความช่วยเหลือด้านงานกับบริษัทชั้นนำ
เรียนรู้ หลักสูตรวิทยาศาสตร์ข้อมูล ออนไลน์จากมหาวิทยาลัยชั้นนำของโลก รับโปรแกรม PG สำหรับผู้บริหาร โปรแกรมประกาศนียบัตรขั้นสูง หรือโปรแกรมปริญญาโท เพื่อติดตามอาชีพของคุณอย่างรวดเร็ว
เราจะสำรวจ Binary Search Tree ได้อย่างไร?
ต่างจากโครงสร้างข้อมูลเชิงเส้นอย่างอาร์เรย์ รายการที่เชื่อมโยง สแต็ค และคิว ซึ่งเราสามารถสำรวจโครงสร้างข้อมูลด้วยวิธีเดียวเท่านั้น Binary Search Tree ให้อิสระแก่เราในการข้ามผ่านได้หลายวิธี การข้ามผ่านต้นไม้ที่ได้รับความนิยมมากที่สุดมีดังนี้: ในการข้ามผ่านแบบไม่เรียงลำดับ เราจะสำรวจโหนดทางซ้ายของต้นไม้ก่อน จากนั้นจึงไปที่โหนดรูทของต้นไม้ และสุดท้ายไปที่โหนดทางขวาของต้นไม้ เราปฏิบัติตามแนวทางเดียวกันในทรีย่อยทั้งหมดเช่นกัน ในการข้ามผ่านของการสั่งซื้อล่วงหน้า ก่อนอื่น เราจะสำรวจโหนดรูทของต้นไม้ จากนั้นจึงไปที่โหนดทางซ้ายและขวาตามลำดับ เราปฏิบัติตามแนวทางเดียวกันในทรีย่อยทั้งหมดเช่นกัน ในการข้ามผ่านคำสั่งภายหลัง เราจะสำรวจโหนดทางซ้ายและขวาของต้นไม้ตามลำดับ และสุดท้ายไปยังโหนดรากของต้นไม้ เราปฏิบัติตามแนวทางเดียวกันในทรีย่อยทั้งหมดเช่นกัน
ข้อดีและข้อเสียของ BST คืออะไร?
ต่อไปนี้เป็นข้อดีและข้อเสียของ Binary Search Tree ข้อดีคือ - การดำเนินการต่างๆ เช่น การแทรก การลบ และการค้นหาสามารถทำได้ในเวลา O(log n) โดยที่ n คือจำนวนโหนด องค์ประกอบทั้งหมดใน BST ได้รับการจัดเรียงเพื่อให้เราสามารถสำรวจผ่าน BST ได้อย่างง่ายดายโดยใช้การข้ามผ่านแบบไม่เรียงลำดับ BST สามารถใช้ออกแบบตัวจัดสรรหน่วยความจำได้อย่างมีประสิทธิภาพ เพื่อเพิ่มความเร็วในกระบวนการค้นหาของบล็อกหน่วยความจำ ข้อเสียที่ใหญ่ที่สุดของ Binary Search Tree คือ เราต้องใช้ BST ที่สมดุลเสมอ เช่น AVL และ Red-Black Tree เพราะหากเราไม่ใช้ BST ที่สมดุล การดำเนินการของทรีของเราจะไม่ถูกดำเนินการในเวลาลอการิทึม
แยกความแตกต่างระหว่างต้นไม้ไบนารีแบบเต็มและต้นไม้ไบนารีที่สมบูรณ์
ต้นไม้ไบนารีแบบเต็มคือไบนารีทรีที่โหนดทั้งหมดมีโหนดย่อยระหว่าง 0 ถึง 2 กล่าวอีกนัยหนึ่ง ต้นไม้ไบนารีที่โหนดทั้งหมดมีโหนดย่อยอย่างน้อย 2 โหนด ยกเว้นโหนดปลายสุดเรียกว่าต้นไม้ไบนารีแบบเต็ม ในทางกลับกัน ต้นไม้ไบนารีที่สมบูรณ์คือไบนารีทรีที่ทุกโหนดถูกเติมอย่างสมบูรณ์ (โหนดลูกสองโหนด) และโหนดปลายสุดจะตั้งอยู่ซ้ายสุด
