สถิติและแบบจำลองเบย์: อธิบาย

เทคนิค Bayesian เป็นแนวทางในสถิติที่ใช้ในการวิเคราะห์ข้อมูลและการประมาณค่าพารามิเตอร์ วิธีนี้ใช้ทฤษฎีบทเบย์

สถิติแบบเบย์เป็นไปตามหลักการเฉพาะซึ่งจะช่วยกำหนดการกระจายความน่าจะเป็นร่วมกันสำหรับพารามิเตอร์ที่สังเกตและไม่ได้สังเกตโดยใช้แบบจำลองทางสถิติ ความรู้ด้านสถิติมีความสำคัญต่อการจัดการปัญหาการวิเคราะห์ในสถานการณ์นี้

นับตั้งแต่การนำทฤษฎีบทเบย์ส์มาใช้ในปี 1770 โดยโธมัส เบย์ส์ มันยังคงเป็นเครื่องมือที่ขาดไม่ได้ในด้านสถิติ โมเดล Bayesian เป็นการแทนที่แบบคลาสสิกสำหรับโมเดลที่ใช้บ่อย เนื่องจากนวัตกรรมล่าสุดในสถิติได้ช่วยละเมิดเหตุการณ์สำคัญในหลากหลายอุตสาหกรรม รวมถึงการวิจัยทางการแพทย์ การทำความเข้าใจการค้นหาเว็บ และการประมวลผลภาษาธรรมชาติ (การประมวลผลภาษาธรรมชาติ)

ตัวอย่างเช่น โรคอัลไซเมอร์เป็นโรคที่ทราบกันว่ามีความเสี่ยงเพิ่มขึ้นเมื่ออายุมากขึ้น อย่างไรก็ตาม ด้วยความช่วยเหลือของทฤษฎีบทเบย์ แพทย์สามารถประเมินความน่าจะเป็นของคนที่จะเป็นโรคอัลไซเมอร์ได้ในอนาคต นอกจากนี้ยังใช้กับโรคมะเร็งและการเจ็บป่วยที่เกี่ยวข้องกับอายุอื่น ๆ ที่บุคคลนั้นเสี่ยงต่อชีวิตของเขาในปีต่อ ๆ ไป

สถิติที่ใช้บ่อยกับสถิติแบบเบย์

สถิติที่ใช้บ่อยกับสถิติแบบเบย์เป็นหัวข้อของการโต้เถียงและฝันร้ายสำหรับผู้เริ่มต้นมาโดยตลอด ซึ่งทั้งคู่ต่างก็มีปัญหาในการเลือกระหว่างทั้งสอง ในช่วงต้นศตวรรษที่ 20 สถิติแบบเบย์ได้รับส่วนแบ่งของปัญหาความไม่ไว้วางใจและการยอมรับ อย่างไรก็ตาม เมื่อเวลาผ่านไป ผู้คนต่างตระหนักถึงความเหมาะสมของแบบจำลองเบย์เซียนและวิธีแก้ไขปัญหาที่แม่นยำ

ต่อไปนี้คือการพิจารณาสถิติที่ใช้บ่อยและความซับซ้อนที่เกี่ยวข้อง:

สถิติที่ใช้บ่อย

เป็นวิธีการอนุมานที่ใช้กันอย่างแพร่หลายในโลกของสถิติ โดยจะวิเคราะห์ว่าเหตุการณ์ (ที่กล่าวถึงเป็นสมมติฐาน) เกิดขึ้นหรือไม่ นอกจากนี้ยังประมาณการความน่าจะเป็นของเหตุการณ์ที่เกิดขึ้นระหว่างช่วงการทดสอบ การทดลองซ้ำจนกว่าจะได้ผลลัพธ์ที่ต้องการ

ตัวอย่างการแจกแจงของพวกมันมีขนาดจริง และการทดลองนั้นซ้ำแล้วซ้ำเล่าเป็นอนันต์ตามทฤษฎี ต่อไปนี้คือตัวอย่างที่แสดงความถี่ในการใช้สถิติเพื่อศึกษาการโยนเหรียญ

• ความเป็นไปได้ในการโยนเหรียญหนึ่งครั้งคือ 0.5 (1/2)
• จำนวนหัวหมายถึงจำนวนลูกค้าเป้าหมายที่แท้จริงที่ได้รับ
• ความแตกต่างระหว่างจำนวนหัวจริงกับจำนวนหัวที่คาดหวังจะเพิ่มขึ้นตามจำนวนครั้งของการโยนที่เพิ่มขึ้น

ดังนั้น ผลลัพธ์จะขึ้นอยู่กับจำนวนครั้งที่ทำการทดสอบซ้ำ มันเป็นข้อเสียเปรียบที่สำคัญของสถิติที่ใช้บ่อย

ข้อบกพร่องอื่น ๆ ที่เกี่ยวข้องกับเทคนิคการออกแบบและการตีความปรากฏชัดในศตวรรษที่ 20 เมื่อการใช้สถิติบ่อยครั้งกับแบบจำลองเชิงตัวเลขอยู่ที่จุดสูงสุด

ข้อจำกัดของสถิติที่ใช้บ่อย

ข้อบกพร่องที่สำคัญสามประการของสถิติที่ใช้บ่อยมีการระบุไว้ด้านล่าง:

1. ค่า p ตัวแปร

ค่าของ p ที่วัดสำหรับตัวอย่างที่มีขนาดคงที่ในการทดสอบโดยมีการเปลี่ยนแปลงจุดปลายที่กำหนด โดยมีการเปลี่ยนแปลงใดๆ ในจุดสิ้นสุดและขนาดตัวอย่าง ส่งผลให้ค่า p สองค่าสำหรับข้อมูลเดียวที่ไม่ถูกต้อง

2. ช่วงความเชื่อมั่นที่ไม่สอดคล้องกัน

CI (Confidence Interval) ขึ้นอยู่กับขนาดกลุ่มตัวอย่างเท่านั้น มันทำให้ศักยภาพในการหยุดไม่เกี่ยวข้อง

3. ค่าประมาณของ CI

ช่วงความเชื่อมั่นไม่ใช่การแจกแจงความน่าจะเป็น และค่าสำหรับพารามิเตอร์เป็นเพียงค่าประมาณเท่านั้น ไม่ใช่ค่าจริง

เหตุผลสามประการข้างต้นทำให้เกิดแนวทางแบบเบย์ซึ่งนำความน่าจะเป็นมาใช้กับปัญหาทางสถิติ

กำเนิดของสถิติเบย์

สาธุคุณโธมัส เบย์ส์ ได้เสนอแนวทางแบบเบย์เซียนในด้านสถิติเป็นครั้งแรกในเรียงความของเขาที่เขียนขึ้นในปี ค.ศ. 1763 แนวทางนี้เผยแพร่โดยริชาร์ด ไพรซ์เป็นกลยุทธ์ในความน่าจะเป็นแบบผกผันเพื่อคาดการณ์เหตุการณ์ในอนาคตโดยอิงจากอดีต

แนวทางนี้ใช้ทฤษฎีบทเบย์ซึ่งอธิบายไว้ด้านล่าง:

ทฤษฎีบทของเบย์

สัจพจน์ของความน่าจะเป็นของ Renyi ตรวจสอบความน่าจะเป็นแบบมีเงื่อนไข โดยที่ความเป็นไปได้ของเหตุการณ์ A และเหตุการณ์ B ที่เกิดขึ้นนั้นขึ้นอยู่กับหรือมีเงื่อนไข ความน่าจะเป็นตามเงื่อนไขพื้นฐานสามารถเขียนได้ดังนี้:

ความน่าจะเป็นของเหตุการณ์ B ที่เกิดขึ้นนั้นขึ้นอยู่กับเหตุการณ์ A

สมการข้างต้นเป็นรากฐานของกฎเบย์ ซึ่งเป็นนิพจน์ทางคณิตศาสตร์ของทฤษฎีบทเบย์ที่ระบุว่า:

ในที่นี้ ∩ หมายถึงทางแยก

กฎของเบย์สามารถเขียนได้ดังนี้:

กฎ Bayes เป็นพื้นฐานของสถิติ Bayesian ซึ่งข้อมูลที่มีอยู่เกี่ยวกับพารามิเตอร์เฉพาะในแบบจำลองทางสถิติจะถูกเปรียบเทียบและอัปเดตด้วยข้อมูลที่รวบรวม

ความรู้เบื้องหลังจะแสดงเป็นการแจกแจงก่อนหน้า ซึ่งจะถูกเปรียบเทียบและศึกษากับข้อมูลที่สังเกตหรือเก็บรวบรวมเป็นฟังก์ชันความน่าจะเป็นที่จะหาการแจกแจงภายหลัง

การแจกแจงหลังนี้ใช้เพื่อคาดการณ์เหตุการณ์ในอนาคต

การประยุกต์ใช้แนวทางเบย์เซียนขึ้นอยู่กับพารามิเตอร์ต่อไปนี้:

1. การกำหนดรูปแบบก่อนหน้าและข้อมูล
2. การอนุมานที่เกี่ยวข้อง
3. กลั่นกรองและทำให้เพรียวลมโมเดล

โครงข่ายประสาทแบบเบย์คืออะไร?

Bayesian Neural Networks (BNN) คือเครือข่ายที่คุณสร้างขึ้นเมื่อคุณขยายเครือข่ายมาตรฐานโดยใช้วิธีการทางสถิติและปรับเปลี่ยนการอนุมานภายหลังเพื่อติดตามการโอเวอร์ฟิต เนื่องจากเป็นแนวทางแบบเบย์ จึงมีการแจกแจงความน่าจะเป็นที่เกี่ยวข้องกับพารามิเตอร์ของโครงข่ายประสาทเทียม

ใช้เพื่อแก้ปัญหาที่ซับซ้อนซึ่งไม่มีการไหลของข้อมูลอย่างอิสระ โครงข่ายประสาทแบบเบย์ช่วยควบคุมการใส่มากเกินไปในโดเมน เช่น อณูชีววิทยาและการวินิจฉัยทางการแพทย์

เราสามารถพิจารณาการกระจายคำตอบของคำถามทั้งหมดมากกว่าความเป็นไปได้เพียงครั้งเดียวโดยใช้โครงข่ายประสาทแบบเบย์ สิ่งเหล่านี้ช่วยคุณพิจารณาการเลือกรุ่น/การเปรียบเทียบและแก้ไขปัญหาที่เกี่ยวข้องกับการทำให้เป็นมาตรฐาน

สถิติแบบเบย์นำเสนอเครื่องมือทางคณิตศาสตร์ในการหาเหตุผลเข้าข้างตนเองและปรับปรุงความรู้เชิงอัตนัยเกี่ยวกับข้อมูลใหม่หรือหลักฐานทางวิทยาศาสตร์ ต่างจากวิธีการทางสถิติที่ใช้บ่อย ซึ่งทำงานโดยอาศัยสมมติฐานที่ว่าความน่าจะเป็นขึ้นอยู่กับความถี่ของเหตุการณ์ที่เกิดซ้ำภายใต้เงื่อนไขเดียวกัน

กล่าวโดยย่อ เทคนิค Bayesian เป็นการขยายสมมติฐานและความคิดเห็นของปัจเจกบุคคล ลักษณะสำคัญของแบบจำลองเบย์เซียนที่ทำให้มีประสิทธิภาพมากขึ้นคือการเข้าใจว่าบุคคลมีความคิดเห็นแตกต่างกันตามประเภทของข้อมูลที่ได้รับ

อย่างไรก็ตาม เมื่อมีหลักฐานและข้อมูลใหม่ปรากฏขึ้น บุคคลก็มีจุดบรรจบกัน นั่นคือ การ อนุมานแบบเบ ย์ การอัปเดตอย่างมีเหตุมีผลนี้เป็นคุณลักษณะพิเศษของสถิติแบบเบย์ที่ทำให้มีประสิทธิภาพในการวิเคราะห์ปัญหามากขึ้น

ในที่นี้ ความน่าจะเป็นของ 0 จะถูกนำไปใช้เมื่อไม่มีความหวังสำหรับเหตุการณ์ที่เกิดขึ้น และความน่าจะเป็นของ 1 จะถูกนำไปใช้เมื่อแน่ใจว่าเหตุการณ์นั้นจะเกิดขึ้น ความน่าจะเป็นระหว่าง 0 ถึง 1 ทำให้มีที่ว่างสำหรับผลลัพธ์ที่เป็นไปได้อื่นๆ

กฎของเบย์ถูกนำไปใช้เพื่อให้เกิดการอนุมานแบบเบย์เพื่อให้ได้การอนุมานที่ดีขึ้นจากแบบจำลอง

คุณใช้ Bayes Rule เพื่อรับการอนุมานแบบเบย์ได้อย่างไร

พิจารณาสมการ:

P(θ|D) = P(D|θ.)P(θ) / P(D)

P(θ) หมายถึงการแจกแจงก่อนหน้า

P(θ|D) หมายถึง ความเชื่อภายหลัง

P(D) แสดงถึงหลักฐาน

P(D|θ) บ่งบอกถึงความน่าจะเป็น

วัตถุประสงค์หลักของการอนุมานแบบเบย์คือการเสนอวิธีการที่มีเหตุผลและถูกต้องทางคณิตศาสตร์สำหรับการผสมผสานความเชื่อกับหลักฐานเพื่อให้ได้ความเชื่อที่อัปเดตภายหลัง ความเชื่อภายหลังสามารถใช้เป็นความเชื่อก่อนหน้าเมื่อมีการสร้างข้อมูลใหม่ ดังนั้น การอนุมานแบบเบย์ช่วยปรับปรุงความเชื่ออย่างต่อเนื่องด้วยความช่วยเหลือของกฎของเบส์

เมื่อพิจารณาจากตัวอย่างการพลิกเหรียญแบบเดียวกัน โมเดล Bayesian จะอัปเดตขั้นตอนจากเมื่อก่อนเป็นความเชื่อภายหลังด้วยการพลิกเหรียญแบบใหม่ วิธีแบบเบย์ให้ความน่าจะเป็นดังนี้

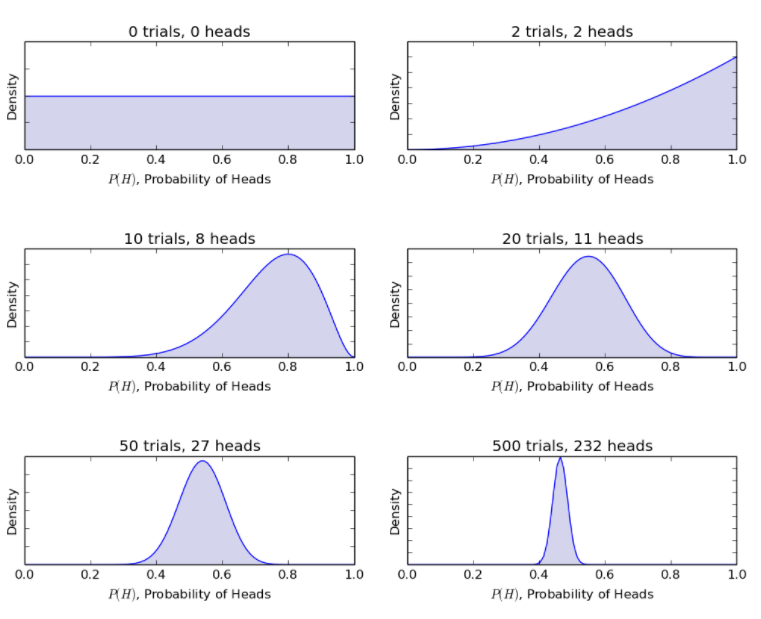
แหล่งที่มา

ดังนั้น แบบจำลองเบย์เซียนจึงทำให้สามารถหาเหตุผลเข้าข้างตนเองในสถานการณ์ที่ไม่แน่นอนด้วยข้อมูลที่จำกัดไปยังสถานการณ์จำลองที่กำหนดไว้มากขึ้นด้วยข้อมูลจำนวนมาก

ความแตกต่างที่โดดเด่นระหว่างแบบจำลองเบย์และแบบจำลองความถี่

สถิติประจำ

สถิติเบส์

เป้าหมายถือเป็นการประมาณการจุด และ CI

เป้าหมายถือเป็นการแจกแจงภายหลัง

ขั้นตอนเริ่มต้นจากการสังเกต

กระบวนการเริ่มต้นจากการแจกจ่ายครั้งก่อน

เมื่อใดก็ตามที่มีการสังเกตใหม่ วิธีการที่ใช้บ่อยจะคำนวณแบบจำลองที่มีอยู่ใหม่

เมื่อใดก็ตามที่มีการสังเกตใหม่ ๆ การกระจายส่วนหลัง ( อุดมการณ์ / สมมติฐาน) จะได้รับการปรับปรุง

ตัวอย่าง: การประมาณค่าค่าเฉลี่ย การทดสอบ t และ ANOVA

ตัวอย่าง: การประมาณค่าการกระจายหลังของค่าเฉลี่ยและการคาบเกี่ยวกันของช่วงความหนาแน่นสูง

ข้อดีของสถิติแบบเบย์

• เป็นวิธีการที่เป็นธรรมชาติและเรียบง่ายในการผสมผสานข้อมูลที่มีอยู่แล้วกับกรอบการทำงานที่มั่นคงพร้อมหลักฐานทางวิทยาศาสตร์ ข้อมูลในอดีตเกี่ยวกับพารามิเตอร์สามารถใช้เพื่อสร้างการแจกแจงก่อนหน้าสำหรับการตรวจสอบในอนาคต การอนุมานเป็นไปตามทฤษฎีบทเบย์
• การอนุมานจากแบบจำลองเบเซียนมีความถูกต้องทางตรรกะและทางคณิตศาสตร์ ไม่ใช่สมมติฐานคร่าวๆ ความแม่นยำยังคงที่โดยไม่คำนึงถึงขนาดของตัวอย่าง
• สถิติแบบเบย์เป็นไปตามหลักการความน่าจะเป็น เมื่อตัวอย่างที่แตกต่างกันสองตัวอย่างมีหน้าที่ความน่าจะเป็นร่วมกันสำหรับความเชื่อ θ การอนุมานทั้งหมดเกี่ยวกับความเชื่อควรมีความคล้ายคลึงกัน เทคนิคทางสถิติคลาสสิกไม่เป็นไปตามหลักการความน่าจะเป็น
• โซลูชันจากการวิเคราะห์แบบเบย์สามารถตีความได้อย่างง่ายดาย
• มีแพลตฟอร์มที่เอื้อต่อโมเดลต่างๆ เช่น โมเดลแบบลำดับชั้นและปัญหาข้อมูลที่ไม่สมบูรณ์ การคำนวณของโมเดลพาราเมตริกทั้งหมดสามารถติดตามได้โดยใช้เทคนิคตัวเลขอื่นๆ

การประยุกต์ใช้แบบจำลอง Bayesian ที่ประสบความสำเร็จในประวัติศาสตร์

วิธีการแบบเบย์มีการใช้งานที่ประสบความสำเร็จมากมายในช่วงสงครามโลกครั้งที่สอง บางส่วนของพวกเขามีการระบุไว้ด้านล่าง:

• นักสถิติชาวรัสเซีย Andrey Kolmogorov ประสบความสำเร็จในการใช้วิธีการแบบ Bayesian เพื่อปรับปรุงประสิทธิภาพของปืนใหญ่ของรัสเซีย
• โมเดลเบย์เซียนถูกใช้เพื่อทำลายรหัสของเรือ U ของเยอรมัน
• Bernard Koopman นักคณิตศาสตร์ชาวอเมริกันที่เกิดในฝรั่งเศส ช่วยพันธมิตรระบุตำแหน่งของเรือ U ของเยอรมันด้วยความช่วยเหลือของแบบจำลอง Bayesian เพื่อสกัดกั้นการส่งสัญญาณวิทยุ

หากคุณต้องการเรียนรู้เพิ่มเติมเกี่ยวกับสถิติแบบเบย์ นี่คือ การรับรองขั้นสูงของ upGrad ในการเรียนรู้ของเครื่องและระบบคลาวด์ เพื่อทำความเข้าใจแนวคิดพื้นฐานผ่านโครงการอุตสาหกรรมในชีวิตจริงและกรณีศึกษา หลักสูตร 12 เดือนเปิดสอนโดย IIT Madras และสนับสนุนการเรียนรู้ด้วยตนเอง

ติดต่อเราเพื่อขอรายละเอียดเพิ่มเติม