ทฤษฎีบทเบย์ในการเรียนรู้ของเครื่อง: บทนำ วิธีการใช้และตัวอย่าง
เผยแพร่แล้ว: 2021-02-04สารบัญ
บทนำ: ทฤษฎีบทเบย์คืออะไร?
ทฤษฎีบทเบย์ได้รับการตั้งชื่อตามนักคณิตศาสตร์ชาวอังกฤษ โธมัส เบย์ส์ ซึ่งทำงานอย่างกว้างขวางในทฤษฎีการตัดสินใจ ซึ่งเป็นสาขาวิชาคณิตศาสตร์ที่เกี่ยวข้องกับความน่าจะเป็น ทฤษฎีบทเบย์ยังใช้กันอย่างแพร่หลายในการเรียนรู้ของเครื่องด้วย ซึ่งเป็นวิธีที่ง่ายและมีประสิทธิภาพในการทำนายชั้นเรียนด้วยความแม่นยำและแม่นยำ วิธีการแบบเบย์ในการคำนวณความน่าจะเป็นแบบมีเงื่อนไขจะใช้ในแอปพลิเคชันการเรียนรู้ของเครื่องที่เกี่ยวข้องกับงานการจำแนกประเภท
เวอร์ชันที่เรียบง่ายของทฤษฎีบท Bayes หรือที่เรียกว่าการจำแนก Naive Bayes ใช้เพื่อลดเวลาและค่าใช้จ่ายในการคำนวณ ในบทความนี้ เราจะนำคุณผ่านแนวคิดเหล่านี้และอภิปรายเกี่ยวกับการประยุกต์ใช้ทฤษฎีบทเบย์ในการเรียนรู้ของเครื่อง
เข้าร่วม หลักสูตรแมชชีนเลิ ร์นนิง ออนไลน์จากมหาวิทยาลัยชั้นนำของโลก – ปริญญาโท, Executive Post Graduate Programme และ Advanced Certificate Program ใน ML & AI เพื่อติดตามอาชีพของคุณอย่างรวดเร็ว
เหตุใดจึงต้องใช้ทฤษฎีบทเบย์ในการเรียนรู้ของเครื่อง
ทฤษฎีบทเบย์เป็นวิธีการกำหนดความน่าจะเป็นแบบมีเงื่อนไข นั่นคือ ความน่าจะเป็นของเหตุการณ์หนึ่งเกิดขึ้นเนื่องจากอีกเหตุการณ์หนึ่งได้เกิดขึ้นแล้ว เนื่องจากความน่าจะเป็นแบบมีเงื่อนไขประกอบด้วยเงื่อนไขเพิ่มเติม กล่าวคือ มีข้อมูลที่มากขึ้น จึงสามารถนำไปสู่ผลลัพธ์ที่แม่นยำยิ่งขึ้น
ดังนั้น ความน่าจะเป็นแบบมีเงื่อนไขจึงเป็นสิ่งจำเป็นในการกำหนดการคาดการณ์และความน่าจะเป็นที่แม่นยำในการเรียนรู้ของเครื่อง เนื่องจากสาขานี้มีความแพร่หลายมากขึ้นในหลายโดเมน จึงเป็นสิ่งสำคัญที่จะต้องเข้าใจบทบาทของอัลกอริทึมและวิธีการ เช่น ทฤษฎีบทเบย์ในการเรียนรู้ของเครื่อง
ก่อนที่เราจะเข้าสู่ทฤษฎีบทนั้น เรามาทำความเข้าใจคำศัพท์ผ่านตัวอย่างกันก่อน สมมติว่าผู้จัดการร้านหนังสือมีข้อมูลเกี่ยวกับอายุและรายได้ของลูกค้า เขาต้องการทราบว่าการขายหนังสือมีการกระจายไปยังลูกค้าสามกลุ่มอายุ: เยาวชน (18-35) วัยกลางคน (35-60) และผู้สูงอายุ (60 ปีขึ้นไป)

ให้เราเรียกข้อมูลของเราว่า X ในคำศัพท์แบบเบย์ X เรียกว่าหลักฐาน เรามีสมมติฐาน H โดยที่เรามี X ที่เป็นของคลาส C ที่แน่นอน
เป้าหมายของเราคือกำหนดความน่าจะเป็นแบบมีเงื่อนไขของสมมติฐาน H ที่ให้ X เช่น P(H | X)
พูดง่ายๆ โดยหาค่า P(H | X) เราจะได้ความน่าจะเป็นของ X ที่อยู่ในคลาส C โดยที่ X X มีคุณลักษณะของอายุและรายได้ ตัวอย่างเช่น อายุ 26 ปีที่มีรายได้ 2,000 ดอลลาร์ H คือสมมติฐานของเราที่ลูกค้าจะซื้อหนังสือ
ใส่ใจกับเงื่อนไขสี่ข้อต่อไปนี้:
- หลักฐาน – ตามที่กล่าวไว้ก่อนหน้านี้ P(X) เรียกว่าหลักฐาน เป็นเพียงความน่าจะเป็นที่ลูกค้าจะ ในกรณีนี้ อายุ 26 ปี จะได้รับเงิน 2,000 ดอลลาร์
- ความน่าจะเป็นก่อนหน้า – P(H) หรือที่รู้จักในชื่อความน่าจะเป็นก่อนหน้า คือความน่าจะเป็นอย่างง่ายของสมมติฐานของเรา กล่าวคือลูกค้าจะซื้อหนังสือ ความน่าจะเป็นนี้จะไม่ได้รับการป้อนข้อมูลพิเศษใด ๆ ตามอายุและรายได้ เนื่องจากการคำนวณทำได้โดยใช้ข้อมูลน้อยกว่า ผลลัพธ์จึงแม่นยำน้อยลง
- ความน่าจะเป็นหลัง – P(H | X) เป็นที่รู้จักกันในชื่อความน่าจะเป็นภายหลัง โดยที่ P(H | X) คือความน่าจะเป็นที่ลูกค้าจะซื้อหนังสือ (H) โดยให้ X (ซึ่งเขาอายุ 26 ปีและมีรายได้ 2,000 ดอลลาร์)
- ความ น่าจะเป็น – P(X | H) คือความน่าจะเป็น ในกรณีนี้ เนื่องจากเรารู้ว่าลูกค้าจะซื้อหนังสือ ความน่าจะเป็นคือความน่าจะเป็นที่ลูกค้าอายุ 26 ปี และมีรายได้ 2,000 ดอลลาร์
ให้สิ่งเหล่านี้ ทฤษฎีบทเบย์กล่าวว่า:
P(H | X) = [ P(X | H) * P(H) ] / P(X)
สังเกตลักษณะที่ปรากฏของคำศัพท์สี่คำข้างต้นในทฤษฎีบท – ความน่าจะเป็นหลัง ความน่าจะเป็นที่น่าจะเป็น ความน่าจะเป็นก่อนหน้า และหลักฐาน
อ่าน: Naive Bayes อธิบาย
วิธีการใช้ทฤษฎีบทเบย์ในการเรียนรู้ของเครื่อง
Naive Bayes Classifier ซึ่งเป็นรุ่นที่เรียบง่ายของทฤษฎีบท Bayes ถูกใช้เป็นอัลกอริธึมการจำแนกประเภทเพื่อจำแนกข้อมูลออกเป็นคลาสต่างๆ ด้วยความแม่นยำและความเร็ว
เรามาดูกันว่า Naive Bayes Classifier สามารถใช้เป็นอัลกอริธึมการจัดหมวดหมู่ได้อย่างไร
- พิจารณาตัวอย่างทั่วไป: X เป็นเวกเตอร์ที่ประกอบด้วยแอตทริบิวต์ 'n' นั่นคือ X = {x1, x2, x3, …, xn}
- สมมติว่าเรามีคลาส 'm' {C1, C2, …, Cm} ลักษณนามของเราจะต้องทำนาย X เป็นของคลาสใดคลาสหนึ่ง ชั้นเรียนที่มีโอกาสเกิดภายหลังสูงสุดจะได้รับเลือกให้เป็นชั้นเรียนที่ดีที่สุด ดังนั้นในทางคณิตศาสตร์ ลักษณนามจะทำนายสำหรับคลาส Ci iff P(Ci | X) > P(Cj | X) การใช้ทฤษฎีบทเบย์:
P(Ci | X) = [ P(X | Ci) * P(Ci) ] / P(X)
- P(X) ไม่ขึ้นกับเงื่อนไข เป็นค่าคงที่สำหรับแต่ละคลาส ดังนั้นเพื่อเพิ่ม P(Ci | X) ให้ใหญ่สุด เราต้องขยายให้ใหญ่สุด [P(X | Ci) * P(Ci)] เมื่อพิจารณาว่าทุกคลาสมีโอกาสเท่ากัน เรามี P(C1) = P(C2) = P(C3) … = P(Cn) ท้ายที่สุด เราต้องเพิ่มค่า P(X | Ci) ให้สูงสุดเท่านั้น
- เนื่องจากชุดข้อมูลขนาดใหญ่ทั่วไปมีแนวโน้มที่จะมีหลายแอตทริบิวต์ จึงมีค่าใช้จ่ายในการคำนวณในการดำเนินการ P(X | Ci) สำหรับแต่ละแอตทริบิวต์ นี่คือจุดที่ความเป็นอิสระแบบมีเงื่อนไขระดับเข้ามาเพื่อลดความซับซ้อนของปัญหาและลดต้นทุนในการคำนวณ ด้วยความเป็นอิสระตามเงื่อนไขคลาส เราหมายความว่าเราถือว่าค่าของแอตทริบิวต์เป็นอิสระจากกันตามเงื่อนไข นี่คือการจำแนก Naive Bayes
P(Xi | C) = P(x1 | C) * P(x2 | C) *… * P(xn | C)
ตอนนี้ง่ายต่อการคำนวณความน่าจะเป็นที่น้อยกว่า สิ่งสำคัญประการหนึ่งที่ควรทราบที่นี่: เนื่องจาก xk เป็นของแต่ละแอตทริบิวต์ เราจึงต้องตรวจสอบว่าแอตทริบิวต์ที่เรากำลังดำเนินการอยู่นั้นเป็น หมวดหมู่ หรือ แบบ ต่อเนื่อง
- ถ้าเรามีคุณลักษณะที่เป็น หมวดหมู่ สิ่งต่างๆ จะง่ายขึ้น เราสามารถนับจำนวนอินสแตนซ์ของคลาส Ci ซึ่งประกอบด้วยค่า xk สำหรับแอตทริบิวต์ k แล้วหารด้วยจำนวนอินสแตนซ์ของคลาส Ci
- ถ้าเรามีแอตทริบิวต์แบบต่อเนื่อง เมื่อพิจารณาว่าเรามีฟังก์ชันการแจกแจงแบบปกติ เราจะใช้สูตรต่อไปนี้ โดยมีค่าเฉลี่ย ? และค่าเบี่ยงเบนมาตรฐาน ?:
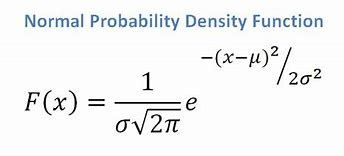

แหล่งที่มา
ในที่สุด เราก็จะได้ P(x | Ci) = F(xk, ?k, ?k)
- ตอนนี้ เรามีค่าทั้งหมดที่เราต้องใช้เพื่อใช้ทฤษฎีบทเบย์สำหรับแต่ละคลาส Ci คลาสที่คาดการณ์ไว้ของเราจะเป็นคลาสที่มีความเป็นไปได้สูงสุด P(X | Ci) * P(Ci)
ตัวอย่าง: การทำนายการจำแนกลูกค้าของร้านหนังสือ
เรามีชุดข้อมูลต่อไปนี้จากร้านหนังสือ:
| อายุ | รายได้ | นักเรียน | เครดิต_เรทติ้ง | Buys_Book |
| ความเยาว์ | สูง | ไม่ | ยุติธรรม | ไม่ |
| ความเยาว์ | สูง | ไม่ | ยอดเยี่ยม | ไม่ |
| วัยกลางคน | สูง | ไม่ | ยุติธรรม | ใช่ |
| อาวุโส | ปานกลาง | ไม่ | ยุติธรรม | ใช่ |
| อาวุโส | ต่ำ | ใช่ | ยุติธรรม | ใช่ |
| อาวุโส | ต่ำ | ใช่ | ยอดเยี่ยม | ไม่ |
| วัยกลางคน | ต่ำ | ใช่ | ยอดเยี่ยม | ใช่ |
| ความเยาว์ | ปานกลาง | ไม่ | ยุติธรรม | ไม่ |
| ความเยาว์ | ต่ำ | ใช่ | ยุติธรรม | ใช่ |
| อาวุโส | ปานกลาง | ใช่ | ยุติธรรม | ใช่ |
| ความเยาว์ | ปานกลาง | ใช่ | ยอดเยี่ยม | ใช่ |
| วัยกลางคน | ปานกลาง | ไม่ | ยอดเยี่ยม | ใช่ |
| วัยกลางคน | สูง | ใช่ | ยุติธรรม | ใช่ |
| อาวุโส | ปานกลาง | ไม่ | ยอดเยี่ยม | ไม่ |
เรามีคุณลักษณะต่างๆ เช่น อายุ รายได้ นักเรียน และอันดับเครดิต ชั้นเรียน buys_book ของเรามีสองผลลัพธ์: ใช่หรือไม่ใช่
เป้าหมายของเราคือการจัดประเภทตามคุณลักษณะต่อไปนี้:
X = {อายุ = เยาวชน นักเรียน = ใช่ รายได้ = ปานกลาง credit_rating = ยุติธรรม}
ดังที่เราแสดงให้เห็นก่อนหน้านี้ เพื่อเพิ่ม P(Ci | X) ให้สูงสุด เราจำเป็นต้องขยายให้ใหญ่สุด [ P(X | Ci) * P(Ci) ] สำหรับ i = 1 และ i = 2
ดังนั้น P(buys_book = ใช่) = 9/14 = 0.643
P(buys_book = ไม่) = 5/14 = 0.357
P(อายุ = เยาวชน | buys_book = ใช่) = 2/9 = 0.222
P(อายุ = เยาวชน | buys_book = ไม่) =3/5 = 0.60
P(รายได้ = ปานกลาง | buys_book = ใช่) = 4/9 = 0.444
P(รายได้ = ปานกลาง | buys_book = ไม่) = 2/5 = 0.400
P(นักเรียน = ใช่ | buys_book = ใช่) = 6/9 = 0.667
P(นักเรียน = ใช่ | buys_book = ไม่ใช่) = 1/5 = 0.200
P(credit_rating = ยุติธรรม | buys_book = ใช่) = 6/9 = 0.667
P(credit_rating = ยุติธรรม | buys_book = ไม่) = 2/5 = 0.400
โดยใช้ความน่าจะเป็นที่คำนวณไว้ข้างต้น เราได้
P(X | buys_book = ใช่) = 0.222 x 0.444 x 0.667 x 0.667 = 0.044
ในทำนองเดียวกัน
P(X | buys_book = ไม่) = 0.60 x 0.400 x 0.200 x 0.400 = 0.019
Ci ให้ P(X|Ci)*P(Ci) สูงสุดในระดับใด เราคำนวณ:
P(X | buys_book = ใช่)* P(buys_book = ใช่) = 0.044 x 0.643 = 0.028
P(X | buys_book = ไม่)* P(buys_book = ไม่ใช่) = 0.019 x 0.357 = 0.007

การเปรียบเทียบทั้งสองข้างต้น ตั้งแต่ 0.028 > 0.007 Naive Bayes Classifier คาดการณ์ว่าลูกค้าที่มีคุณสมบัติดังกล่าวข้างต้น จะ ซื้อหนังสือ
ชำระเงิน: แนวคิดและหัวข้อโครงการการเรียนรู้ของเครื่อง
Bayesian Classifier เป็นวิธีที่ดีหรือไม่?
อัลกอริธึมที่อิงตามทฤษฎีบทเบย์ในการเรียนรู้ด้วยเครื่องจะให้ผลลัพธ์ที่เทียบได้กับอัลกอริธึมอื่นๆ และตัวแยกประเภทแบบเบย์มักถือว่าเป็นวิธีการที่มีความแม่นยำสูงอย่างง่าย อย่างไรก็ตาม พึงระลึกไว้เสมอว่าตัวแยกประเภทแบบเบย์มีความเหมาะสมอย่างยิ่งในกรณีที่สมมติฐานของความเป็นอิสระแบบมีเงื่อนไขแบบมีเงื่อนไขนั้นถูกต้อง และไม่ครอบคลุมทุกกรณี ข้อกังวลในทางปฏิบัติอีกประการหนึ่งคือการได้รับข้อมูลความน่าจะเป็นทั้งหมดอาจไม่สามารถทำได้เสมอไป
บทสรุป
ทฤษฎีบทเบย์มีการใช้งานมากมายในการเรียนรู้ด้วยเครื่อง โดยเฉพาะในปัญหาตามการจำแนกประเภท การใช้อัลกอริทึมตระกูลนี้ในการเรียนรู้ของเครื่องเกี่ยวข้องกับความคุ้นเคยกับคำศัพท์ต่างๆ เช่น ความน่าจะเป็นก่อนหน้าและความน่าจะเป็นภายหลัง ในบทความนี้ เราได้พูดถึงพื้นฐานของทฤษฎีบทเบย์ การใช้ทฤษฎีนี้ในปัญหาการเรียนรู้ของเครื่อง และการทำงานโดยใช้ตัวอย่างการจัดหมวดหมู่
เนื่องจากทฤษฎีบท Bayes เป็นส่วนสำคัญของอัลกอริธึมตามการจัดหมวดหมู่ในการเรียนรู้ของเครื่อง คุณจึงสามารถเรียนรู้เพิ่มเติมเกี่ยวกับ โปรแกรมใบรับรองขั้นสูงของ upGrad ในการเรียนรู้ของเครื่องและ NLP ได้ หลักสูตรนี้จัดทำขึ้นโดยคำนึงถึงนักเรียนหลายประเภทที่สนใจแมชชีนเลิร์นนิง โดยเสนอการให้คำปรึกษาแบบ 1-1 และอีกมากมาย
เหตุใดเราจึงใช้ทฤษฎีบท Bayes ในการเรียนรู้ของเครื่อง
ทฤษฎีบทเบย์เป็นวิธีการคำนวณความน่าจะเป็นแบบมีเงื่อนไข หรือความน่าจะเป็นที่เหตุการณ์หนึ่งจะเกิดขึ้นหากมีเหตุการณ์อื่นเกิดขึ้นก่อนหน้านี้ ความน่าจะเป็นแบบมีเงื่อนไขสามารถนำไปสู่ผลลัพธ์ที่แม่นยำยิ่งขึ้นโดยการรวมเงื่อนไขเพิ่มเติม กล่าวคือ มีข้อมูลที่มากขึ้น เพื่อให้ได้ค่าประมาณและความน่าจะเป็นที่ถูกต้องในการเรียนรู้ของเครื่อง ต้องใช้ความน่าจะเป็นแบบมีเงื่อนไข ด้วยความแพร่หลายที่เพิ่มขึ้นของเขตข้อมูลในโดเมนที่หลากหลาย การเข้าใจถึงความสำคัญของอัลกอริธึมและแนวทางต่างๆ เช่น ทฤษฎีบทเบย์ในการเรียนรู้ของเครื่องจึงเป็นเรื่องสำคัญ
Bayesian Classifier เป็นตัวเลือกที่ดีหรือไม่?
ในการเรียนรู้ด้วยเครื่อง อัลกอริธึมที่อิงตามทฤษฎีบทเบย์จะให้ผลลัพธ์ที่เทียบได้กับวิธีการอื่นๆ และตัวแยกประเภทแบบเบย์ถือเป็นแนวทางที่มีความแม่นยำสูงอย่างง่าย อย่างไรก็ตาม สิ่งสำคัญที่ต้องจำไว้คือตัวแยกประเภทแบบเบย์จะใช้ได้ดีที่สุดเมื่อเงื่อนไขของความเป็นอิสระแบบมีเงื่อนไขของคลาสนั้นถูกต้อง ไม่ใช่ในทุกสถานการณ์ ข้อพิจารณาอีกประการหนึ่งคือการรับข้อมูลความน่าจะเป็นทั้งหมดอาจไม่สามารถทำได้เสมอไป
ทฤษฎีบทเบย์สามารถนำไปใช้ในทางปฏิบัติได้อย่างไร?
ทฤษฎีบทเบย์คำนวณความน่าจะเป็นที่จะเกิดขึ้นตามหลักฐานใหม่ที่เกี่ยวข้องหรืออาจเกี่ยวข้องกับมัน วิธีการนี้ยังสามารถใช้เพื่อดูว่าข้อมูลใหม่สมมุติฐานส่งผลต่อโอกาสของเหตุการณ์อย่างไร โดยสมมติว่าข้อมูลใหม่นั้นเป็นความจริง ยกตัวอย่างเช่น ไพ่ใบเดียวที่เลือกจากสำรับไพ่ 52 ใบ ความน่าจะเป็นที่ไพ่จะเป็นราชาคือ 4 หารด้วย 52 หรือ 1/13 หรือประมาณ 7.69 เปอร์เซ็นต์ โปรดทราบว่าสำรับประกอบด้วยสี่กษัตริย์ เอาเป็นว่าเปิดเผยว่าไพ่ที่เลือกเป็นไพ่หน้า เนื่องจากมีไพ่หน้า 12 ใบในสำรับ ความน่าจะเป็นที่ไพ่ที่เลือกจะเป็นราชาคือ 4 หารด้วย 12 หรือประมาณ 33.3 เปอร์เซ็นต์
